Nameless

PP Rocks

Team Members

1. Rene Anderson, researching RSA factorization
2. Francis Chau, researching on Image Processing, namely CImg
3. Yiqi Liu, Researching on DCRaw — a commonly used open source RAW image processing library

Email All

Progress

Assignment 1

Francis' discoveries

After doing some research and going through the trouble of building through windows command-line on the latest GNU compiler, I've managed to compile it.

I've downloaded and chose one of the sample projects that CImg carries, "tutorial.cpp" from http://cimg.eu/. Based on my observations through running it, it measures the amount of Red, Green and Blue values (RGB, primary colours) of a picture; there is one window displaying an image in this case a parrot and the other window to measure RGB values.

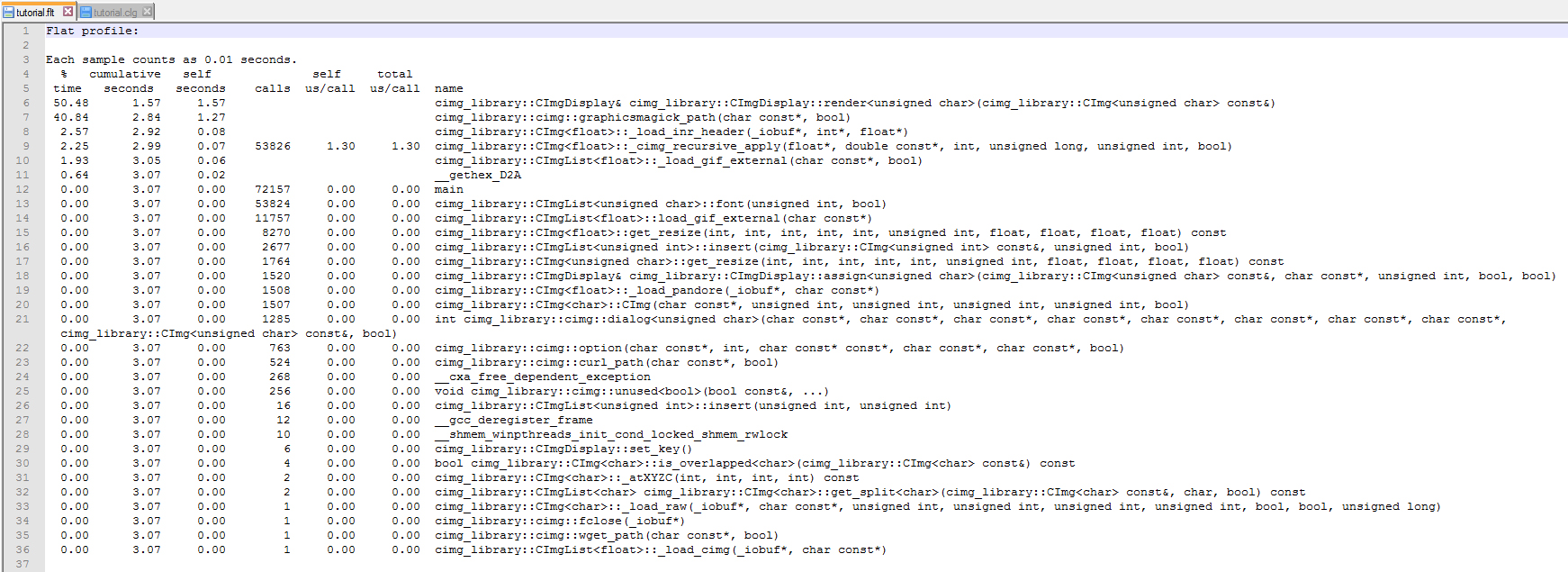
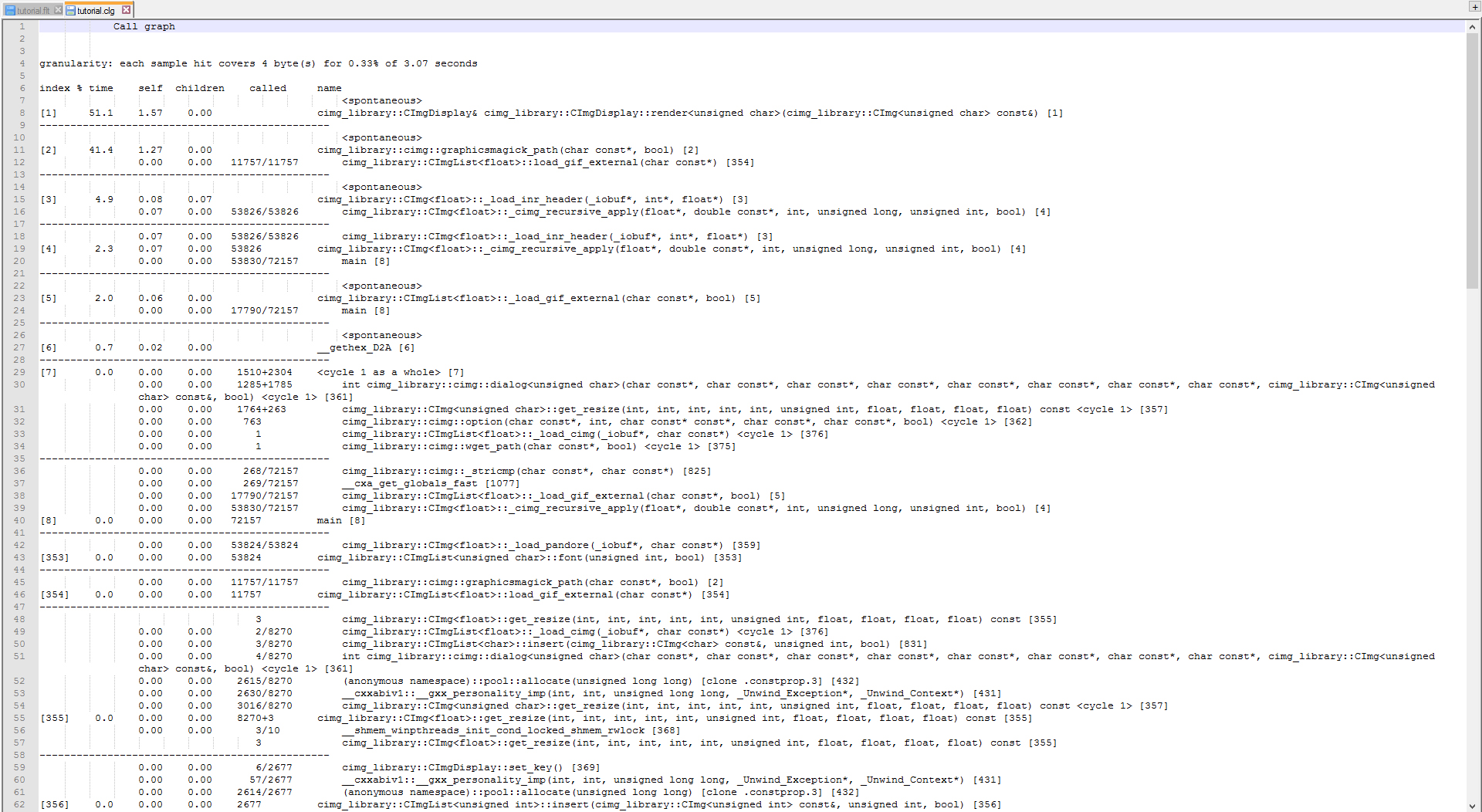
Performing some execution tests, I've found that CImgDisplay function consumes the most amount of time at 1.57 seconds.

Here's the flat diagram:

As well as the call graph diagram:

Yiqi's Findings

• The subject: RAW photo processing using the (commonly used) open source DCRaw library by Dave Coffin
• Library/program source file web page: https://www.cybercom.net/~dcoffin/dcraw/dcraw.c
• The script runProfile.sh in the submitted zip file executes the make command, run the profiling, and display the result
• Findings: the hot spot of the dcraw library is the ahd_interpolate() function, which contains large amount of loops, thus should be suitable of parallelization using GPU
• Although the time to process an individual image is not really long, for a batch of images, the time saving could be significant
• Here is the profiling result:

real    0m15.020s
user    0m13.653s
sys     0m1.016s

Flat profile:

Each sample counts as 0.01 seconds.
  %   cumulative   self              self     total
 time   seconds   seconds    calls  ms/call  ms/call  name
 30.34      3.68     3.68                             ahd_interpolate()
 26.71      6.92     3.24 45411856     0.00     0.00  cielab(unsigned short*, short*)
  9.40      8.06     1.14                             convert_to_rgb()
  8.74      9.12     1.06                             write_ppm_tiff()
  8.57     10.16     1.04                             lossless_jpeg_load_raw()
  4.29     10.68     0.52                             scale_colors()
  3.54     11.11     0.43                             crop_masked_pixels()
  3.22     11.50     0.39 23384000     0.00     0.00  getbithuff(int, unsigned short*)
  3.13     11.88     0.38     3950     0.10     0.24  ljpeg_row(int, jhead*)
  1.48     12.06     0.18 23384000     0.00     0.00  kodak_c603_load_raw()
  0.49     12.12     0.06                             pre_interpolate()
  0.08     12.13     0.01        1    10.00    10.00  border_interpolate(int)
  0.00     12.13     0.00       42     0.00     0.00  tiff_get(unsigned int, unsigned int*, unsigned int*, unsigned int*, unsigned int*)
  0.00     12.13     0.00       26     0.00     0.00  get2()
  0.00     12.13     0.00       26     0.00     0.00  get4()
  0.00     12.13     0.00        5     0.00     0.00  getreal(int)
  0.00     12.13     0.00        4     0.00     0.00  parse_tiff_ifd(int)
  0.00     12.13     0.00        3     0.00     0.00  parse_tiff(int)
  0.00     12.13     0.00        3     0.00     0.00  ljpeg_start(jhead*, int)
  0.00     12.13     0.00        2     0.00     0.00  make_decoder_ref(unsigned char const**)
  0.00     12.13     0.00        1     0.00     0.00  apply_tiff()
  0.00     12.13     0.00        1     0.00     0.00  parse_exif(int)
  0.00     12.13     0.00        1     0.00     0.00  adobe_coeff(char const*, char const*)
  0.00     12.13     0.00        1     0.00     0.00  cam_xyz_coeff(float (*) [4], double (*) [3])
  0.00     12.13     0.00        1     0.00     0.00  pseudoinverse(double (*) [3], double (*) [3], int)
  0.00     12.13     0.00        1     0.00     0.00  parse_makernote(int, int)
  0.00     12.13     0.00        1     0.00     0.00  parse_gps(int)

Rene's Findings

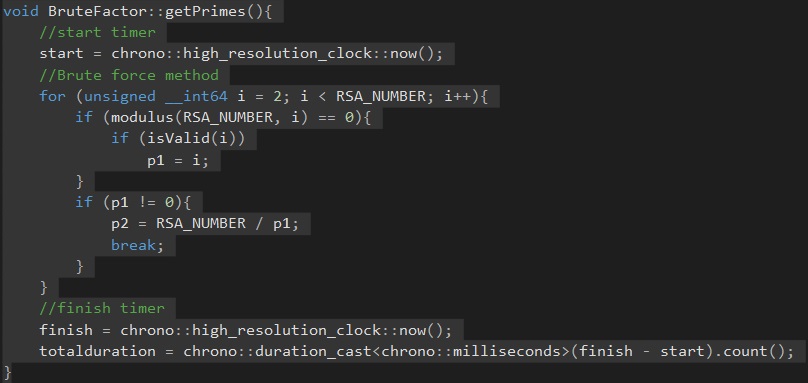
I decided to pursue an old project of mine RSA factorization. The old version was a simple brute force attack which I initially planned to parallelize because of the nature of this algorithm(Try every possible value starting from (1-->N). What changed my mind was that this brute force process was already reasonable for small prime numbers and would not see any noticeable gain, vs better algorithms, from this prallelization.

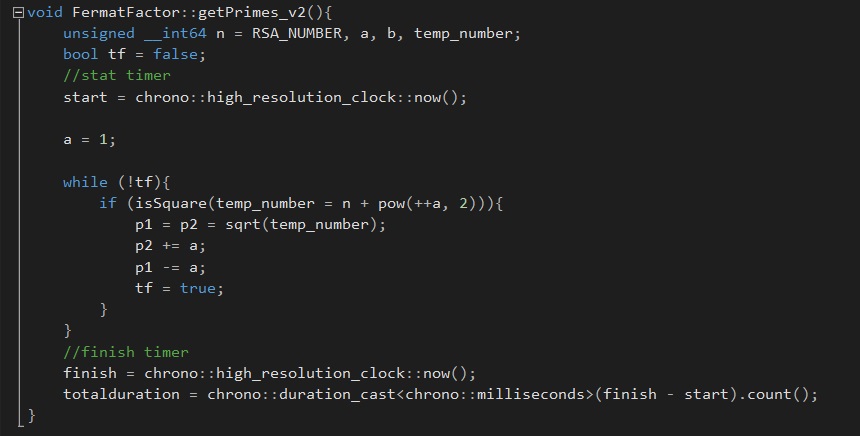
I decided to implement a new algorithm(Fermat factorization) and library(Mpir/GMP) to handle larger numbers >20 digits. The Fermat factorization algorithm worked fine for small numbers and numbers that had prime factors near it's roots. Problems arose when numbers >20 did not have prime factors near their roots and the algorithm failed to factor these(I assume because I eventually run out of memory after many hours of running). I looked at ways that this could be improved while also having the ability to be parallelized.

I found through research that the Quadratic sieve method would be a perfect candidate for this but unfortunately I am still in the process of understading the math behind it. What I did gather from this research is that the method to go about parallelizing it would have been:

1) collect a dictionary of possible factor candidates that can be factored easily by a given factor Base i.e. {2,3,5,7} .

2) Take the exponent values mod 2 of all the collected numbers' factor base and store them in a matrix. At this point CUDA could be used to process these matrices and solve them using Dixton's factorization method.

3) loading the result back to the host and processing the results.

Initial candidate for parallelization (Brute force):

Fermat factorization:

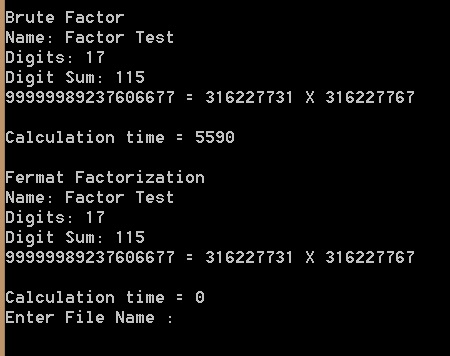
Brute force vs Fermat factorization: