Difference between revisions of "Ghost Cells"
(→Robert Subject: Multi Sampling Anti Aliasing) |
(→Tony) |
||
| Line 11: | Line 11: | ||
==== Tony ==== | ==== Tony ==== | ||
Subject: Jacobi's method for Poisson's equation | Subject: Jacobi's method for Poisson's equation | ||
| + | ===== Source Code ===== | ||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | ! poissan.h | ||
| + | |- | ||
| + | | | ||
| + | <source> | ||
| + | #ifndef POISSON_H | ||
| + | #define POISSON_H | ||
| + | #include <fstream> | ||
| + | |||
| + | namespace DPS{ | ||
| + | class Poisson { | ||
| + | size_t nRowsTotal; | ||
| + | size_t nColumns; | ||
| + | float* data; | ||
| + | int bufferSide; | ||
| + | |||
| + | void update (size_t startRow, size_t endRow, const float wx, const float wy); | ||
| + | void bufferSwitch(){ bufferSide = 1 - bufferSide; }; | ||
| + | |||
| + | public: | ||
| + | Poisson(std::ifstream& ifs); | ||
| + | Poisson(const size_t r, const size_t c, float* d); | ||
| + | ~Poisson(){ delete[] data; }; | ||
| + | float* operator()(const size_t iteration, const float wx, const float wy); | ||
| + | float* operator()(const size_t iteration){ | ||
| + | return operator()(iteration,0.1,0.1); | ||
| + | } | ||
| + | void show(std::ostream& ofs) const; | ||
| + | }; | ||
| + | } | ||
| + | #endif | ||
| + | |||
| + | </source> | ||
| + | |} | ||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | ! poissan.cpp | ||
| + | |- | ||
| + | | | ||
| + | <source> | ||
| + | #include <cstring> | ||
| + | #include <cstdlib> | ||
| + | #include <iomanip> | ||
| + | #include <iostream> | ||
| + | #include <string> | ||
| + | #include "poisson.h" | ||
| + | |||
| + | namespace DPS{ | ||
| + | Poisson::Poisson(std::ifstream& ifs){ | ||
| + | std::string line; | ||
| + | bufferSide = 0; | ||
| + | |||
| + | /* find number of columns */ | ||
| + | std::getline(ifs,line); | ||
| + | for (size_t i = 0 ; i < line.size() ; i++){ | ||
| + | if(line[i]==' ') nColumns++; | ||
| + | } | ||
| + | nColumns++; | ||
| + | |||
| + | /* find number of rows */ | ||
| + | nRowsTotal++; /* already fetched one */ | ||
| + | while(std::getline(ifs,line)) | ||
| + | nRowsTotal++; | ||
| + | ifs.clear(); | ||
| + | |||
| + | try{ | ||
| + | data = new float[nColumns * nRowsTotal * 2]; | ||
| + | } | ||
| + | catch (...){ | ||
| + | throw std::runtime_error("Failed to Allocate Memory"); | ||
| + | } | ||
| + | |||
| + | /* readin data */ | ||
| + | ifs.seekg(0,ifs.beg); | ||
| + | std::cout << ifs.tellg() << std::endl; | ||
| + | for (size_t i = 0 ; i < nRowsTotal * nColumns ; i++) { | ||
| + | ifs >> data[i]; | ||
| + | } | ||
| + | |||
| + | std::memset(data+nRowsTotal*nColumns,0,nRowsTotal*nColumns*sizeof(float)); | ||
| + | } | ||
| + | |||
| + | Poisson::Poisson(const size_t r, const size_t c, float* d){ | ||
| + | bufferSide = 0; | ||
| + | nRowsTotal = r; | ||
| + | nColumns = c; | ||
| + | try{ | ||
| + | data = new float[r*c*2]; | ||
| + | } | ||
| + | catch (...){ | ||
| + | throw std::runtime_error("Failed to Allocate Memory"); | ||
| + | } | ||
| + | std::memcpy(data,d,r*c*sizeof(float)); | ||
| + | std::memset(data+r*c,0,r*c*sizeof(float)); | ||
| + | } | ||
| + | |||
| + | void Poisson::update (size_t startRow, size_t endRow, const float wx, const float wy){ | ||
| + | float* x_new = data + (1-bufferSide)*nRowsTotal*nColumns; | ||
| + | float* x_old = data + bufferSide*nRowsTotal*nColumns; | ||
| + | for (size_t i = startRow; i <= endRow; i++) | ||
| + | for (size_t j = 1; j < nColumns - 1; j++) | ||
| + | x_new[i * nColumns + j] = x_old[i * nColumns + j] | ||
| + | + wx * (x_old[(i + 1) * nColumns + j] + x_old[(i - 1) * nColumns + j] | ||
| + | - 2.0f * x_old[i * nColumns + j]) | ||
| + | + wy * (x_old[i * nColumns + j + 1] + x_old[i * nColumns + j - 1] | ||
| + | - 2.0f * x_old[i * nColumns + j]); | ||
| + | } | ||
| + | |||
| + | float* Poisson::operator()(const size_t nIterations, const float wx, const float wy){ | ||
| + | for (size_t i = 0; i < nIterations; i++) { | ||
| + | update(0, nRowsTotal-1, wx, wy); | ||
| + | bufferSwitch(); | ||
| + | } | ||
| + | return data; | ||
| + | } | ||
| + | |||
| + | void Poisson::show(std::ostream& ofs) const{ | ||
| + | ofs << std::fixed << std::setprecision(1); | ||
| + | for (size_t j = 0; j < nColumns ; j++) { | ||
| + | for (size_t i = 0 ; i < nRowsTotal ; i++) | ||
| + | ofs << std::setw(8) << data[ bufferSide*nColumns*nRowsTotal + i * nColumns + j]; | ||
| + | ofs << std::endl; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | </source> | ||
| + | |} | ||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | ! main.cpp | ||
| + | |- | ||
| + | | | ||
| + | <source> | ||
| + | // based on code from LLNL tutorial mpi_heat2d.c | ||
| + | // Master-Worker Programming Model | ||
| + | // Chris Szalwinski - 2018/11/13 | ||
| + | // Adopted by Tony Sim - 2019/02/16 | ||
| + | #include <iostream> | ||
| + | #include <fstream> | ||
| + | #include <iomanip> | ||
| + | #include <cstdlib> | ||
| + | #include <stdexcept> | ||
| + | |||
| + | #include "poisson.h" | ||
| + | |||
| + | // solution constants | ||
| + | const size_t NONE = 0; | ||
| + | const size_t MINPARTITIONS = 1; | ||
| + | const size_t MAXPARTITIONS = 7; | ||
| + | // weights | ||
| + | const float wx = 0.1f; | ||
| + | const float wy = 0.1f; | ||
| + | |||
| + | int main(int argc, char** argv) { | ||
| + | if (argc != 4) { | ||
| + | std::cerr << "*** Incorrect number of arguments ***\n"; | ||
| + | std::cerr << "Usage: " << argv[0] | ||
| + | << " input_file output_file no_of_iterations\n"; | ||
| + | return 1; | ||
| + | } | ||
| + | |||
| + | std::ifstream input(argv[1]); | ||
| + | std::ofstream output(argv[2]); | ||
| + | std::ofstream temp("init.csv"); | ||
| + | |||
| + | if(!input.is_open()){ | ||
| + | std::cerr << "Invalid Input File" << std::endl; | ||
| + | return 2; | ||
| + | } | ||
| + | if(!output.is_open()){ | ||
| + | std::cerr << "Invalid Output File" << std::endl; | ||
| + | return 2; | ||
| + | } | ||
| + | |||
| + | DPS::Poisson* p = nullptr; | ||
| + | try{ | ||
| + | p = new DPS::Poisson(input); | ||
| + | } | ||
| + | catch(std::exception& e){ | ||
| + | std::cerr << "Error: " << e.what() << std::endl; | ||
| + | } | ||
| + | |||
| + | p->show(temp); | ||
| + | |||
| + | size_t nIterations = std::atoi(argv[3]); | ||
| + | |||
| + | (*p)(nIterations); | ||
| + | |||
| + | // write results to file | ||
| + | p->show(output); | ||
| + | |||
| + | delete p; | ||
| + | |||
| + | } | ||
| + | |||
| + | </source> | ||
| + | |} | ||
| + | ===== Introduction ===== | ||
| + | The presented code simulates heat map using Jacobi's method for Poisson's equation. It is represented in a 2D array, and each element updates its value based on the adjacent elements at a given moment. Each iteration represent one instance in time. By repeating the calculation over the entire array through multiple iterations, we can estimate the state of the heat transfer after a given time interval. | ||
| + | |||
| + | ===== Profiling ===== | ||
| + | The profiling was conducted using a data set of 79 rows and 205 columns over 150000 iterations. | ||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | ! Flat profile | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | Flat profile: | ||
| + | |||
| + | Each sample counts as 0.01 seconds. | ||
| + | % cumulative self self total | ||
| + | time seconds seconds calls us/call us/call name | ||
| + | 98.57 2.75 2.75 150000 18.33 18.33 DPS::Poisson::update(unsigned long, unsigned long, float, float) | ||
| + | 0.00 2.75 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN3DPS7PoissonC2ERSt14basic_ifstreamIcSt11char_traitsIcEE | ||
| + | 0.00 2.75 0.00 1 0.00 0.00 _GLOBAL__sub_I_main | ||
| + | |||
| + | |||
| + | |} | ||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | ! Call graph | ||
| + | |- | ||
| + | | | ||
| + | Call graph | ||
| + | |||
| + | |||
| + | granularity: each sample hit covers 2 byte(s) for 0.36% of 2.75 seconds | ||
| + | |||
| + | index % time self children called name | ||
| + | 2.75 0.00 150000/150000 DPS::Poisson::operator()(unsigned long, float, float) [2] | ||
| + | [1] 100.0 2.75 0.00 150000 DPS::Poisson::update(unsigned long, unsigned long, float, float) [1] | ||
| + | ----------------------------------------------- | ||
| + | <spontaneous> | ||
| + | [2] 100.0 0.00 2.75 DPS::Poisson::operator()(unsigned long, float, float) [2] | ||
| + | 2.75 0.00 150000/150000 DPS::Poisson::update(unsigned long, unsigned long, float, float) [1] | ||
| + | ----------------------------------------------- | ||
| + | 0.00 0.00 1/1 __libc_csu_init [21] | ||
| + | [10] 0.0 0.00 0.00 1 _GLOBAL__sub_I__ZN3DPS7PoissonC2ERSt14basic_ifstreamIcSt11char_traitsIcEE [10] | ||
| + | ----------------------------------------------- | ||
| + | 0.00 0.00 1/1 __libc_csu_init [21] | ||
| + | [11] 0.0 0.00 0.00 1 _GLOBAL__sub_I_main [11] | ||
| + | ----------------------------------------------- | ||
| + | |||
| + | |||
| + | Index by function name | ||
| + | |||
| + | [10] _GLOBAL__sub_I__ZN3DPS7PoissonC2ERSt14basic_ifstreamIcSt11char_traitsIcEE (poisson.cpp) [11] _GLOBAL__sub_I_main (main.cpp) [1] DPS::Poisson::update(unsigned long, unsigned long, float, float) | ||
| + | |||
| + | |||
| + | |} | ||
| + | |||
| + | =====Analysis===== | ||
| + | given 98.57 percent of time is spent on the update() function, it is considered the hotspot. | ||
| + | Total time taken was 2.75. | ||
| + | |||
| + | If we consider a GPU environment with 1000 cores, we can estimate the following speedup: | ||
| + | S1000 = 1/(1-.9857 + .9857/1000) = 65.00 | ||
| + | In fact, the speed will decrease from 2.75 seconds to 0.0450 seconds. | ||
| + | |||
==== Robert ==== | ==== Robert ==== | ||
===== Multi Sampling Anti Aliasing ===== | ===== Multi Sampling Anti Aliasing ===== | ||
Revision as of 05:00, 17 February 2019
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
[hide]Ghost Cells
Team Members
- Tony Sim, Issue Dumper
- Robert Dittrich, Issue Collector
- Inna Zhogova, Issue Resolver
Progress
Assignment 1
Tony
Subject: Jacobi's method for Poisson's equation
Source Code
| [Expand] poissan.h |
|---|
| [Expand] poissan.cpp |
|---|
| [Expand] main.cpp |
|---|
Introduction
The presented code simulates heat map using Jacobi's method for Poisson's equation. It is represented in a 2D array, and each element updates its value based on the adjacent elements at a given moment. Each iteration represent one instance in time. By repeating the calculation over the entire array through multiple iterations, we can estimate the state of the heat transfer after a given time interval.
Profiling
The profiling was conducted using a data set of 79 rows and 205 columns over 150000 iterations.
| [Expand] Flat profile |
|---|
| [Expand] Call graph |
|---|
Analysis
given 98.57 percent of time is spent on the update() function, it is considered the hotspot. Total time taken was 2.75.
If we consider a GPU environment with 1000 cores, we can estimate the following speedup: S1000 = 1/(1-.9857 + .9857/1000) = 65.00 In fact, the speed will decrease from 2.75 seconds to 0.0450 seconds.
Robert
Multi Sampling Anti Aliasing
Source Files
| [Expand] main.cpp |
|---|
| [Expand] vec3.h |
|---|
Introduction
For my selection I chose to do Anti Aliasing since I see it a lot in video games but I never really knew how it worked. There are other anti aliasing methods like FXAA which is fast approximate anti aliasing but it seemed a lot more complicated than MSAA. The way I approached this problem is by getting the color of the pixels around a pixel. In you can specify the distance it will search in the application flags. In my implementation you specify an input file, output file, the radius of pixels to sample and how many passes to take on the image. In my tests the command line options I used was an image I made in paint with 4 sample size and 4 passes.
| [Expand] Before |
|---|
| [Expand] After |
|---|
Profiling
| [Expand] Profiling |
|---|
Conclusion
Since the msaa function I wrote is a hotspot of the program I would suggest offloading part of it to a GPU, more specifically the part that finds the average of colors of the nearby pixels. That part also does not depend on previous iterations to finish so it is a prime candidate for parallelization.
Inna
Subject: Data compression - LWZ algorithm.
Source: http://www.cplusplus.com/articles/iL18T05o/#Version1
I tested the following source code for a compression and decompression of .txt files and a gif.
| [Expand] lwz.cpp( ... ) |
|---|
Tested data
1. book.txt - a 343 kilobyte text file.
2. words.txt - a 4.7 megabyte text file.
3. fire.gif - a 309 kilobyte graphical image.
Flat Profiles
Book
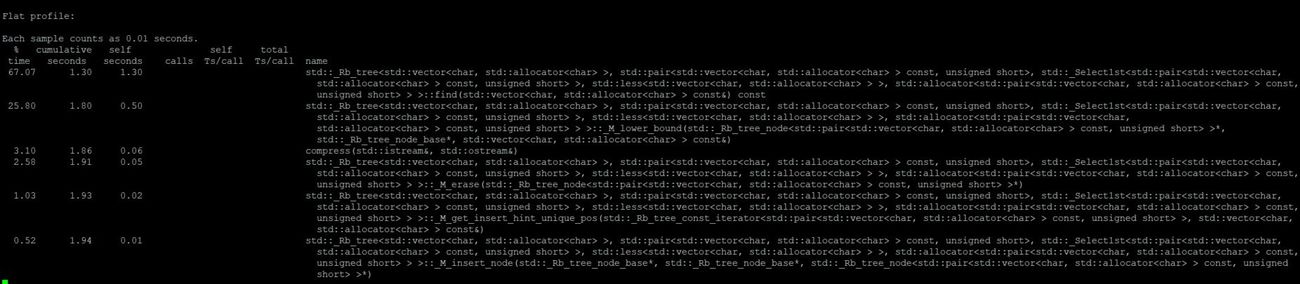
Flat profile for compression:
Flat profile for decompression:
Text
Flat profile for compression:
Flat profile for decompression:
GIF
Flat profile for compression:
Flat profile for decompression: