TriForce
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
[hide]TriForce
Team Members
- David Ferri, Sudoku Solver
- Vincent Terpstra, Julia Sets
- Raymond Kiguru, EasyBMP
Progress
Assignment 1: Sudoku Solver
Sudoku Solver Profiling
Rather than try to continuously increase the difficulty of a 9x9 sudoku, I decided to modify the program I found to handle larger and large sudokus, increasing the size of the matrices that make up the sudoku (starting with a 9x9 sudoku, which is 9 3x3 matrices, then 16x16 which is 16 4x4 matrices, and finally 25x25 which is 25 5x5 matrices) without changing the logic of the program (only constants), so larger sudokus are solved the same way as a normal one.
Source code from: https://www.geeksforgeeks.org/sudoku-backtracking-7/
| [Expand] Original Code: |
|---|
Obtaining flat profiles and call graphs on matrix environment:
$ g++ sudokuC.cpp -std=c++0x -o Sudoku $ ./Sudoku 3 1 6 5 7 8 4 9 2 5 2 9 1 3 4 7 6 8 4 8 7 6 2 9 5 3 1 2 6 3 4 1 5 9 8 7 9 7 4 8 6 3 1 2 5 8 5 1 7 9 2 6 4 3 1 3 8 9 4 7 2 5 6 6 9 2 3 5 1 8 7 4 7 4 5 2 8 6 3 1 9 $ gprof -p -b ./Sudoku gmon.out > 9x9.flt $ gprof -q -b ./Sudoku gmon.out > 9x9.clg
$ g++ sudokuC16.cpp -std=c++0x -pg -o Sudoku16 $ ./Sudoku16 12 8 6 516 1 2 31314 410 9 71115 11 915131210 7 5 2 6 816 414 1 3 4 316 71514 813 91211 1 6 5 210 114 210 911 4 615 3 5 7 8131216 16 6 415 5 213 7 1 910 811 31412 511 9 2 4 312151416 613 7 110 8 1012 3 8 1 61114 4 5 7 216 91513 13 1 714 8 91016 3111215 2 4 5 6 2 71316 6 4 51211 8 9141015 3 1 6 411 914 7 3 210 1151213 816 5 141510 11113 9 8 5 416 312 2 6 7 3 5 812101516 1 7 213 61411 4 9 7 2 5 313121411 610 1 91516 8 4 91014 6 7 8 1 41615 2 5 3121311 813 1 4 216151012 7 311 5 6 914 15161211 3 5 6 9 81314 4 110 7 2 $ gprof -p -b ./Sudoku16 gmon.out > 16x16.flt $ gprof -q -b ./Sudoku16 gmon.out > 16x16.clg
$ g++ sudokuC25.cpp -std=c++0x -pg -o Sudoku25 $ ./Sudoku25 111 42025241915171021 8181422 612 9 316 2 71323 5 5 2192324 82212 9 316 6 7201718212514131011 4 115 1714 9 6 32521 5 7201110 2 113 4 82423151812162219 16 721 818 4 2131123 51915241210201722 1 9 62514 3 101315122214 118 61623 925 4 3 7 51911 2 824202117 12 11110 6 513232415 716 817212519 3 4 92214 22018 8191321 916 42512 215 3 511201417231822 110 724 6 4171418 7 9 322211925 124 223 5132010 61615 81112 22 3241523182011 1 71013 4 61416 21221 8 5191725 9 2016 225 510 8 61417 922121819 11115 724 3232113 4 1325 3 510 22314 418221517192420 7 1 9211216 6 811 1423 124121916 815 6 2 7202510 3 413171121 9 51822 7 818111720242122 9 3 4 11216 2 61419 52513151023 22216 9211711 71025 8 51413 6122418152319 4 1 320 6152019 41312 3 5 118112321 9 822162510 71724 214 211812 216 71019 313 12422 9 41115 6201417 823 525 924 813 1 625 420121714 3 718231622 51911211015 2 231022 71521 5 91814 62016 81117 1 21325 4 3191224 25 5 61411 117 2 8241321192315 9 31012 420182216 7 32017 4192215162311122510 5 22118 824 7 6 114 913 19 62322 81518 125 414 2 9 3 7131011162024 5121721 15 4 51714 3 72419 8202311102522 921 11213 218 616 1112 7162023 617 22124181315 11925 5 8 31422 9 410 18 925 1 21114101322 4122116 52423 7 6171520 319 8 242110 31312 92016 51917 622 81514 4 218232511 7 1 $ gprof -p -b ./Sudoku25 gmon.out > 25x25.flt $ gprof -q -b ./Sudoku25 gmon.out > 25x25.clg
For 9x9 Sudoku Puzzle (3x3 squares)
Flat profile: Each sample counts as 0.01 seconds. no time accumulated % cumulative self self total time seconds seconds calls Ts/call Ts/call name 0.00 0.00 0.00 6732 0.00 0.00 isSafe(int (*) [9], int, int, int) 0.00 0.00 0.00 6732 0.00 0.00 UsedInRow(int (*) [9], int, int) 0.00 0.00 0.00 2185 0.00 0.00 UsedInCol(int (*) [9], int, int) 0.00 0.00 0.00 1078 0.00 0.00 UsedInBox(int (*) [9], int, int, int) 0.00 0.00 0.00 770 0.00 0.00 FindUnassignedLocation(int (*) [9], int&, int&) 0.00 0.00 0.00 1 0.00 0.00 SolveSudoku(int (*) [9]) 0.00 0.00 0.00 1 0.00 0.00 printGrid(int (*) [9])
Call graph
granularity: each sample hit covers 2 byte(s) no time propagated
index % time self children called name
0.00 0.00 6732/6732 SolveSudoku(int (*) [9]) [13]
[8] 0.0 0.00 0.00 6732 isSafe(int (*) [9], int, int, int) [8]
0.00 0.00 6732/6732 UsedInRow(int (*) [9], int, int) [9]
0.00 0.00 2185/2185 UsedInCol(int (*) [9], int, int) [10]
0.00 0.00 1078/1078 UsedInBox(int (*) [9], int, int, int) [11]
-----------------------------------------------
0.00 0.00 6732/6732 isSafe(int (*) [9], int, int, int) [8]
[9] 0.0 0.00 0.00 6732 UsedInRow(int (*) [9], int, int) [9]
-----------------------------------------------
0.00 0.00 2185/2185 isSafe(int (*) [9], int, int, int) [8]
[10] 0.0 0.00 0.00 2185 UsedInCol(int (*) [9], int, int) [10]
-----------------------------------------------
0.00 0.00 1078/1078 isSafe(int (*) [9], int, int, int) [8]
[11] 0.0 0.00 0.00 1078 UsedInBox(int (*) [9], int, int, int) [11]
-----------------------------------------------
0.00 0.00 770/770 SolveSudoku(int (*) [9]) [13]
[12] 0.0 0.00 0.00 770 FindUnassignedLocation(int (*) [9], int&, int&) [12]
-----------------------------------------------
769 SolveSudoku(int (*) [9]) [13]
0.00 0.00 1/1 main [6]
[13] 0.0 0.00 0.00 1+769 SolveSudoku(int (*) [9]) [13]
0.00 0.00 6732/6732 isSafe(int (*) [9], int, int, int) [8]
0.00 0.00 770/770 FindUnassignedLocation(int (*) [9], int&, int&) [12]
769 SolveSudoku(int (*) [9]) [13]
-----------------------------------------------
0.00 0.00 1/1 main [6]
[14] 0.0 0.00 0.00 1 printGrid(int (*) [9]) [14]
-----------------------------------------------
Index by function name
[13] SolveSudoku(int (*) [9]) [11] UsedInBox(int (*) [9], int, int, int) [14] printGrid(int (*) [9])
[12] FindUnassignedLocation(int (*) [9], int&, int&) [10] UsedInCol(int (*) [9], int, int)
[8] isSafe(int (*) [9], int, int, int) [9] UsedInRow(int (*) [9], int, int)
For 16x16 Sudoku Puzzle (4x4 squares)
Puzzle from: [1]
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 39.04 15.00 15.00 28071636 0.00 0.00 FindUnassignedLocation(int (*) [16], int&, int&) 36.19 28.90 13.90 449145092 0.00 0.00 UsedInRow(int (*) [16], int, int) 10.60 32.97 4.07 120354547 0.00 0.00 UsedInCol(int (*) [16], int, int) 4.97 34.88 1.91 41212484 0.00 0.00 UsedInBox(int (*) [16], int, int, int) 4.59 36.65 1.76 1 1.76 38.39 SolveSudoku(int (*) [16]) 4.55 38.39 1.75 449145092 0.00 0.00 isSafe(int (*) [16], int, int, int) 0.01 38.40 0.01 frame_dummy 0.00 38.40 0.00 1 0.00 0.00 printGrid(int (*) [16])
Call graph
granularity: each sample hit covers 2 byte(s) for 0.03% of 36.85 seconds
index % time self children called name
<spontaneous>
[1] 100.0 0.00 36.85 main [1]
1.93 34.93 1/1 SolveSudoku(int (*) [16]) [2]
0.00 0.00 1/1 printGrid(int (*) [16]) [14]
-----------------------------------------------
28071635 SolveSudoku(int (*) [16]) [2]
1.93 34.93 1/1 main [1]
[2] 100.0 1.93 34.93 1+28071635 SolveSudoku(int (*) [16]) [2]
1.69 19.09 449145092/449145092 isSafe(int (*) [16], int, int, int) [3]
14.14 0.00 28071636/28071636 FindUnassignedLocation(int (*) [16], int&, int&) [4]
28071635 SolveSudoku(int (*) [16]) [2]
-----------------------------------------------
1.69 19.09 449145092/449145092 SolveSudoku(int (*) [16]) [2]
[3] 56.4 1.69 19.09 449145092 isSafe(int (*) [16], int, int, int) [3]
13.58 0.00 449145092/449145092 UsedInRow(int (*) [16], int, int) [5]
3.54 0.00 120354547/120354547 UsedInCol(int (*) [16], int, int) [6]
1.98 0.00 41212484/41212484 UsedInBox(int (*) [16], int, int, int) [7]
-----------------------------------------------
14.14 0.00 28071636/28071636 SolveSudoku(int (*) [16]) [2]
[4] 38.4 14.14 0.00 28071636 FindUnassignedLocation(int (*) [16], int&, int&) [4]
-----------------------------------------------
13.58 0.00 449145092/449145092 isSafe(int (*) [16], int, int, int) [3]
[5] 36.8 13.58 0.00 449145092 UsedInRow(int (*) [16], int, int) [5]
-----------------------------------------------
3.54 0.00 120354547/120354547 isSafe(int (*) [16], int, int, int) [3]
[6] 9.6 3.54 0.00 120354547 UsedInCol(int (*) [16], int, int) [6]
-----------------------------------------------
1.98 0.00 41212484/41212484 isSafe(int (*) [16], int, int, int) [3]
[7] 5.4 1.98 0.00 41212484 UsedInBox(int (*) [16], int, int, int) [7]
-----------------------------------------------
0.00 0.00 1/1 main [1]
[14] 0.0 0.00 0.00 1 printGrid(int (*) [16]) [14]
-----------------------------------------------
Index by function name
[2] SolveSudoku(int (*) [16]) [7] UsedInBox(int (*) [16], int, int, int) [14] printGrid(int (*) [16])
[4] FindUnassignedLocation(int (*) [16], int&, int&) [6] UsedInCol(int (*) [16], int, int)
[3] isSafe(int (*) [16], int, int, int) [5] UsedInRow(int (*) [16], int, int)
For 25x25 Sudoku Puzzle (5x5 squares) Puzzle from: http://www.sudoku-download.net/sudoku_25x25.php
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ks/call Ks/call name 48.76 1052.18 1052.18 425478951 0.00 0.00 UsedInRow(int (*) [25], int, int) 25.24 1596.81 544.63 876012758 0.00 0.00 FindUnassignedLocation(int (*) [25], int&, int&) 12.48 1866.03 269.21 590817023 0.00 0.00 UsedInCol(int (*) [25], int, int) 4.83 1970.24 104.21 425478951 0.00 0.00 isSafe(int (*) [25], int, int, int) 4.79 2073.51 103.27 1 0.10 2.17 SolveSudoku(int (*) [25]) 4.35 2167.39 93.89 1355081265 0.00 0.00 UsedInBox(int (*) [25], int, int, int) 0.01 2167.56 0.17 frame_dummy 0.00 2167.56 0.00 1 0.00 0.00 printGrid(int (*) [25])
Call graph
granularity: each sample hit covers 2 byte(s) for 0.00% of 2085.44 seconds
index % time self children called name
<spontaneous>
[1] 100.0 0.00 2085.30 main [1]
97.03 1988.27 1/1 SolveSudoku(int (*) [25]) [2]
0.00 0.00 1/1 printGrid(int (*) [25]) [14]
-----------------------------------------------
876012757 SolveSudoku(int (*) [25]) [2]
97.03 1988.27 1/1 main [1]
[2] 100.0 97.03 1988.27 1+876012757 SolveSudoku(int (*) [25]) [2]
101.19 1361.55 425478951/425478951 isSafe(int (*) [25], int, int, int) [3]
525.53 0.00 876012758/876012758 FindUnassignedLocation(int (*) [25], int&, int&) [5]
876012757 SolveSudoku(int (*) [25]) [2]
-----------------------------------------------
101.19 1361.55 425478951/425478951 SolveSudoku(int (*) [25]) [2]
[3] 70.1 101.19 1361.55 425478951 isSafe(int (*) [25], int, int, int) [3]
1011.03 0.00 425478951/425478951 UsedInRow(int (*) [25], int, int) [4]
259.56 0.00 590817023/590817023 UsedInCol(int (*) [25], int, int) [6]
90.96 0.00 1355081265/1355081265 UsedInBox(int (*) [25], int, int, int) [7]
-----------------------------------------------
1011.03 0.00 425478951/425478951 isSafe(int (*) [25], int, int, int) [3]
[4] 48.5 1011.03 0.00 425478951 UsedInRow(int (*) [25], int, int) [4]
-----------------------------------------------
525.53 0.00 876012758/876012758 SolveSudoku(int (*) [25]) [2]
[5] 25.2 525.53 0.00 876012758 FindUnassignedLocation(int (*) [25], int&, int&) [5]
-----------------------------------------------
259.56 0.00 590817023/590817023 isSafe(int (*) [25], int, int, int) [3]
[6] 12.4 259.56 0.00 590817023 UsedInCol(int (*) [25], int, int) [6]
-----------------------------------------------
90.96 0.00 1355081265/1355081265 isSafe(int (*) [25], int, int, int) [3]
[7] 4.4 90.96 0.00 1355081265 UsedInBox(int (*) [25], int, int, int) [7]
-----------------------------------------------
<spontaneous>
[8] 0.0 0.14 0.00 frame_dummy [8]
-----------------------------------------------
0.00 0.00 1/1 main [1]
[14] 0.0 0.00 0.00 1 printGrid(int (*) [25]) [14]
-----------------------------------------------
Index by function name
[2] SolveSudoku(int (*) [25]) [7] UsedInBox(int (*) [25], int, int, int) [14] printGrid(int (*) [25])
[5] FindUnassignedLocation(int (*) [25], int&, int&) [6] UsedInCol(int (*) [25], int, int) [8] frame_dummy
[3] isSafe(int (*) [25], int, int, int) [4] UsedInRow(int (*) [25], int, int)
Assignment 1: EasyBMP
EasyBMP Bitmap image library (Sample Program: Image to black and white renderer)
Library: http://easybmp.sourceforge.net/
| [Expand] Sample code: |
|---|
The program was compiled using the following commands:
g++ -c -pg -g BW.cpp EasyBMP.cpp g++ -pg BW.o EasyBMP.o -o BW rm *.o
Attempted to run the program with a number of files (8K resolution):
| [Expand] Sample Images |
|---|
| [Expand] Flat profile (Cabin): |
|---|
| [Expand] Flat profile (Lake): |
|---|
Assignment 1: Julia Sets
This portion of the assignment focuses on Julia sets with the quadratic formula:
fc(z) = z^2 + c; Where c and z are complex numbers
Psuedo code
for(Pixel pix in image){
pix.color = colorFunction(escapeValue(pix.loc, julia));
}
escapeValue(Complex loc, Complex julia){
int cycles = 0;
while(|loc| <=2 && ++cycles < MAXCYCLES){
loc = loc * loc + julia;
}
return cycles;
}
| [Expand] Julia.cpp |
|---|
To view the full c++ code github link
This code is tested using the parameters Range R(-1.5, 1.5) I(-1, 1) MAXCYCLES 1000 Julia values = .72 * e^(i*θ): θ[0, 2π] : 100 intervals
| [Expand] Flat Profiles |
|---|
| [Expand] Call Graphs |
|---|
| [Expand] Generated Image of Julia set at (-0.4, 0.6) |
|---|
This problem would be fairly simple to parallelize. In the image created by Julia sets each pixel is independent of the others. This problem involves Complex numbers, but that can be simply represented by using two arrays, or pairs of floats.
Assignment 1: Selection for parallelizing
After reviewing the three programs above, we decided to attempt to parallelize the Sudoku Solver Program for a few reasons.
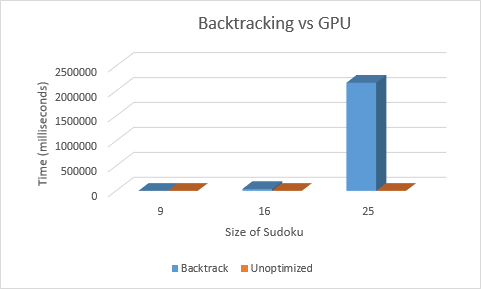
1. By increasing the dimensions of the smaller matrices that make up a sudoku by one, we see a major increase in the time it takes to solve the sudoku, from almost instantly to around 38 seconds, and then to 36 minutes. With a 25x25 sudoku (of 5x5 matrices), several functions were called over 100 million times.
2. Based on the massive time increases and similarity to the Hamiltonian Path Problem [2] which also uses backtracking to find a solution, we believe the run time of the sudoku solver to have a Big O notation that approaches O(n!) where 'n' is the number of blank spaces in the sudoku as the sudoku solver uses recursion to check every single possible solution, returning to previous steps if the tried solution does not work. O(n!) is an even worse runtime than O(n^2).
3. The Julia sets still took less than 6 minutes after increasing the image size, and the EasyBMP only took a few seconds to convert a large, high resolution image. Therefore, the Sudoku Solver had the greatest amount of time to be shaven off through optimization and thus offered the most challenge.
Assignment 2
| [Expand] Code for Solving a Sudoku using backtracking |
|---|
This code is capable of solving the 9x9 matrix supplied HOWEVER with the backtracking algorithm substituting values and the communications delay between the GPU and CPU, This code is unable to solve the 16x16 in any reasonable amount of time (I stopped it at 10+ minutes). If you consider the 130+ empty spaces in the grid I estimate over 130^2 calls to cudaMemcpy either way...
So we need an algorithm which will check each open spot, calculate all possible values which can fit there, and assign single values. We can also check each section (Box, row, col) for values which can only go in one place
| [Expand] Attempt One... |
|---|
Single Pass Sudoku Solver
This Kernel was designed to run on a single block with dimensions N*N the size of the Sudoku limiting us to a Sudoku of size 25 * 25 For each empty space, counts the number possible values which can fit and how many times each value can fit in that section If only one value can fit or that value has only one place, assigns the value
__global__ void superSolve(int * d_a) {
//Used to remember which row | col | box ( section ) have which values
__shared__ bool rowHas[N][N];
__shared__ bool colHas[N][N];
__shared__ bool boxHas[N][N];
//Used to ensure that the table has changed
__shared__ int added, past;
//Number of spaces which can place the number in each section
__shared__ int rowCount[N][N];
__shared__ int colCount[N][N];
__shared__ int boxCount[N][N];
//Where the square is located in the Sudoku
int row = threadIdx.x;
int col = threadIdx.y;
int box = row / BOXWIDTH + (col / BOXWIDTH) * BOXWIDTH;
//Unique identifier for each square in row, col, box
//Corresponds to the generic Sudoku Solve
//Using a Sudoku to solve a Sudoku !!!
int offset = col + (row % BOXWIDTH) * BOXWIDTH + (box % BOXWIDTH);
//Square's location in the Sudoku
int gridIdx = col * N + row;
int at = d_a[gridIdx];
if (!gridIdx) { //Thread at 0,0 sets values
added = -1;
past = -2;
}
rowHas[col][row] = false;
colHas[col][row] = false;
boxHas[col][row] = false;
__syncthreads();
if (at != UNASSIGNED) {
rowHas[row][at - 1] = true;
colHas[col][at - 1] = true;
boxHas[box][at - 1] = true;
}
//Previous loop has not changed any values
while (added != past) {
//RESET counters
rowCount[col][row] = 0;
colCount[col][row] = 0;
boxCount[col][row] = 0;
__syncthreads();
if (!gridIdx) //forget previous change
past = added;
int count = 0; //number of values which can fit in this square
int guess = at; //last value found which can fit in this square
for (int idx = 0; idx < N; ++idx) {
//Ensures that every square in each section is working on a different number in the section
int num = (idx + offset) % N;
if (at == UNASSIGNED && !(rowHas[row][num] || colHas[col][num] || boxHas[box][num])) {
count++;
guess = num + 1;
rowCount[row][num] ++;
colCount[col][num] ++;
boxCount[box][num] ++;
}
__syncthreads();
}
//Only ONE value can fit in this spot
if (count == 1) {
at = guess--;
d_a[gridIdx] = at;
rowHas[row][guess] = true;
colHas[col][guess] = true;
boxHas[box][guess] = true;
added = gridIdx;
}
__syncthreads();
if (at == UNASSIGNED) {
//Find values which can go in only one spot in the section
for (int idx = 0; idx < N; ++idx) {
if (!(rowHas[row][idx] || colHas[col][idx] || boxHas[box][idx]) &&
(boxCount[box][idx] == 1 || rowCount[row][idx] == 1 || colCount[col][idx] == 1)) {
//In this section this value can only appear in this square
at = idx + 1;
d_a[gridIdx] = at;
rowHas[row][idx] = true;
colHas[col][idx] = true;
boxHas[box][idx] = true;
added = gridIdx;
}
}
}
__syncthreads();
}
}
Assignment 3
Changes: Reduced Thread Divergence/CGMA -each thread now remembers which values it has seen in a boolean array - values are only assigned to the grid after the kernel 'solves' the sudoku - at value in kernel and shared memory for rowHas, colHas, boxHas, updated in a single place Coalesced Memory - change modifying _Has and _Count arrays from row->col to col->row as row(threadIdx.x) is our fastest moving dimension Clarified Code - use gridIdx == 0 rather then !gridIdx - use a do-while loop rather then a while loop
| [Expand] Full code |
|---|
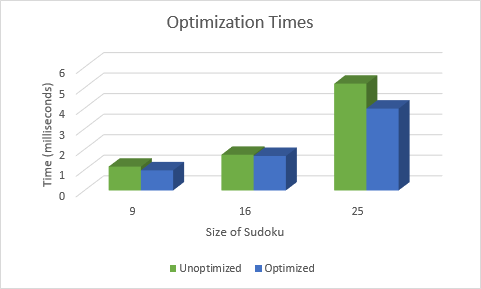
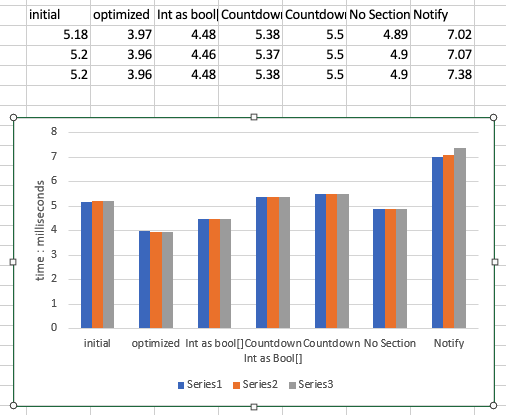
Kernel Optimization Attempts
These Kernels change a minor part of the Optimized Kernel or use a slightly different algorithm in an attempt to make it faster
Change : Replaces the boolean array hasSeen with a single int & uses bitwise operators
Theory : Since local array variables of threads are stored in Global memory this was an attempt to move that into a register
Result : No speed up noticed, suggesting that more is happening beyond arrays stored in Global memory, perhaps some type of paging,
more testing would be needed on something less erratic then a Sudoku Solver
| [Expand] Using a int as a boolean array |
|---|
Change : Remove the counters, and logic which checks for a section needing a value in one place
Theory : The counting logic requires a additional nested loop each solve cycle and created more thread divergence
Result : The algorithm is slower, probably because 'sections requiring a single value' adds more values early in the kernel resulting in less passes overall
Also this kernel is similar to one of my earlier builds, which was unable to solve the 9x9 getting stuck on every square having more then one possible value
| [Expand] Dropping Section Logic |
|---|
Change : Quickly finds one section that requires a single value in one spot, by checking all sections at once and remembering a single section Theory : Similar to the previous Kernel, trying to remove the second loop Result : Surprisingly slow, gains little benefit from the section logic and shared memory, yet is still required to count all values
| [Expand] Notify - Determines a single section that has a limited value (removes section loop) |
|---|
Change : Refactors the algorithm to count the total numbers that can fit in a square or section
Then counts down as values are added
Theory : Remove redundant counting logic that occurred during the Optimized Kernel each pass
Result : Not faster, HOWEVER there is a slight error, by setting notSeen = 0, the section counters will rarely reach one
| [Expand] CountDown - using Int as Boolean Array(EDITED now 4.28 seconds) |
|---|
Change : uses countdown logic with a boolean array Result : Similar times to other Countdown kernel
| [Expand] Countdown Boolean Array (EDITED - now 4.37ms) |
|---|
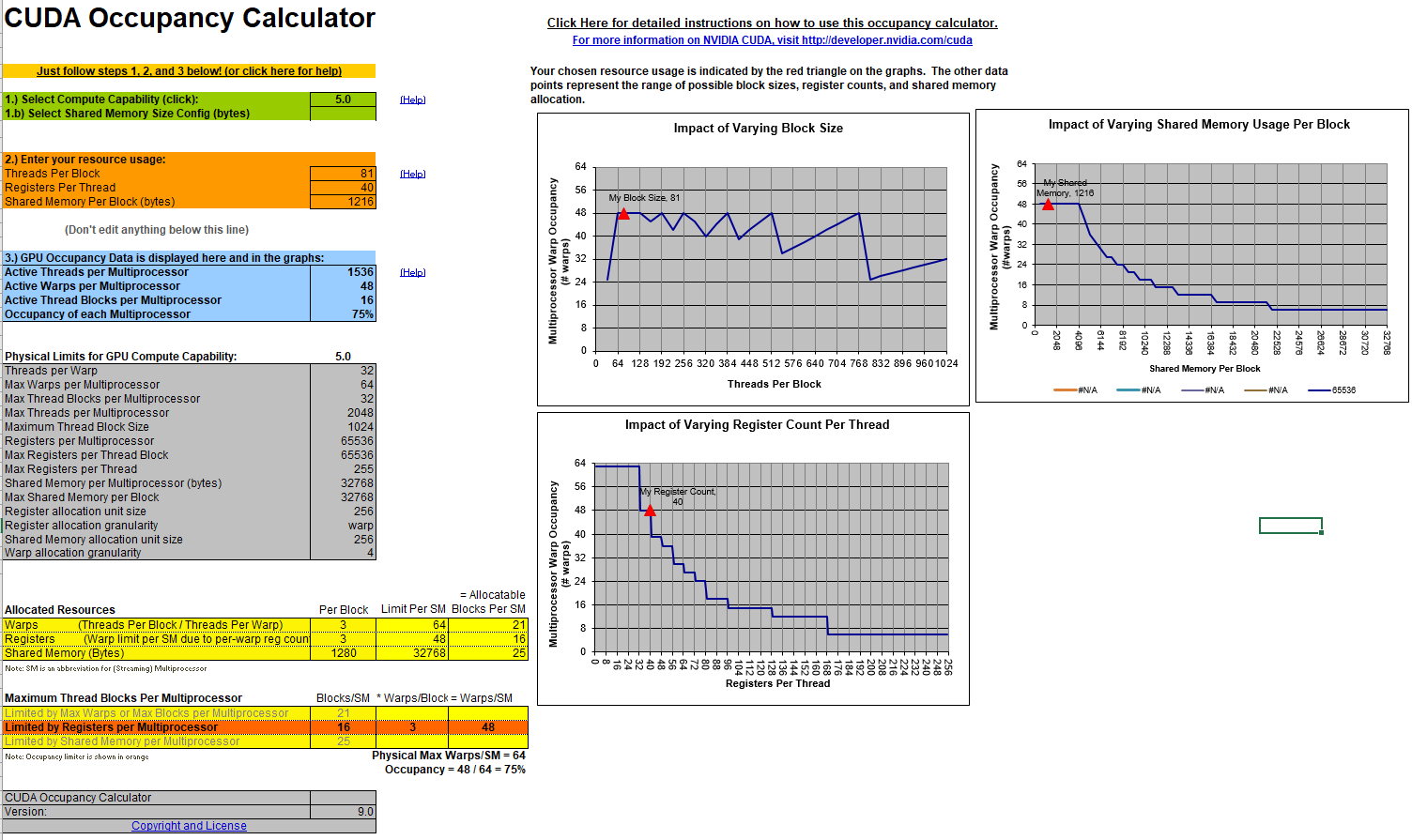
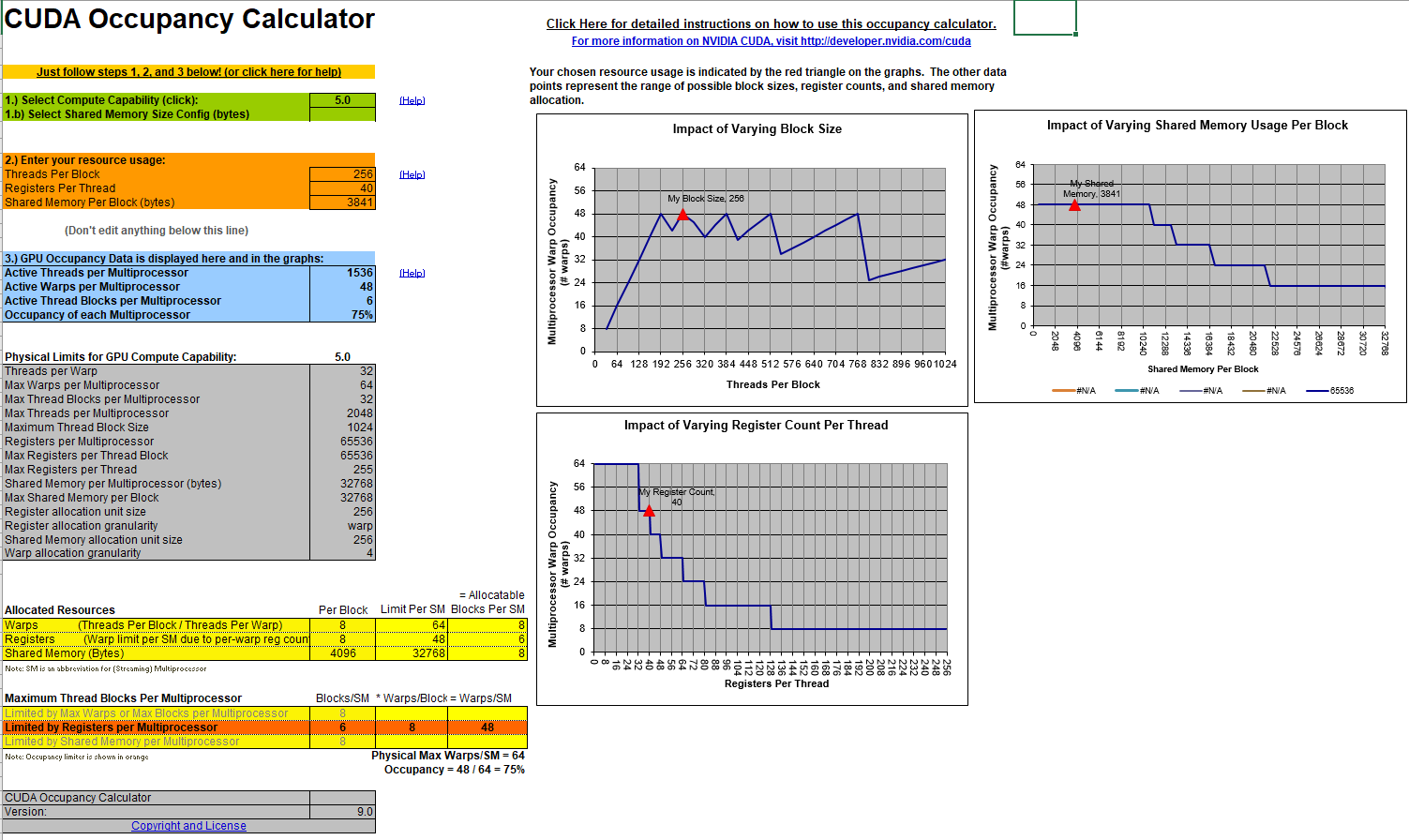
Occupancy Calculations
| [Expand] For 9x9: |
|---|
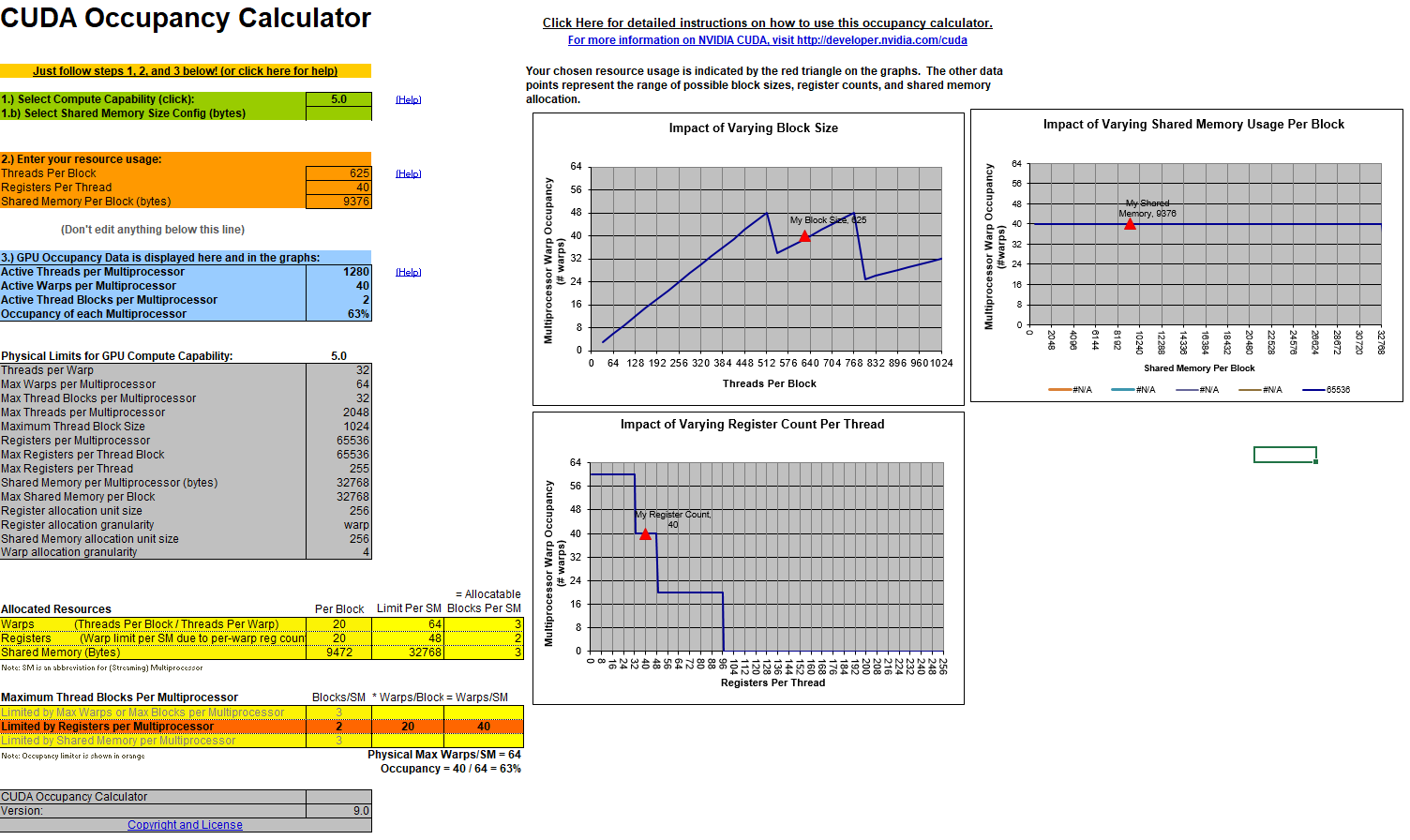
| [Expand] For 16x16: |
|---|
| [Expand] For 25x25: |
|---|