GPU621/Group 7
Contents
[hide]- 1 Intel Math Kernel Library
- 1.1 Overview
- 1.2 What is Math Kernel Library
- 1.3 Installation/Setup
- 1.4 Effectiveness of MKL in Matrix Multiplication
- 1.5 Matrix Multiplication Comparison Source Code
- 1.6 How MKL Improves Efficiency
- 1.7 Other Mathematical Functionality
- 1.8 Comparisons to AOCL and OpenBLAS
- 1.9 Advantages
- 1.10 Disadvantages
- 1.11 Conclusion
- 1.12 References
Intel Math Kernel Library
Overview
This project aims to explore the Intel Math Kernel Library and find out how it functions, its efficiency, as well as its advantages and disadvantages when utilized in the real world. This will be accomplished through an examination of how to include and apply Math Kernel Library functionality to a program, and the resulting effect on computational efficiency.
What is Math Kernel Library
Released on May 9, 2003, Intel's oneAPI Math Kernel Library, also known as Intel oneMKL or Intel MKL, is a library tailored towards the optimization of numerical computation in the fields such as science, engineering and finance. MKL functions by parallelizing computation routines processing on both the CPU and GPU. The library provides functionality improvements for calculations including:
- Linear algebra
- Fast Fourier transformations
- Vectorization and matrix operations
- Eigenvalue calculations
- Random number generation
MKL has seen use in the real world by handling data sets from a wide range of sources resulting in benefits such as assisting in applying machine learning techniques to large data sets and reducing the usage of energy in office buildings.
Installation/Setup
Follow the steps listed below in order to include Math Kernel Library functionality to a program. Alternatively Intel's MKL Get Started Guide can be referenced
In this case we will be using the online installer provided by Intel, support for offline installation and installation via packet managers is also available, for example NuGet Package Manager on Visual Studio.
1. Download MKL
2. Open installer
3. Follow installer instructions
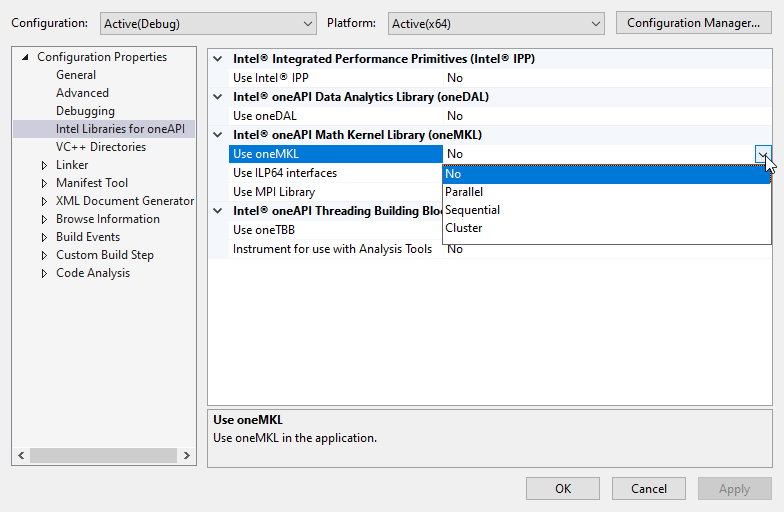
4. Access project properties in Visual Studio
5. Enable usage of MKL
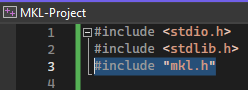
6. Include MKL header file "mkl.h"
Installing and compiling on Linux or macOS may require additional steps such as linking code.
Effectiveness of MKL in Matrix Multiplication
To determine the effectiveness of Math Kernel Library functionality, a comparison using matrix multiplication will be done to see the difference between unoptimized computation and computation using MKL. The source code for both sets of calculations are presented below.
Matrix Multiplication without MKL Optimization (nested loops)
printf (" Making the first run of matrix product using triple nested loop\n"
" to get stable run time measurements \n\n");
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
printf (" Measuring performance of matrix product using triple nested loop \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
}
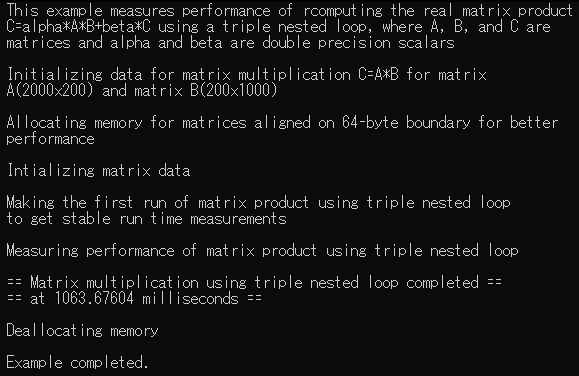
Result of Unoptimized Matrix Multiplication (using nested loops)
Matrix Multiplication with MKL Optimization (cblas_dgemm())
printf(" Making the first run of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface to get stable run time measurements \n\n");
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
printf(" Measuring performance of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
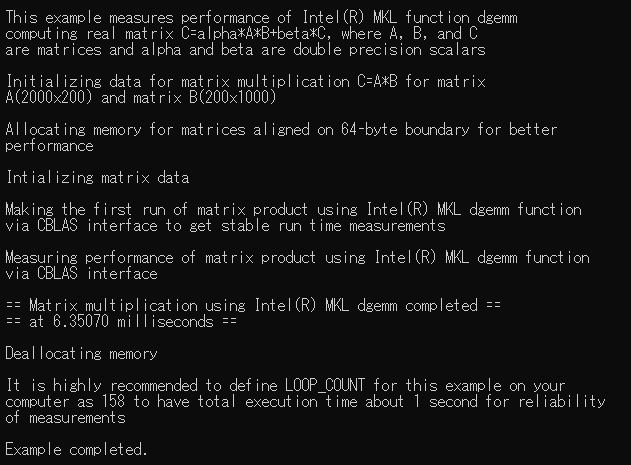
Result of Optimized Matrix Multiplication (using cblas_dgemm())
In this case, the effects of using MKL functionality can be clearly seen in a noticeable 167x increase in computation speed between the unoptimized and optimized calculations. While the proportional increase in performance may not always be so drastic, the difference in performance by using MKL extends both towards smaller and larger scales.
Matrix Multiplication Comparison Source Code
Full Source Code for Unoptimized Calculation
#define min(x,y) (((x) < (y)) ? (x) : (y))
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
/* Consider adjusting LOOP_COUNT based on the performance of your computer */
/* to make sure that total run time is at least 1 second */
#define LOOP_COUNT 10
int main()
{
double *A, *B, *C;
int m, n, p, i, j, k, r;
double alpha, beta;
double sum;
double s_initial, s_elapsed;
printf ("\n This example measures performance of rcomputing the real matrix product \n"
" C=alpha*A*B+beta*C using a triple nested loop, where A, B, and C are \n"
" matrices and alpha and beta are double precision scalars \n\n");
m = 2000, p = 200, n = 1000;
printf (" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf (" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double *)mkl_malloc( m*p*sizeof( double ), 64 );
B = (double *)mkl_malloc( p*n*sizeof( double ), 64 );
C = (double *)mkl_malloc( m*n*sizeof( double ), 64 );
if (A == NULL || B == NULL || C == NULL) {
printf( "\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf (" Intializing matrix data \n\n");
for (i = 0; i < (m*p); i++) {
A[i] = (double)(i+1);
}
for (i = 0; i < (p*n); i++) {
B[i] = (double)(-i-1);
}
for (i = 0; i < (m*n); i++) {
C[i] = 0.0;
}
printf (" Making the first run of matrix product using triple nested loop\n"
" to get stable run time measurements \n\n");
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
printf (" Measuring performance of matrix product using triple nested loop \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf (" == Matrix multiplication using triple nested loop completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
printf (" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
if (s_elapsed < 0.9/LOOP_COUNT) {
s_elapsed=1.0/LOOP_COUNT/s_elapsed;
i=(int)(s_elapsed*LOOP_COUNT)+1;
printf(" It is highly recommended to define LOOP_COUNT for this example on your \n"
" computer as %i to have total execution time about 1 second for reliability \n"
" of measurements\n\n", i);
}
printf (" Example completed. \n\n");
return 0;
}
Full Source Code for Optimized Calculations
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
/* Consider adjusting LOOP_COUNT based on the performance of your computer */
/* to make sure that total run time is at least 1 second */
#define LOOP_COUNT 10
int main()
{
double* A, * B, * C;
int m, n, p, i, r;
double alpha, beta;
double s_initial, s_elapsed;
printf("\n This example measures performance of Intel(R) MKL function dgemm \n"
" computing real matrix C=alpha*A*B+beta*C, where A, B, and C \n"
" are matrices and alpha and beta are double precision scalars\n\n");
m = 2000, p = 200, n = 1000;
printf(" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf(" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double*)mkl_malloc(m * p * sizeof(double), 64);
B = (double*)mkl_malloc(p * n * sizeof(double), 64);
C = (double*)mkl_malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) {
printf("\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf(" Intializing matrix data \n\n");
for (i = 0; i < (m * p); i++) {
A[i] = (double)(i + 1);
}
for (i = 0; i < (p * n); i++) {
B[i] = (double)(-i - 1);
}
for (i = 0; i < (m * n); i++) {
C[i] = 0.0;
}
printf(" Making the first run of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface to get stable run time measurements \n\n");
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
printf(" Measuring performance of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf(" == Matrix multiplication using Intel(R) MKL dgemm completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
printf(" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
if (s_elapsed < 0.9 / LOOP_COUNT) {
s_elapsed = 1.0 / LOOP_COUNT / s_elapsed;
i = (int)(s_elapsed * LOOP_COUNT) + 1;
printf(" It is highly recommended to define LOOP_COUNT for this example on your \n"
" computer as %i to have total execution time about 1 second for reliability \n"
" of measurements\n\n", i);
}
printf(" Example completed. \n\n");
return 0;
}
How MKL Improves Efficiency
In this instance the MKL used DGEMM to improve the calculation time. DGEMM stands for Double-precision, GEneral Matrix-Matrix multiplication. In the example used to demonstrate matrix multiplication, the code defines the multiplication of two matrices along with scaling factors alpha and beta. It can be noted that without MKL implementation the matrix multiplication is done though nested loops, however in the MKL optimized version cblas_dgemm() is called. The dgemm refers to DGEMM defined above and cblas refers to the CBLAS interface, which stands for Basic Linear Algebra Subprograms in C.
One part of BLAS, level 3, is dedicated to matrix-matrix operations, which in this case includes the matrix multiplication calculations. While the math and logic behind the implementation of the cblas_dgemm() function is fairly complicated, a simplified explanation on how it works can be expressed as the decomposition of either one or both of the matrices being multiplied and taking advantage of cache memory to improve computation speed. The decomposition of matrices into block matrices allows for general matrix-matrix multiplication to be conducted recursively. By using a beta parameter with the block matrices a multiplication calculation can be eliminated from each member of the resulting matrix
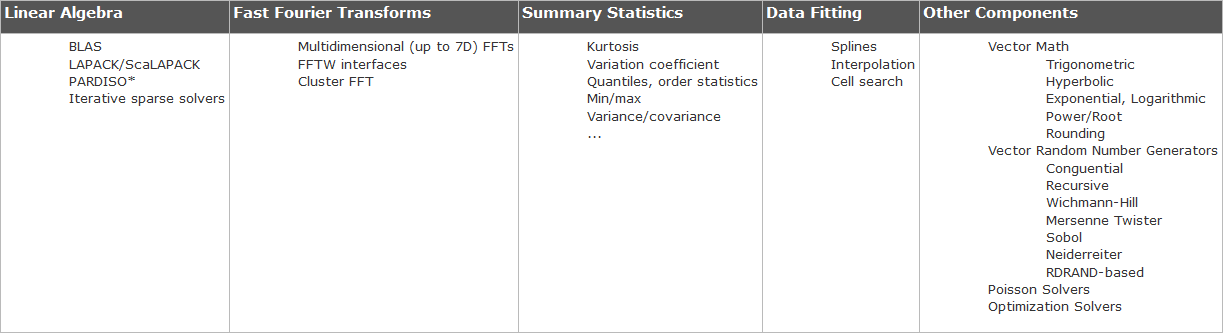
Other Mathematical Functionality
While the example used to explore the effectiveness of MKL utilizes matrix multiplication, the library provides functionality in a variety of other mathematical categories.
Some notable functionality provided in the Math Kernel Library include the following.
Basic Linear Algebra Subprograms (BLAS):
− level 1 BLAS: vector operations
− level 2 BLAS: matrix-vector operations
− level 3 BLAS: matrix-matrix operations
Sparse BLAS Level 1, 2, and 3: Basic operations on sparse vectors and matrices
LAPACK^2: Linear equations, least square problems, eigenvalues
ScaLAPACK^3: Computational, driver, and auxiliary routines for solving systems of linear equations across a compute cluster
PBLAS: Distributed vector, matrix-vector, and matrix-matrix operations
General and Cluster Fast Fourier Transform functions: Computation of Discrete Fourier Transformations and FFT across complete clusters
Solver Routines: Non linear least squares through Trust-Region algorithms
Data Fitting: Spline based approximation functions, derivatives, integrals and cell search
Additional examples of MKL functionality implemented in relation to real world models can be found in the optimization of various differential equations relating to finance. The Black-Scholes-Merton (BSM) model deals with pricing options contracts.
Serial
#include <omp.h>
#include <mathimf.h>
#include "euro_opt.h"
#ifdef __DO_FLOAT__
# define EXP(x) expf(x)
# define LOG(x) logf(x)
# define SQRT(x) sqrtf(x)
# define ERF(x) erff(x)
# define INVSQRT(x) 1.0f/sqrtf(x)
# define QUARTER 0.25f
# define HALF 0.5f
# define TWO 2.0f
#else
# define EXP(x) exp(x)
# define LOG(x) log(x)
# define SQRT(x) sqrt(x)
# define ERF(x) erf(x)
# define INVSQRT(x) 1.0/sqrt(x)
# define QUARTER 0.25
# define HALF 0.5
# define TWO 2.0
#endif
/*
// This function computes the Black-Scholes formula.
// Input parameters:
// nopt - length of arrays
// s0 - initial price
// x - strike price
// t - maturity
//
// Implementation assumes fixed constant parameters
// r - risk-neutral rate
// sig - volatility
//
// Output arrays for call and put prices:
// vcall, vput
//
// Note: the restrict keyword here tells the compiler
// that none of the arrays overlap in memory.
*/
void BlackScholesFormula_Compiler( int nopt,
tfloat r, tfloat sig, tfloat * restrict s0, tfloat * restrict x,
tfloat * restrict t, tfloat * restrict vcall, tfloat * restrict vput )
{
int i;
tfloat a, b, c, y, z, e;
tfloat d1, d2, w1, w2;
tfloat mr = -r;
tfloat sig_sig_two = sig * sig * TWO;
#pragma omp parallel for shared(s0, x, t, vcall, vput)
#pragma vector nontemporal (vcall, vput)
#pragma simd
for ( i = 0; i < nopt; i++ )
{
a = LOG( s0[i] / x[i] );
b = t[i] * mr;
z = t[i] * sig_sig_two;
c = QUARTER * z;
e = EXP ( b );
y = INVSQRT( z );
w1 = ( a - b + c ) * y;
w2 = ( a - b - c ) * y;
d1 = ERF( w1 );
d2 = ERF( w2 );
d1 = HALF + HALF*d1;
d2 = HALF + HALF*d2;
vcall[i] = s0[i]*d1 - x[i]*e*d2;
vput[i] = vcall[i] - s0[i] + x[i]*e;
}
}
MKL
#include <omp.h>
#include <mkl.h>
#include "euro_opt.h"
#ifdef __DO_FLOAT__
# define VDIV(n,a,b,r) vsDiv(n,a,b,r)
# define VLOG(n,a,r) vsLn(n,a,r)
# define VEXP(n,a,r) vsExp(n,a,r)
# define VINVSQRT(n,a,r) vsInvSqrt(n,a,r)
# define VERF(n,a,r) vsErf(n,a,r)
# define QUARTER 0.25f
# define HALF 0.5f
# define TWO 2.0f
#else
# define VDIV(n,a,b,r) vdDiv(n,a,b,r)
# define VLOG(n,a,r) vdLn(n,a,r)
# define VEXP(n,a,r) vdExp(n,a,r)
# define VINVSQRT(n,a,r) vdInvSqrt(n,a,r)
# define VERF(n,a,r) vdErf(n,a,r)
# define QUARTER 0.25
# define HALF 0.5
# define TWO 2.0
#endif
#if defined _VML_ACCURACY_EP_
# define VML_ACC VML_EP
#elif defined _VML_ACCURACY_LA_
# define VML_ACC VML_LA
#elif defined _VML_ACCURACY_HA_
# define VML_ACC VML_HA
#else
# error: _VML_ACCURACY_HA_/LA/EP should be defined in makefile
#endif
/* Set the reusable buffer for intermediate results */
#if !defined NBUF
# define NBUF 1024
#endif
/*
// This function computes the Black-Scholes formula.
// Input parameters:
// nopt - length of arrays
// s0 - initial price
// x - strike price
// t - maturity
//
// Implementation assumes fixed constant parameters
// r - risk-neutral rate
// sig - volatility
//
// Output arrays for call and put prices:
// vcall, vput
//
// Note: the restrict keyword here tells the compiler
// that none of the arrays overlap in memory.
//
// Note: the implementation assumes nopt is a multiple of NBUF
*/
void BlackScholesFormula_MKL( int nopt,
tfloat r, tfloat sig, tfloat * restrict s0, tfloat * restrict x,
tfloat * restrict t, tfloat * restrict vcall, tfloat * restrict vput )
{
int i;
tfloat mr = -r;
tfloat sig_sig_two = sig * sig * TWO;
#pragma omp parallel for \
shared(s0, x, t, vcall, vput, mr, sig_sig_two, nopt) \
default(none)
for ( i = 0; i < nopt; i+= NBUF )
{
int j;
tfloat *a, *b, *c, *y, *z, *e;
tfloat *d1, *d2, *w1, *w2;
__declspec(align(ALIGN_FACTOR)) tfloat Buffer[NBUF*4];
// This computes vector length for the last iteration of the loop
// in case nopt is not exact multiple of NBUF
#define MY_MIN(x, y) ((x) < (y)) ? (x) : (y)
int nbuf = MY_MIN(NBUF, nopt - i);
a = Buffer + NBUF*0; w1 = a; d1 = w1;
c = Buffer + NBUF*1; w2 = c; d2 = w2;
b = Buffer + NBUF*2; e = b;
z = Buffer + NBUF*3; y = z;
// Must set VML accuracy in each thread
vmlSetMode( VML_ACC );
VDIV(nbuf, s0 + i, x + i, a);
VLOG(nbuf, a, a);
#pragma simd
for ( j = 0; j < nbuf; j++ )
{
b[j] = t[i + j] * mr;
a[j] = a[j] - b[j];
z[j] = t[i + j] * sig_sig_two;
c[j] = QUARTER * z[j];
}
VINVSQRT(nbuf, z, y);
VEXP(nbuf, b, e);
#pragma simd
for ( j = 0; j < nbuf; j++ )
{
tfloat aj = a[j];
tfloat cj = c[j];
w1[j] = ( aj + cj ) * y[j];
w2[j] = ( aj - cj ) * y[j];
}
VERF(nbuf, w1, d1);
VERF(nbuf, w2, d2);
#pragma simd
for ( j = 0; j < nbuf; j++ )
{
d1[j] = HALF + HALF*d1[j];
d2[j] = HALF + HALF*d2[j];
vcall[i+j] = s0[i+j]*d1[j] - x[i+j]*e[j]*d2[j];
vput[i+j] = vcall[i+j] - s0[i+j] + x[i+j]*e[j];
}
}
}Comparisons to AOCL and OpenBLAS
Due to MKL being Intel's proprietary library the issue of performance arises when utilized on AMD platforms. It has been reported that MKL is slower on AMD hardware than Intel hardware, due to a check performed by MKL to determine if the processor used is Intel's or not. While this check can be circumvented, it is an extra step which may inconvenience those working on AMD systems.
AMD has its own set of libraries dealing with optimization, named AMD Optimizing CPU Libraries (AOCL). Instead of being based off of BLAS like MKL, AOCL is based off of BLIS, which stands for BLAS Like Interface Software. As can be seen from the name BLIS is functionally comparable to BLAS. The origin of BLIS dates back to the 2000s when BLAS needed to be updated due to improvements in computer architecture. BLIS focused on providing an alternative to BLAS, and as of modern times is capable of providing comparable performance to BLAS.
While Intel's MKL is regarded as one of the most efficient libraries dealing with mathematical computation, certain tests have shown AMD's AOCL can provide better performance in certain scenarios. A comparison done with Matrix-Matrix multiplication and Cholesky decomposition showed that AOCL could in some instances obtain a faster computation time than MKL. However it should be noted that there is variance between testing results based on hardware and deviation. The script used to perform the tests can be found below.
format compact
blas = version('-blas')
lapack = version('-lapack')
N=10000;
fprintf("Matrix size is %d x %d\n",N,N);
a = rand(N);
b = rand(N);
cholmat = a*a';
tic
c=a*b;
matmulTime = toc;
fprintf("Matrix Multiply time is %.2fs\n",matmulTime);
tic
c=a*b;
matmulTime = toc;
fprintf("Matrix Multiply time is %.2fs\n",matmulTime);
tic
c=a*b;
matmulTime = toc;
fprintf("Matrix Multiply time is %.2fs\n",matmulTime);
tic;
R = chol(cholmat);
cholTime = toc;
fprintf("Cholesky time is %.2fs\n",cholTime);
tic;
R = chol(cholmat);
cholTime = toc;
fprintf("Cholesky time is %.2fs\n",cholTime);
tic;
R = chol(cholmat);
cholTime = toc;
fprintf("Cholesky time is %.2fs\n",cholTime);
OpenBLAS is another open source implementation of the BLAS library dealing with mathematical computation. It was designed to be a successor to GotoBLAS and function on a wide variety of platforms such as x86, ARMv8, MIPS and RISC-V. OpenBLAS is much more portable and flexible in terms of utilization across systems than MKL, however it performs noticeably slower than MKL on a variety of tests, particularly for Eigenvalue computations.
| BLAS/LAPACK | Ordinarly Least Squares | Matrix Multiplication | Eigenvalue Computation |
|---|---|---|---|
| Built In | 2.294 | 100+ | 34.716 |
| OpenBLAS | 1.642 | 2.654 | 3.190 |
| MKL | 1.570 | 2.305 | 2.404 |
Again, it should be noted that if MKL were to be running on an AMD platform without bypassing the hardware check, it would perform slower than OpenBLAS. However, while the potential decrease in performance should be acknowledged, given the ability to circumvent it the maximum possible performance should be taken into consideration for the comparison instead.
Advantages
- Wide variety of functions
- Highly optimized computation algorithms
- Wide range of compatibility
- Effective use of parallelization in conjunction with hardware
Disadvantages
- Requires standalone installation and implementation
- Mathematical knowledge can be highly beneficial to efficient usage of library functionality
- Poor(er) compatibility and efficiency on AMD hardware
Conclusion
Intel Math Kernel Library is a powerful library which can greatly enhance a program's ability to perform mathematical computations. With proper knowledge on how to effectively utilize MKL functionality, the overall efficiency of the program can be drastically improved. Usage of MKL has already yielded real world results in a variety of fields, and will continue to do so as the scope of programs, data and the issues they tackle increases.
References
https://www.sciencedirect.com/topics/computer-science/intel-math-kernel-library
https://iq.opengenus.org/blas-vs-blis/
https://scrp.econ.cuhk.edu.hk/blog/analysis/2022/02/07/mkl-optimization.html