GPU621/Intel oneMKL - Math Kernel Library
Contents
- 1 Intel® oneAPI Math Kernel Library
- 1.1 Group Members
- 1.2 Introduction
- 1.3 Progress Report
- 1.4 Main Fountain
- 1.5 Setting up MKL
- 1.6 MKL Testing
- 1.7 Output
- 1.8 Source Code
- 1.9 Intel®-Optimized Math Library for Numerical Computing
- 1.10 References
Intel® oneAPI Math Kernel Library
Group Members
- Menglin Wu
- Syed Muhammad Saad Bukhari
- Lin Xu
Introduction
Intel Math Kernel Library, or now known as oneMKL (as part of Intel’s oneAPI), is a library of highly optimized and extensively parallelized routines, that was built to provide maximum performance across a variety of CPUs and accelerators.
There are many functions included in domains such as sparse and dense linear algebra, sparse solvers, fast Fourier transforms, random number generation, basic statistics etc., and there are many routines supported by the DPC++ Interface on CPU and GPU.
Progress Report
progress 100%
Main Fountain
Solve large-scale calculation problems, provide BLAS, LAPACK linear algebra programs, fast Fourier transform, vector mathematical functions, random number generation functions, and other functions.
1) BLAS and LAPACK
Deploying highly optimized basic linear algebra routines BLAS (Basic Linear Algebra Subroutines) and linear algebra package LAPACK (Linear Algebra Package) routines in Intel processors provides significant performance improvements.
2) ScaLAPACK
ScaLAPACK is a parallel computing software package suitable for MIMD parallel machines with distributed storage. ScaLAPACK provides several linear algebra solving functions, which are highly efficient, portable, scalable, and highly reliable. Using its solving library, parallel applications based on linear algebra operations can be developed.
The Intel® MKL implementation of ScaLAPACK can provide significant performance improvements far beyond what a standard NETLIB implementation can achieve.
3) PARDISO sparse matrix solver
Use the PARDISO direct sparse matrix solver to solve large sparse linear equations. The solver is authorized by the University of Basel. It is an easy-to-use, thread-safe, high-performance memory-efficient software library. Intel? MKL also includes a conjugate gradient solver and FGMRES iterative sparse matrix solver.
4) Fast Fourier Transform (FFT)
Take advantage of multi-dimensional FFT subroutines (from 1 to 7 dimensions) with a new, easy-to-use C/Fortran interface. Intel? MKL supports distributed memory clusters that use the same API, allowing workloads to be easily distributed to a large number of processors, thereby achieving substantial performance improvements. In addition, Intel? MKL also provides a series of C language routines ("wrapper"), these routines can simulate FFTW 2.x and 3.0 interfaces, thereby supporting current FFTW users to integrate Intel? MKL into existing applications.
5) Vector Math Library (VML)
The Vector Math Library uses vector implementations of computationally intensive core mathematical functions (power functions, trigonometric functions, exponential functions, hyperbolic functions, logarithmic functions, etc.) to significantly increase the application speed.
6) Vector Statistics Library-Random Number Generator (VSL)
Use the Vector Statistical Library (Vector Statistical Library) random number generator to accelerate the simulation, so as to achieve a system performance improvement far higher than that of the scalar random number generator.
Setting up MKL
First, you need to download the mkl library from the intel official website through the URL: https://www.intel.com/content/www/us/en/developer/tools/oneapi/base-toolkit-download.html
Then you need to set additional include directories and additional library directories on visual studio, don’t forget to change the configuration and platform.
Thirdly, set use intel mkl to sequential in the Intel Math Kernel Library.
Finally, modify the additional dependencies with the help of the URL https://www.intel.com/content/www/us/en/developer/tools/oneapi/onemkl-link-line-advisor.html
MKL Testing
In this project I want to compare the running time of the serial version and the optimized version of MKL under multithreading.
The dgemm routine can perform several calculations, so here is two same soulutions to calculate.
C = alpha *A * B + beta * C
Integers indicating the size of the matrices:
A: m rows by k columns
B: k rows by n columns
C: m rows by n columns
alpha
Real value used to scale the product of matrices A and B.
A
Array used to store matrix A.
k
Leading dimension of array A, or the number of elements between successive rows (for row major storage) in memory. In the case of this exercise the leading dimension is the same as the number of columns.
B
Array used to store matrix B.
beta
Real value used to scale matrix C.
C
Array used to store matrix C.
n
Leading dimension of array C, or the number of elements between successive rows (for row major storage) in memory. In the case of this exercise the leading dimension is the same as the number of columns.
serial version
clock_t startTime = clock();
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p * i + k] * B[n * k + j];
C[n * i + j] = sum;
}
}
clock_t endTime = clock();
MKL version
Used to set the number of threads that MKL runs, mkl_set_num_threads().
max_threads = mkl_get_max_threads();
printf(" Finding max number %d of threads Intel(R) MKL can use for parallel runs \n\n", max_threads);
printf(" Running Intel(R) MKL from 1 to %i threads \n\n", max_threads * 2);
for (i = 1; i <= max_threads * 2; i++) {
for (j = 0; j < (m * n); j++)
C[j] = 0.0;
mkl_set_num_threads(i);
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
Output
| serial | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
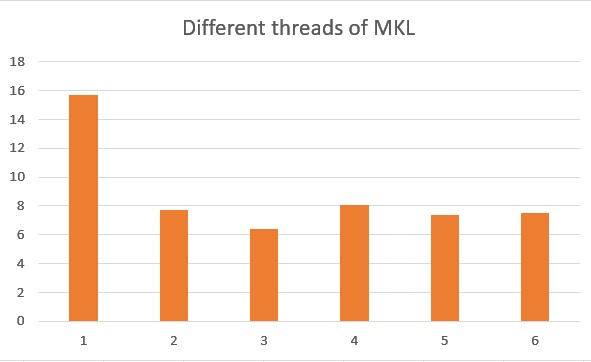
| 9000 | 15.7 | 7.7 | 6.4 | 8.1 | 7.4 | 7.5 |
Here is my computer's number of logical processors.
wmic:root\cli>cpu get numberoflogicalprocessors NumberOfLogicalProcessors 6
When mkl_get_max_threads is equal to the number of physical cores, the performance is the best, not the number of threads, which is the following 3 instead of 6.
Through matrix calculation (BLAS), Intel mkl can significantly improve performance and is optimized for multi-threading.
Source Code
Serial
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
/* Consider adjusting LOOP_COUNT based on the performance of your computer */
/* to make sure that total run time is at least 1 second */
#define LOOP_COUNT 220 //220 for more accurate statistics
int main()
{
double* A, * B, * C;
int m, n, p, i, j, k, r;
double alpha, beta;
double sum;
double s_initial, s_elapsed;
printf("\n This example demonstrates threading impact on computing real matrix product \n"
" C=alpha*A*B+beta*C using Intel(R) MKL function dgemm, where A, B, and C are \n"
" matrices and alpha and beta are double precision scalars \n\n");
m = 2000, p = 200, n = 1000;
printf(" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf(" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double*)malloc(m * p * sizeof(double), 64);
B = (double*)malloc(p * n * sizeof(double), 64);
C = (double*)malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) {
printf("\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
free(A);
free(B);
free(C);
return 1;
}
printf(" Intializing matrix data \n\n");
for (i = 0; i < (m * p); i++) {
A[i] = (double)(i + 1);
}
for (i = 0; i < (p * n); i++) {
B[i] = (double)(-i - 1);
}
for (i = 0; i < (m * n); i++) {
C[i] = 0.0;
}
clock_t startTime = clock();
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p * i + k] * B[n * k + j];
C[n * i + j] = sum;
}
}
clock_t endTime = clock();
s_elapsed = (endTime - startTime) / LOOP_COUNT;
printf(" == Matrix multiplication using triple nested loop completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
printf(" Deallocating memory \n\n");
free(A);
free(B);
free(C);
if (s_elapsed < 0.9 / LOOP_COUNT) {
s_elapsed = 1.0 / LOOP_COUNT / s_elapsed;
i = (int)(s_elapsed * LOOP_COUNT) + 1;
printf(" It is highly recommended to define LOOP_COUNT for this example on your \n"
" computer as %i to have total execution time about 1 second for reliability \n"
" of measurements\n\n", i);
}
printf(" Example completed. \n\n");
return 0;
}
MKL version
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
/* Consider adjusting LOOP_COUNT based on the performance of your computer */
/* to make sure that total run time is at least 1 second */
#define LOOP_COUNT 220 // 220 for more accurate statistics
int main()
{
double* A, * B, * C;
int m, n, p, i, j, r, max_threads;
double alpha, beta;
double s_initial, s_elapsed;
printf("\n This example demonstrates threading impact on computing real matrix product \n"
" C=alpha*A*B+beta*C using Intel(R) MKL function dgemm, where A, B, and C are \n"
" matrices and alpha and beta are double precision scalars \n\n");
m = 2000, p = 200, n = 1000;
printf(" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf(" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double*)mkl_malloc(m * p * sizeof(double), 64);
B = (double*)mkl_malloc(p * n * sizeof(double), 64);
C = (double*)mkl_malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) {
printf("\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf(" Intializing matrix data \n\n");
for (i = 0; i < (m * p); i++) {
A[i] = (double)(i + 1);
}
for (i = 0; i < (p * n); i++) {
B[i] = (double)(-i - 1);
}
for (i = 0; i < (m * n); i++) {
C[i] = 0.0;
}
max_threads = mkl_get_max_threads();
printf(" Finding max number %d of threads Intel(R) MKL can use for parallel runs \n\n", max_threads);
printf(" Running Intel(R) MKL from 1 to %i threads \n\n", max_threads * 2);
for (i = 1; i <= max_threads * 2; i++) {
for (j = 0; j < (m * n); j++)
C[j] = 0.0;
mkl_set_num_threads(i);
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf(" == Matrix multiplication using Intel(R) MKL dgemm completed ==\n"
" == at %.5f milliseconds using %d thread(s) ==\n\n", (s_elapsed * 1000), i);
}
printf(" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
if (s_elapsed < 0.9 / LOOP_COUNT) {
s_elapsed = 1.0 / LOOP_COUNT / s_elapsed;
i = (int)(s_elapsed * LOOP_COUNT) + 1;
printf(" It is highly recommended to define LOOP_COUNT for this example on your \n"
" computer as %i to have total execution time about 1 second for reliability \n"
" of measurements\n\n", i);
}
printf(" Example completed. \n\n");
return 0;
}
Intel®-Optimized Math Library for Numerical Computing
Data Parallel C++ (DPC++) APIs, with OpenMP acceleration, maximizes performance and portability across architectures in science, engineering, and finance using enhanced math routines
Data Parallel C++
DPC++ is an open alternative to single-architecture proprietary languages.
Foundations
OneAPI concepts are demonstrated in the Vector Add sample as well as using the DPC++ programming language.
- Device selectors targeting different accelerators including GPU and FPGA
- Buffers and accessors
- Queues
- Data parallel kernel “parallel_for”
A Code Walk-Through for DPC++ Foundations
OneAPI concepts and functionality are demonstrated in this sample walk-through through vector_add, which is written in Data Parallel C++. The program adds two arrays of integers together using hardware acceleration.
- DPC++ headers
- Asynchronous exceptions from kernels
- Device selectors for different accelerators
- Buffers and accessors
- Queues
- parallel_for kernel
DPC++Headers
DPC++ is based on familiar and industry-standard C++, plus it incorporates the SYCL* specification 1.2.1 from the Khronos Group* and includes language extensions developed using an open community process. The header file sycl.hpp, as specified in the SYCL specification, is also provided in the Intel® oneAPI DPC++/C++ Compiler. FPGA support is included with a DPC++ extension with the fpga_extensions.hpp header file. The code below, from vector_add,illustrates the different headers needed when you are supporting different accelerators.
DPC++ Kernels Exceptions
DPC++ kernels run asynchronously on accelerators in different stackframes. The kernel may have asynchronous errors that cannot be propagated up to the stack. In order to catch the asynchronous exceptions, the SYCL queue class incorporates error handler functions.
Selector for Accelerators
SYCL and oneAPI selectors can discover and provide access to the hardware available on host environment. The default_selector selects the most performant accelerator, while DPC++ provides additional selector classes for the FPGA accelerator.
Queue and parallel_for Kernels
A DPC++ queue encapsulates the context required by kernel execution. A queue can take a specific device selector and an asynchronous exception handler, as is used in vector_add. Three different types of kernels: single task kernel, basic data-parallel kernel, hierarchical parallel kernel, are used in kernel execution, while the basic data-parallel, parallel_for kernel, is used in vector_add. The kernel body is an addition of two arrays captured in the Lambda function. sum[i] = a[i] + b[i];
- The range of data the kernel can process is specified in the first parameter num_items of h.parallel_for. Example: A 1-D range with size of num_items. Two read-only data, a_array and b_array, are transferred to the accelerator by the runtime. When the kernel is completed, the sum of the data in the sum_buf buffer is copied to host when the sum_buf goes out of scope.
oneAPI programs are built on device selectors, buffers, accessors, queues and kernels. DPC++ incorporates SYCL and community extensions to simplify data parallel programming. DPC++ allows code reuse across hardware targets, and enables high productivity and performance across CPU, GPU, and FPGA architectures, while permitting accelerator-specific tuning.
The Mandelbrot Set is a program that demonstrates oneAPI concepts and functionally using the DPC++ programming language.
- Unified shared memory
- Managing and accessing memory
- Parallel implementation
The host offers three distinct allocation types of memory, host memory, device memory and shared memory managed by compiler. Unified Shared Memory, USM, is an alternative to buffers for managing and accessing memory from the host and device. The program calculates if each point in a two-dimensional complex plane exists in the set, using parallel computing patterns and DPC++. The code walkthrough uses a Mandelbrot sample to explore USM. This walkthrough demonstrates how you can use familiar C/C++ patterns to manage data within host and device memory, using Mandlebrot as a test case.
Driver Functions: main.cpp
The driver function, main.cpp, contains the infrastructure to execute and evaluate the computation of the Mandelbrot set.
Queue Creation
The queue is created in main using the default selector, which first attempts to launch a kernel code on the GPU, and then it falls back to the Host/CPU if no compatible device is found. It utilizes the dpc_common exception handler, which allows for asynchronous exception handling of your kernel code.
ShowDevice()
The ShowDevice() function displays information about the chosen device.
Execute()
The Execute() function initializes the MandelParallelUsm object, uses it to evaluate the Mandelbrot set, and outputs the results.
Mandelbrot USM Usage
MandleParameter Class
The MandelParameter struct contains all the necessary functionality to calculate the Mandelbrot set.
Datatype: ComplexF
The MandelParameter defines a datatype ComplexF,which represents a complex floating-point number. typedef std::complex<float> ComplexF;
Point()
The Point() function takes a complex point,c, as an argument and determines whether or not it belongs to the Mandelbrot set. The function checks for how many iterations (up to an arbitrary max_iterations) that the parameter, z, remains bounded given the recursive function, zn+1 = (zn)2 + c, where z0= 0. Then it returns the number of iterations.
ScaleRow()/ScaleCol()
The scale functions convert row/column indices to coordinates within the complex plane. This is necessary to convert array indices to their corresponding complex coordinates. This application can be seen below in the MandelParallelUsm Class section.
Mandle Class
MandelParallelUsm inherits from its parent class, the Mandel class. It contains member functions for outputting the data visualization, addressed in the Other Functions section below. Member Variables
- MandelParameters p_: A MandelParameters object
- int *data_: A pointer to the memory for storing the output data
MandleParallelUsm Class
This class is derived from the Mandel class, and handles all the device code for offloading the Mandelbrot calculation using USM.
Device Initialization: Constructor
The MandelParallelUSM constructor first calls the Mandel constructor, which assigns the values of the arguments to their corresponding member variables. It passes the address of the queue object to the member variable, q, so that it can later be used to launch the device code. Finally, it calls the Alloc() virtual member function.
USM Initialization: Alloc()
The Alloc() virtual member function is overridden in the MandelParallelUsm class to enable USM. It calls malloc_shared() which creates and returns the address to a block of memory. This is shared across the host and device.
Launching the Kernel: Evaluate()
The Evaluate() member function launches the kernel code and calculates the Mandelbrot set. Inside parallel_for(), the work item id (index) is mapped to row and column coordinates, which are used to construct a point in the complex plane using the ScaleRow()/ScaleCol() functions. The MandelParameters Point() function is called to determine if the complex point belongs to the Mandelbrot set, with its result written to the corresponding location in shared memory.
The destructor frees the shared memory by calling the Free() member function, ensuring no memory leaks in the program.
Other Functions
Producing a Basic Visualization of the Mandlebrot Set
The Mandel class also contains member functions for data visualization. WriteImage() generates a PNG image representation of the data, where each pixel represents a point on the complex plane, and its luminosity represents the iteration depth calculated by Point().
Example Image of Data Output
The Mandel class’s Print()member function produces a similar visualization as is written to stdout.
References
https://www.intel.com/content/www/us/en/developer/tools/oneapi/onemkl.html#gs.hfplbb