Group 6

From CDOT Wiki
Revision as of 22:15, 7 April 2019 by Yyuan34 (talk | contribs) (→‎The Monte Carlo Simulation (PI Calculation))
Jump to: navigation, search


GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary

Group 6

Team Members

  1. Xiaowei Huang
  2. Yihang Yuan
  3. Zhijian Zhou

Email All

Progress

Assignment 1 - Select and Assess

Array Processing

Subject: Array Processing

Blaise Barney introduced Parallel Computing https://computing.llnl.gov/tutorials/parallel_comp/ Array processing could become one of the parallel example, which "demonstrates calculations on 2-dimensional array elements; a function is evaluated on each array element."

Here is my source code

[Expand] arrayProcessing.cpp 
 
// arrayProcessing.cpp
// Array processing implement parallel solution 
#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <ctime>

void init(float** randomValue, int n) {
	//std::srand(std::time(nullptr));
    float f = 1.0f / RAND_MAX;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			randomValue[i][j] = std::rand() * f;
}

void multiply(float** a, float** b, float** c, int n) {
    for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++) {
            float sum = 0.0f;
            for (int k = 0; k < n; k++)
				sum += a[i][k] * b[k][j];
            
			c[i][j] = sum;
			if(n <= 10){
				std::cout << "array c[" << i << "," << j << "]: " << c[i][j] << std::endl;
			}
        }
}

int main(int argc, char* argv[]) {
    // interpret command-line argument
    if (argc != 2) {
        std::cerr << argv[0] << ": invalid number of arguments\n"; 
        std::cerr << "Usage: " << argv[0] << "  size_of_matrices\n"; 
		return 1;
    }
    int n  = std::atoi(argv[1]);   // size of matrices

    float** a = new float*[n];
    for (int i = 0; i < n; i++)       
		a[i] = new float[n];
    float** b = new float*[n];
    for (int i = 0; i < n; i++)
        b[i] = new float[n];
    float** c = new float*[n];
    for (int i = 0; i < n; i++)
        c[i] = new float[n];
    
	std::srand(std::time(nullptr));
    init(a, n);
    init(b, n);

    multiply(a, b, c, n);

    for (int i = 0; i < n; i++)
        delete [] a[i];
    delete [] a;
    for (int i = 0; i < n; i++)
        delete [] b[i];
    delete [] b;
    for (int i = 0; i < n; i++)
		delete [] c[i];
    delete [] c;
}


Standard random method is used to initialize a 2-dimentional array. The purpose of this program is to perform a 2-dimension array calculation, which is a matrix-matrix multiplication in this example.

In this following profile example, n = 1000 

Flat profile:
Each sample counts as 0.01 seconds.
  %   cumulative   self              self     total           
 time   seconds   seconds    calls  Ts/call  Ts/call  name    
100.11      1.48     1.48                             multiply(float**, float**, float**, int)
  0.68      1.49     0.01                             init(float**, int)
  0.00      1.49     0.00        1     0.00     0.00  _GLOBAL__sub_I__Z4initPPfi

Call graph

granularity: each sample hit covers 2 byte(s) for 0.67% of 1.49 seconds

index % time    self  children    called     name
                                             <spontaneous>
[1]     99.3    1.48    0.00                 multiply(float**, float**, float**, int) [1]
-----------------------------------------------
                                             <spontaneous>
[2]      0.7    0.01    0.00                 init(float**, int) [2]
-----------------------------------------------
                0.00    0.00       1/1       __libc_csu_init [16]
[10]     0.0    0.00    0.00       1         _GLOBAL__sub_I__Z4initPPfi [10]
-----------------------------------------------
�
Index by function name
  [10] _GLOBAL__sub_I__Z4initPPfi (arrayProcessing.cpp) [2] init(float**, int) [1] multiply(float**, float**, float**, int)

From the call graph, multiply() took major runtime to more than 99%, as it contains 3 for-loop, which T(n) is O(n^3). Besides, init() also became the second busy one, which has a O(n^2).

As the calculation of elements is independent of one another - leads to an embarrassingly parallel solution. Arrays elements are evenly distributed so that each process owns a portion of the array (subarray). It can be solved in less time with multiple compute resources than with a single compute resource.

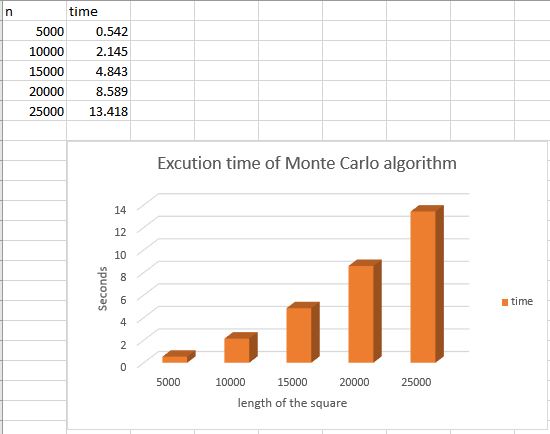
The Monte Carlo Simulation (PI Calculation)

Subject: The Monte Carlo Simulation (PI Calculation) Got the code from here: https://rosettacode.org/wiki/Monte_Carlo_methods#C.2B.2B A Monte Carlo Simulation is a way of approximating the value of a function where calculating the actual value is difficult or impossible.

It uses random sampling to define constraints on the value and then makes a sort of "best guess."


[Expand] Source Code 
#include<iostream>
#include<fstream>
#include<math.h>
#include<stdlib.h>
#include<time.h>

using namespace std;

void calculatePI(int n, float* h_a) {
	float x, y;
	int hit;
	srand(time(NULL));
	for (int j = 0; j < n; j++) {
		hit = 0;
		x = 0;
		y = 0;
		for (int i = 0; i < n; i++) {
			x = float(rand()) / float(RAND_MAX);
			y = float(rand()) / float(RAND_MAX);
			if (y <= sqrt(1 - (x * x))) {
				hit += 1;
			}
		}
		h_a[j] = 4 * float(hit) / float(n);
	}
}

int main(int argc, char* argv[]) {

	if (argc != 2) {
		std::cerr << argv[0] << ": invalid number of arguments\n";
		std::cerr << "Usage: " << argv[0] << "  size_of_matrices\n";
		return 1;
	}
	int n = std::atoi(argv[1]); // scale
	float* cpu_a;
	cpu_a = new float[n];


	calculatePI(n, cpu_a);

	ofstream h_file;
	h_file.open("h_result.txt");
	float cpuSum = 0.0f;
	for (int i = 0; i < n; i++) {
		cpuSum += cpu_a[i];
		h_file << "Host: " << cpu_a[i] << endl;
	}
	cpuSum = cpuSum / (float)n;
	cout << "CPU Result: " << cpuSum << endl;
	h_file.close();
}

Yihang.JPG

Zhijian

Subject:


Assignment 2 - Parallelize

Serial Code: 

void calculatePI(int n, float* h_a) {
	float x, y;
	int hit;
	srand(time(NULL));
	for (int j = 0; j < n; j++) {
		hit = 0;
		x = 0; 
		y = 0;
		for (int i = 0; i < n; i++) {
			x = float(rand()) / float(RAND_MAX);
			y = float(rand()) / float(RAND_MAX);
			if (y <= sqrt(1 - (x * x))) {
				hit += 1;
			}
		}

		h_a[j] = 4 * float(hit) / float(n);

	}
}

Parallel code: 

__global__ void setRng(curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	curand_init(123456, idx, 0, &rng[idx]);
}


__global__ void calPI(float* d_a, int n, curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;

	unsigned int counter = 0;
	while (counter < n) {
		float x = curand_uniform(&rng[idx]);
		float y = curand_uniform(&rng[idx]);

		if (y <= sqrt(1 - (x * x))) {
			d_a[idx]++;
		}
		counter++;
	}
	d_a[idx] = 4.0 * (float(d_a[idx])) / float(n);
}

Assignment 3 - Optimize

Here is my final source code

[Expand] p03_reduction.cu 
 
// part 3.1 : reduction
// update 2: 
// add comments to all kernels
// mdf kernel 2 only returns the numbers of dot inside the quadrant, and this number passes to next blocks
// new kernel 3 sums the elements of d_a as generated by the kernel 2, and accumulate the block sums
// new kernel 4 sums all block PI value before passing back to host

#include<iostream>
#include<fstream>
#include<math.h>
#include<stdlib.h>
#include<time.h>
#include <chrono>
#include <cstdlib>
#include <iomanip>

#include <cuda_runtime.h>
#include <curand_kernel.h>
// to remove intellisense highlighting
#include <device_launch_parameters.h>
#ifndef __CUDACC__
#define __CUDACC__
#endif
#include <device_functions.h>

using namespace std;
using namespace std::chrono;
const int ntpb = 512;

// this function uses to calculate PI on CPU 
void calculatePI(int n, float* h_a) {
	float x, y;
	int hit;
	srand(time(NULL));
	for (int j = 0; j < n; j++) {
		hit = 0;
		x = 0;
		y = 0;
		for (int i = 0; i < n; i++) {
			x = float(rand()) / float(RAND_MAX);
			y = float(rand()) / float(RAND_MAX);
			if (y <= sqrt(1 - (x * x))) {
				hit += 1;
			}
		}

		h_a[j] = 4 * float(hit) / float(n);

	}
}


// kernel 1
// The first kernel uses to generate random numbers 
__global__ void setRng(curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	curand_init(123456, idx, 0, &rng[idx]);
}

// kernel 2
// The second kernel identifis the dot location (use the kernel 1 passed random number to create) 
// whether it is been in the quadrant or not 
__global__ void calPI(float* d_a, int n, curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	unsigned int counter = 0;		// this variable counts the total number of dot be placed
	unsigned int hit = 0;			// this variable counts the number of dot inside the cirle
	
	// in one Threat, it generates n dots
	while (counter < n) {
		float x = curand_uniform(&rng[idx]);
		float y = curand_uniform(&rng[idx]);

		if (y*y <= (1 - (x * x))) {
			hit++;
		}
		counter++;
	}

	d_a[idx] = 4.0 * (float(hit)) / float(n);
}

// kernel 3 
// the third kernel sum the result in each block 
__global__ void sumPi(float* d_a, float*d_b, const int n) {		 
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	int t = threadIdx.x;
	__shared__ float s[ntpb];
	s[t] = d_a[i];
	__syncthreads();

	// sum the data in shared memory 
	for (int stride = 1; stride < blockDim.x; stride <<= 1) {
		if ((t % (2 * stride) == 0) && (i + stride <  n)) {
			s[t] += s[t + stride];
		}
		__syncthreads();
	}

	// store the sum in d_b; 
	if (t == 0) {
		d_b[blockIdx.x] = s[0];
	}
}

// kernel 4
// the forth kernel sum the result of all blocks
__global__ void accumulate(float* c, const int nblocks) {
	// store the elements of c[] in shared memory
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	int t = threadIdx.x;
	__shared__ float s[ntpb];
	s[t] = c[i];
	__syncthreads();

	// sum the data in shared memory
	for (int stride = 1; stride < blockDim.x; stride <<= 1) {
		if ((t % (2 * stride) == 0) && (i + stride <  nblocks)) {
			s[t] += s[t + stride];
		}
		__syncthreads();
	}

	// store the sum in c[0]
	if (t == 0) {
		c[blockIdx.x] = s[0];
	}
}

void reportTime(const char* msg, steady_clock::duration span) {
	auto ms = duration_cast<milliseconds>(span);
	std::cout << msg << " took - " <<
		ms.count() << " millisecs" << std::endl;
}

int main(int argc, char* argv[]) {

	if (argc != 2) {
		std::cerr << argv[0] << ": invalid number of arguments\n";
		std::cerr << "Usage: " << argv[0] << "  size_of_matrices\n";
		return 1;
	}
	int n = std::atoi(argv[1]); // scale
	int nblks = (n + ntpb - 1) / ntpb;

	cout << "scale: " << n << endl << endl;
	steady_clock::time_point ts, te;

	float* cpu_a;
	cpu_a = new float[n];

	ts = steady_clock::now();
	calculatePI(n, cpu_a);
	te = steady_clock::now();
	reportTime("CPU", te - ts);


	ofstream h_file;
	h_file.open("h_result.txt");
	float cpuSum = 0.0f;
	for (int i = 0; i < n; i++) {
		cpuSum += cpu_a[i];
		h_file << "Host: " << cpu_a[i] << endl;
	}
	cpuSum = cpuSum / (float)n;
	cout << "CPU Result: " << cpuSum << endl;
	h_file.close();

	cout << endl;
	////////////////////////////////////////

	curandState *d_rng;
	float* d_a;
	float* d_b;
	float* h_a;
	h_a = new float[n];

	cudaMalloc((void**)&d_a, n * sizeof(float));
	cudaMalloc((void**)&d_b, n * sizeof(float));
	cudaMalloc((void**)&d_rng, n * sizeof(curandState));

	ts = steady_clock::now();

	setRng << < nblks, ntpb >> > (d_rng);
	cudaDeviceSynchronize();

	// calculate PI in each thread and pass its value
	calPI << <nblks, ntpb >> > (d_a, n, d_rng);
	cudaDeviceSynchronize();

	// sum PI in total and pass back on the device
	sumPi << <nblks, ntpb >> > (d_a, d_b, n);	
	cudaDeviceSynchronize();

	// accumulate the block sums 
	accumulate << <1, nblks >> >(d_b, nblks);
	cudaDeviceSynchronize();

	te = steady_clock::now();
	reportTime("GPU", te - ts);

	// host h_a only receives one element from device d_b
	cudaMemcpy(h_a, d_b, n * sizeof(float), cudaMemcpyDeviceToHost);


	ofstream d_file;
	d_file.open("d_result.txt");
	float gpuSum = 0.0f;
	gpuSum = h_a[0] / (float)n;
	cout << "GPU Result: " << gpuSum << "\n \n"<< endl;
	d_file.close();

	cudaFree(d_a);
	cudaFree(d_rng);
	delete[] cpu_a;
	delete[] h_a;

	// reset the device
	cudaDeviceReset();
}
Retrieved from "https://wiki.cdot.senecapolytechnic.ca/w/index.php?title=Group_6&oldid=138893"