GPU610/TeamKappa
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
Team Kappa
Team Members
- Ryan Mullings, Team Member
- Andy Cooc, Team Member
- Matt Jang, Team Member
Assignment 1
Program 1: RSA Encryption
Code From Github: link
Profiling
- gprof: Encryption 10MB
% cumulative self self total time seconds seconds calls s/call s/call name 60.48 1.50 1.50 3495254 0.00 0.00 fastModularExp(unsigned long long, unsigned long long, unsigned long long) 32.66 2.31 0.81 3495254 0.00 0.00 findHighestSetBit(unsigned long long) 4.44 2.42 0.11 1 0.11 2.48 encryption(std::string, std::string, std::string) 2.42 2.48 0.06 3495254 0.00 0.00 intToByteArray(int, char*) 0.00 2.48 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10encryptionSsSsSs 0.00 2.48 0.00 1 0.00 0.00 _GLOBAL__sub_I_main 0.00 2.48 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 2.48 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
- gprof: Encryption 20MB
% cumulative self self total time seconds seconds calls s/call s/call name 63.65 3.27 3.27 6990507 0.00 0.00 fastModularExp(unsigned long long, unsigned long long, unsigned long long) 29.04 4.75 1.49 6990507 0.00 0.00 findHighestSetBit(unsigned long long) 3.90 4.96 0.20 1 0.20 5.13 encryption(std::string, std::string, std::string) 3.41 5.13 0.17 6990507 0.00 0.00 intToByteArray(int, char*) 0.00 5.13 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10encryptionSsSsSs 0.00 5.13 0.00 1 0.00 0.00 _GLOBAL__sub_I_main 0.00 5.13 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 5.13 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
- gprof: Encryption 30MB
% cumulative self self total time seconds seconds calls s/call s/call name 68.04 5.11 5.11 10485760 0.00 0.00 fastModularExp(unsigned long long, unsigned long long, unsigned long long) 25.23 7.00 1.90 10485760 0.00 0.00 findHighestSetBit(unsigned long long) 3.99 7.30 0.30 1 0.30 7.51 encryption(std::string, std::string, std::string) 2.73 7.51 0.20 10485760 0.00 0.00 intToByteArray(int, char*) 0.00 7.51 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10encryptionSsSsSs 0.00 7.51 0.00 1 0.00 0.00 _GLOBAL__sub_I_main 0.00 7.51 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 7.51 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
- gprof: Decryption 10MB
% cumulative self self total time seconds seconds calls s/call s/call name 69.80 1.71 1.71 3495254 0.00 0.00 fastModularExp(unsigned long long, unsigned long long, unsigned long long) 21.63 2.24 0.53 3495254 0.00 0.00 findHighestSetBit(unsigned long long) 6.12 2.39 0.15 1 0.15 2.45 decryption(std::string, std::string, std::string) 2.45 2.45 0.06 3495254 0.00 0.00 intToByteArray(int, char*) 0.00 2.45 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10encryptionSsSsSs 0.00 2.45 0.00 1 0.00 0.00 _GLOBAL__sub_I_main 0.00 2.45 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 2.45 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
- gprof: Decryption 20MB
% cumulative self self total time seconds seconds calls s/call s/call name 64.11 3.38 3.38 6990507 0.00 0.00 fastModularExp(unsigned long long, unsigned long long, unsigned long long) 27.18 4.82 1.44 6990507 0.00 0.00 findHighestSetBit(unsigned long long) 4.73 5.07 0.25 1 0.25 5.28 decryption(std::string, std::string, std::string) 3.98 5.28 0.21 6990507 0.00 0.00 intToByteArray(int, char*) 0.00 5.28 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10encryptionSsSsSs 0.00 5.28 0.00 1 0.00 0.00 _GLOBAL__sub_I_main 0.00 5.28 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 5.28 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
- gprof: Decryption 30MB
% cumulative self self total time seconds seconds calls s/call s/call name 66.88 5.25 5.25 10485760 0.00 0.00 fastModularExp(unsigned long long, unsigned long long, unsigned long long) 24.59 7.18 1.93 10485760 0.00 0.00 findHighestSetBit(unsigned long long) 5.73 7.63 0.45 1 0.45 7.85 decryption(std::string, std::string, std::string) 2.80 7.85 0.22 10485760 0.00 0.00 intToByteArray(int, char*) 0.00 7.85 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10encryptionSsSsSs 0.00 7.85 0.00 1 0.00 0.00 _GLOBAL__sub_I_main 0.00 7.85 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 7.85 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
Bottleneck Code
The two slowest parts of this encryption method are fastModularExp and findHighestSetBit. A third function, intToByteArray, takes up a relatively small amount of time but may still be able to be optimized.
unsigned int fastModularExp(ULong a, ULong b, ULong c) {
ULong result = 1;
ULong leadingbit = findHighestSetBit(b); // Heighest set bit
while(leadingbit > 0){ //while there are bits left
result = ((result*result) % c); //case 1: bit is a 0
if((b & leadingbit) > 0){
result = ((result * a) % c); //case 2: if bit is a 1
}
leadingbit = leadingbit >> 1;
}
return (unsigned int)result;
}
ULong findHighestSetBit(ULong num){
ULong result = 0;
for(int i = 63; i >= 0; i--){
if(num & (1ULL << i)){
result = 1ULL << i;
return result;
}
}
return result;
}
byte* intToByteArray(int num, byte *result){
for(int i = 0; i < 4; i++){
result[i] = (num & (0xFF << (8 *(3-i)))) >> (8 *(3-i));
}
return result;
}
At first glance, the fastest function is also the function that appears like it would be the easiest to run on a GPU. The other code does not look like it can be optimized with a GPU easily as it does not use large arrays of N size. However, after some short internet research, several documents turned up on the topic of using a GPU to make RSA faster (example: here and here). This leaves me hopeful that in the further stages of this assignment that this could be an interesting program to work with.
Ryan Mullings: Program 2-Image Manipulation Processor
I decided to profile an Image manipulation program since it had many different functions that I could play around with. Also depending on the number of files you enter as arguments the processor will display different options Source Code:link to dream in code
Sample Run
Code for some of the manipulations
Profiles
- Profile for shrinking image by 2
% cumulative self total time seconds calls s/call s/call name 40.22 5.75 2 0.00 0.00 Image(Image const&) 27.53 3.32 1 0.00 0.00 readImage(char*, Image&) 13.23 2.21 1 0.00 2.48 shrinkImage(int, Image&) 12.67 2.11 1 0.00 0.00 Image(int, int, int) 6.32 2.48 1 0.00 0.00 writeImage(char*, Image&)
- Profile for Expanding image by 3 and Rotating by 20 degrees
% cumulative self total time seconds calls s/call s/call name 64.28 11.23 1 0.00 0.00 rotateImage(Image const&) 16.89 4.51 1 0.00 0.00 enlargeImage(char*, Image&) 13.23 2.21 1 0.00 0.00 writeImage(int, Image&)
Essentially, all of the functions are the main hotspots from the test runs.
Program 3: Serial pi Calculation - C version
I've decided to profile the calculate (estimate) of pi using a "dartboard" algorithm.
The program is described as the follows:
* FILE: ser_pi_calc.c * DESCRIPTION: * Serial pi Calculation - C Version * This program calculates pi using a "dartboard" algorithm. See * Fox et al.(1988) Solving Problems on Concurrent Processors, vol.1 * page 207. * AUTHOR: unknown * REVISED: 02/23/12 Blaise Barney * Throw darts at board. Done by generating random numbers * between 0 and 1 and converting them to values for x and y * coordinates and then testing to see if they "land" in * the circle." If so, score is incremented. After throwing the * specified number of darts, pi is calculated. The computed value * of pi is returned as the value of this function, dboard.
Source file
Hardware and software
Operating System: Windows 7 Ultimate 64-bit (6.1, Build 7601) Service Pack 1 (7601.win7sp1_gdr.151019-1254)
Processor: Intel(R) Core(TM) i7-3740QM CPU @ 2.70GHz (8 CPUs), ~2.7GHz
Available OS Memory: 16280MB RAM
Graphics: NVIDIA GeForce GT 650M
Software: Visual Studio 2013 Ultimate
CUDA 7.5
Profiling
By default the argument 100000 darts and 100 rounds.
using matrix@seneca I entered the following commands.
compiled using
g++ -O2 -g -pg -opi ser_pi_calc.c
execute
pi
gprof:
gprof -p -b bs > result.flt
view result
cat result.flt
results:
Float profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 100.00 0.03 0.03 dboard(int)
It appears it only calls the dboard(int) function
Code Snippet
for (n = 1; n <= darts; n++) {
/* generate random numbers for x and y coordinates */
r = (double)random()/cconst;
x_coord = (2.0 * r) - 1.0;
r = (double)random()/cconst;
y_coord = (2.0 * r) - 1.0;
/* if dart lands in circle, increment score */
if ((sqr(x_coord) + sqr(y_coord)) <= 1.0)
score++;
}
/* calculate pi */
pi = 4.0 * (double)score/(double)darts;
return(pi);
}
Plans
Using the serial Pi calculator/estimator, benchmark a large amount of sampling which reaches the limit of my computer. Perhaps changing the number of round to one and and run the maximum sampling size and accuracy that my computer can handle.
Problem
When using the code with visual studio, I had errors trying to compile it. It appears after some time searching online, the #include <time.h> function void srandom(unsigned seed); and random() does not come standard in all ANSI code so I tried the approach using srand(time(NULL)) and rand(); and still failed resulting returns of 0.0000. zeroes. I modified the code for the random generate number and added report time and pretty much kept the idea the same into a simpler program.
Code
#include <iostream>
#include <ctime>
#include <cstdlib>
#include <chrono>
using namespace std::chrono;
double generateNumber() {
const double randf = 1.0f / (double)RAND_MAX;
return std::rand() * randf;
}
void reportTime(const char* msg, steady_clock::duration span) {
double nsecs = double(span.count()) *
steady_clock::period::num / steady_clock::period::den;
std::cout << msg << " - took - " <<
nsecs << " secs" << std::endl;
}
// report system time
/* void reportTime(const char* msg, steady_clock::duration span) {
auto ms = duration_cast<milliseconds>(span);
std::cout << msg << " - took - " <<
ms.count() << " millisecs" << std::endl;
}
*/
int main(int argc, char* argv[])
{
double dart = std::atoi(argv[1]);
steady_clock::time_point ts, te;
double x, y;
int i;
int score = 0;
double z;
double pi;
ts = steady_clock::now();
for (i = 0; i<dart; ++i) {
x = (double)generateNumber();
y = (double)generateNumber();
z = sqrt((x*x) + (y*y));
if (z <= 1)
++score;
}
pi = ((double)score / (double)dart)*4.0;
std::cout << "After " << i << " throws, average pi is " << pi << std::endl;
te = steady_clock::now();
reportTime("pi calculation", te - ts);
}
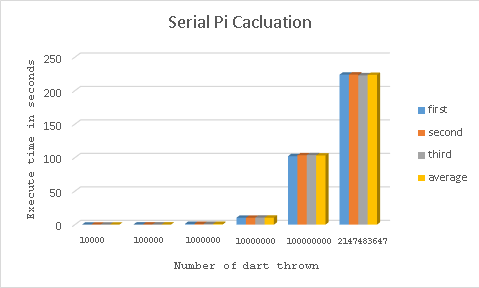
Results, bottlenecks, and benchmark
It appears my computer's limitation is 2147483647 samples
After 2147483647 throws, average pi is 3.14152
pi calculation - took - 223.884 secs
| n | first | second | third | average |
|---|---|---|---|---|
| 10000 | 0.0156s | 0.0156s | 0s | 0.0104s |
| 100000 | 0.1092s | 0.1092s | 0.1092s | 0.1092s |
| 1000000 | 1.0452s | 1.0296s | 1.0452s | 1.04s |
| 10000000 | 10.299s | 10.2542s | 10.4092s | 10.3208s |
| 100000000 | 102.19s | 103.553s | 103.728s | 103.157s |
| 2147483647 | 223.884s | 223.996s | 222.882s | 223.5873s |
Summary
The Big-O Classification for serial pi calculator (estimate) appears to be O(1) run time.
Part 2 of Pi
Interesting enough, I had stumbled upon a monte carlo pi calculation written with "Parallel.For" to speed up the sampling using multi-threads (concurrency) on the CPU. I figured I'll compare my results to this with the serial program I was working on. Since this part is part of the parallelization of the program, I will be posting in the part 2 of the assignment.
Source File
the source code can be found at github
Code Snippet
int main()
{
srand(time(NULL));
const int N1 = 1000;
const int N2 = 100000;
int n = 0;
int c = 0;
Concurrency::critical_section cs;
// it is better that N1 >> N2 for better performance
Concurrency::parallel_for(0, N1, [&](int i)
{
int t = monte_carlo_count_pi(N2);
cs.lock(); // race condition
n += N2; // total sampling points
c += t; // points fall in the circle
cs.unlock();
});
cout << "pi ~= " << setprecision(9) << (double)c / n * 4.0 << endl;
return 0;
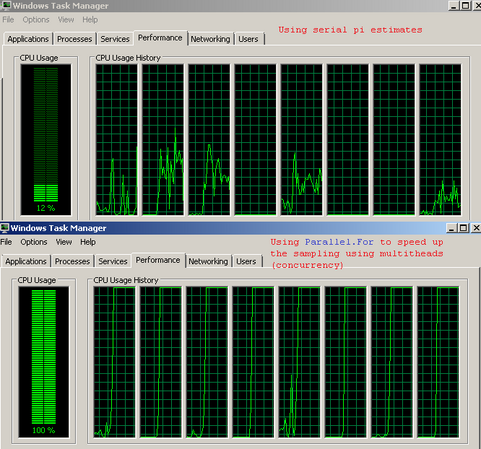
}When comparing the serial version and the parallel.for version of pi's usage of the CPU resource. You can see the CPU concurrency version demonstrates the benefit of multi-core processors.
kernel CUDA version work in progress...and comparasions
Code Snippet of kernel
__global__ void montecarlo(const double* d_x, const double* d_y, int* d_score) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
if ((d_x[idx]) * (d_x[idx]) +
(d_y[idx]) * (d_y[idx]) <= 1){
d_score[idx] = 1;
}
else
d_score[idx] = 0;
}
</code>
Assignment 2
For assignment 2, we have elected to parallelize the image manipulation program that Ryan Mullings looked at for the first assignment. This program preforms algorithms on black and white *.pgm image files.
Image Manipulation: Rotation
For all benchmarks, the image was rotated 45 degrees counter clockwise. The following is the example input and output from running one of the tests:
C:\Users\Matt\Documents\Visual Studio 2013\Projects\A2\rotate>GPU 1600_900.pgm 1600_900_gpu.pgm
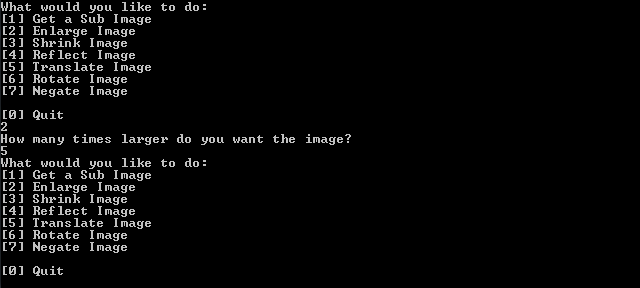
What would you like to do:
[1] Get a Sub Image
[2] Enlarge Image
[3] Shrink Image
[4] Reflect Image
[5] Translate Image
[6] Rotate Image
[7] Negate Image
[0] Quit
6
Enter to what degree you want to rotate the image:
45
method: rotate - cuda (122)
method: rotate - full (168)
What would you like to do:
[1] Get a Sub Image
[2] Enlarge Image
[3] Shrink Image
[4] Reflect Image
[5] Translate Image
[6] Rotate Image
[7] Negate Image
[0] Quit
0
You have chosen to close the progam.
Press any key to continue . . .
All benchmarks were run with the following system specs:
- AMD FX-8150 Eight-Core 3.6 GHz
- Cuda 7.5
- NVIDIA GeForce GTX 670
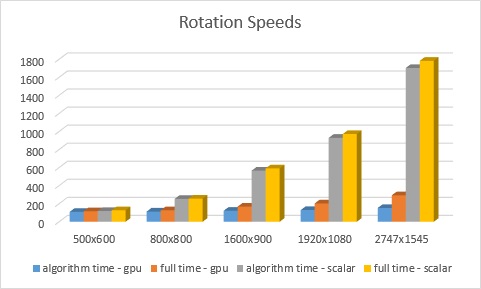
Benchmark
image size
algorithm time - gpu
full time - gpu
algorithm time - scalar
full time - scalar
500 x 600
109ms
117ms
119ms
127ms
800 x 800
113ms
127ms
254ms
256ms
1600 x 900
122ms
168ms
567ms
592ms
1920 x 1080
130ms
203ms
930ms
972ms
2747 x 1545
153ms
293ms
1704ms
1783ms
Scalar Code
void Image::rotateImage(int theta, Image& source) {
steady_clock::time_point first_start;
first_start = steady_clock::now();
int rows = source.N;
int cols = source.M;
Image temp(rows, cols, source.Q);
steady_clock::time_point second_start;
second_start = steady_clock::now();
float rads = (theta * 3.14159265) / 180.0;
for (int r = 0; r < rows; r++) {
for (int c = 0; c < cols; c++) {
int new_row = (int)(rows / 2 + ((r - rows / 2) * cos(rads)) - ((c - cols / 2) * sin(rads)));
int new_col = (int)(cols / 2 + ((r - rows / 2) * sin(rads)) + ((c - cols / 2) * cos(rads)));
if (inBounds(new_row, new_col)) {
temp.pixelVal[new_row][new_col] = source.pixelVal[r][c];
}
}
}
profile("rotate - cuda", steady_clock::now() - second_start);
for (int r = 0; r < rows; r++) {
for (int c = 0; c < cols; c++) {
if (temp.pixelVal[r][c] == 0) {
temp.pixelVal[r][c] = temp.pixelVal[r][c + 1];
}
}
}
source = temp;
profile("rotate - full", steady_clock::now() - first_start);
}
GPU Code
const unsigned ntpb = 1024;
__global__ void kernel_rotate(int * old_image, int * temp_image, float rads, int rows, int cols) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index > rows * cols) {
return;
}
int row = index % rows;
int col = index / rows;
int new_row = (int)(rows / 2 + ((row - rows / 2) * cos(rads)) - ((col - cols / 2) * sin(rads)));
int new_col = (int)(cols / 2 + ((row - rows / 2) * sin(rads)) + ((col - cols / 2) * cos(rads)));
if (!(new_row >= rows || new_row < 0 || new_col >= cols || new_col < 0)) {
temp_image[rows * new_col + new_row] = old_image[index];
}
}
void Image::rotateImage(int theta, Image & source) {
steady_clock::time_point first_start;
first_start = steady_clock::now();
int rows = source.N;
int cols = source.M;
int nb = (rows * cols + ntpb - 1) / ntpb;
int * d_temp_image;
int * d_old_image;
int * h_temp_image = new int[rows * cols];
int * h_old_image = new int[rows * cols];
for (int r = 0; r < rows; r++) {
for (int c = 0; c < cols; c++) {
h_old_image[rows * c + r] = source.pixelVal[r][c];
}
}
steady_clock::time_point second_start;
second_start = steady_clock::now();
cudaMalloc((void**)&d_old_image, rows * cols * sizeof(int));
if (!d_old_image) {
cout << "CUDA: out of memory (d_old_image)" << endl;
return;
}
cudaMalloc((void**)&d_temp_image, rows * cols * sizeof(int));
if (!d_temp_image) {
cout << "CUDA: out of memory (d_temp_image)" << endl;
return;
}
cudaMemcpy(d_old_image, h_old_image, rows * cols * sizeof(int), cudaMemcpyHostToDevice);
dim3 dGrid(nb);
dim3 dBlock(ntpb);
kernel_rotate <<<dGrid, dBlock>>>(d_old_image, d_temp_image, (theta * 3.14159265) / 180.0, rows, cols);
cudaDeviceSynchronize();
cudaMemcpy(h_temp_image, d_temp_image, rows * cols * sizeof(int), cudaMemcpyDeviceToHost);
profile("rotate - cuda", steady_clock::now() - second_start);
for (int r = 0; r < rows; r++) {
for (int c = 0; c < cols; c++) {
if (h_temp_image[rows * c + r] == 0 && c + 1 < cols)
source.pixelVal[r][c] = h_temp_image[rows * (c + 1) + r];
else
source.pixelVal[r][c] = h_temp_image[rows * c + r];
}
}
profile("rotate - full", steady_clock::now() - first_start);
}
Summary
For the rotation code, at around 500x600 dimensions or 300,000 pixels, the speed is about the same. However, as the image size increases, the scalar code will become much slower in comparison to the GPU code. To parallelize the code, I just used the straight forward tactic of unrolling the two for loops and assigning one thread for what would be each iteration. Since each index of the array was looked at individually, there is no problem doing that. As you can see in the benchmarks, through this process the speed was reduced greatly at higher resolutions.
Assignment 3 (Matt Jang)
Image Rotation
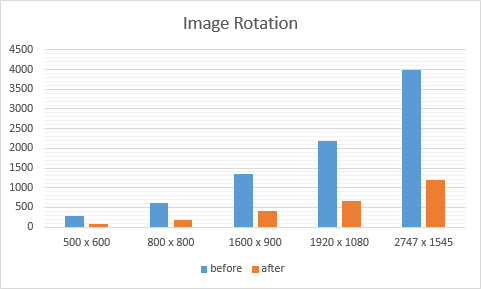
This is the kernel that I had originally made for Assignment 2. To optimize this I wanted to make use of all the techniques that we learned in class like shared memory and the like. Although I wasn't able to take advantage of everything I wanted to do, I was still able to speed up this kernel to preform between 3 and 4 times faster. The following are the steps that I used to optimize.
- Changed the number of threads per block to 128 from 1024.
- This step was to improve the occupancy. However, the occupancy was already high on my card so this didn't make much of a difference. On the smallest image, the time went from 293μs to 265μs and on the largest image, the time went from 3995μs to 3617μs.
- Optimized out rows/2 and cols/2 into parameters.
- Since this operation was preformed every single iteration, I figured it would be quicker to pass through that value in the parameters. On the smallest image, the time went from 265μs to 193μs and on the largest image, the time went from 3617μs to 2621μs.
- Used device functions __cosf and __sinf.
- In class we had learned that there were special device functions for trigonometry. I figured I would use them but the speed up was much more than I had expected. On the smallest image, the time went from 193μs to 93μs and on the largest image, the time went from 2621μs to 1232μs.
- Optimize uses of __cosf and __sinf.
- Since using the device functions made such a big change and since there were two identical calls to each, I stored the value of their result in a register and used the register twice. This didn't make such a big change but I am sure that if I had done it before using __cosf and __sinf, the difference would have been much bigger. On the smallest image, the tiem went from 93μs to 91μs and on the largest image, the time went from 1232μs to 1196μs.
- Experimental division optimization.
- This last optimization made almost no difference but I more wanted to try something new. I changed "int col = index / rows;" to "int col = (index - row) / rows;". The idea is that if the computer gets a whole number from division, it would be a bit faster. I don't fully understand why it worked but there was a consistent speed up of around 0.5% to 1%. On the smallest image, the time went from 91μs to 90μs and on the largest image, the time went from 1196μs to 1191μs.
Kernel Speeds
Image Size
Before
After
500 x 600
293μs
90μs
800 x 800
613μs
188μs
1600 x 900
1359μs
408μs
1920 x 1080
2175μs
654μs
2747 x 1545
3995μs
1191μs
Unoptimized
const unsigned ntpb = 1024;
__global__ void kernel_rotate(int * old_image, int * temp_image, float rads, int rows, int cols) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index > rows * cols) {
return;
}
int row = index % rows;
int col = index / rows;
int new_row = (int)(rows / 2 + ((row - rows / 2) * cos(rads)) - ((col - cols / 2) * sin(rads)));
int new_col = (int)(cols / 2 + ((row - rows / 2) * sin(rads)) + ((col - cols / 2) * cos(rads)));
if (!(new_row >= rows || new_row < 0 || new_col >= cols || new_col < 0)) {
temp_image[rows * new_col + new_row] = old_image[index];
}
}
Optimized
const unsigned ntpb = 128;
__global__ void kernel_rotate(int * old_image, int * temp_image, float rads, int rows, int cols, int half_rows, int half_cols, int rows_x_cols) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index > rows_x_cols) {
return;
}
int row = index % rows;
int col = (index - row) / rows;
float cosf_rads = __cosf(rads);
float sinf_rads = __sinf(rads);
int new_row = (int)(half_rows + ((row - half_rows) * cosf_rads) - ((col - half_cols) * sinf_rads));
int new_col = (int)(half_cols + ((row - half_rows) * sinf_rads) + ((col - half_cols) * cosf_rads));
if (!(new_row >= rows || new_row < 0 || new_col >= cols || new_col < 0)) {
temp_image[rows * new_col + new_row] = old_image[index];
}
}
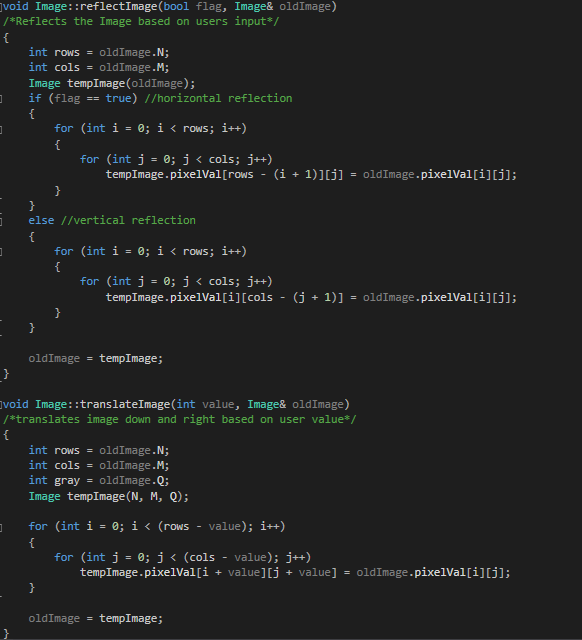
Image Reflection
Since I wasn't able to do too many big optimization techniques with the image rotation, I decided to do an additional image manipulation function. Although I still wasn't able to use shared memory to make anything faster, I was able to try one or two new things.
- Split the reflection into two kernels.
- This is the most obvious of the optimizations. Since there are two distinct operations (horizontal flip, vertical flip), it only makes sense to have one kernel for each. Each kernel would be optimized for each one. On the smallest image, the time went from 59μs to 47μs and on the largest image the time went from 711μs to 629μs.
- Only process half the image.
- This is also the other obvious optimization. Instead of going through each pixel and flipping each one to a temporary array, I would only iterate through half of them and swap each pixel with the one on the other side. There was one catch to this optimization. For the two different kernels, I had to populate my one dimensional array as either row major or column major order. This was so that the first half of index were either the top side or the left side. That way, on each of the horizontal and vertical kernels, I just had to subtract either rows or cols from a value. The memory access is also sequential. On the smallest image, the time went from 47μs to 31μs and on the largest image, the time went from 629μs to 416μs.
Kernel Speeds
Image Size
Before
After
500 x 600
59μs
31μs
800 x 800
110μs
63μs
1600 x 900
244μs
141μs
1920 x 1080
388μs
219μs
2747 x 1545
711μs
416μs
Unoptimized
__global__ void kernel_reflect(int * old_image, int * temp_image, bool flag, int rows, int cols) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index > rows * cols) {
return;
}
int row = index % rows;
int col = index / rows;
int new_row = 0;
int new_col = 0;
if (flag) {
new_row = row;
new_col = cols - col;
}
else {
new_row = rows - row;
new_col = col;
}
temp_image[rows * new_col + new_row] = old_image[index];
}
Optimized
const int reflect_ntpb = 128;
__global__ void kernel_reflect_horizontal(int * old_image, int rows, int cols, int half_cols) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index > rows * half_cols) {
return;
}
int other_index = rows * (cols - index / rows) + index % rows;
int temp = old_image[other_index];
old_image[other_index] = old_image[index];
old_image[index] = temp;
}
__global__ void kernel_reflect_vertical(int * old_image, int rows, int half_rows, int cols) {
int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index > half_rows * cols) {
return;
}
int other_index = ((rows - index / cols) * cols) + index % cols;
int temp = old_image[other_index];
old_image[other_index] = old_image[index];
old_image[index] = temp;
}
long long Image::reflectImage(bool flag, Image & source) {
int rows = source.N;
int cols = source.M;
int half_cols = cols / 2;
int half_rows = rows / 2;
int nb = 0;
if (flag)
nb = (rows * half_cols + reflect_ntpb - 1) / reflect_ntpb;
else
nb = (half_rows * cols + reflect_ntpb - 1) / reflect_ntpb;
int * d_old_image;
int * h_old_image = new int[rows * cols];
if (flag) {
for (int r = 0; r < rows; r++)
for (int c = 0; c < cols; c++)
h_old_image[rows * c + r] = source.pixelVal[r][c];
}
else {
for (int r = 0; r < rows; r++)
for (int c = 0; c < cols; c++)
h_old_image[cols * r + c] = source.pixelVal[r][c];
}
cudaMalloc((void**)&d_old_image, rows * cols * sizeof(int));
if (!d_old_image) {
cudaDeviceReset();
cout << "CUDA: out of memory (d_old_image)" << endl;
return -1;
}
high_resolution_clock::time_point first_start;
first_start = high_resolution_clock::now();
cudaMemcpy(d_old_image, h_old_image, rows * cols * sizeof(int), cudaMemcpyHostToDevice);
dim3 dGrid(nb);
dim3 dBlock(reflect_ntpb);
if (flag)
kernel_reflect_horizontal << <dGrid, dBlock >> >(d_old_image, rows, cols, half_cols);
else
kernel_reflect_vertical << <dGrid, dBlock >> >(d_old_image, rows, half_rows, cols);
cudaDeviceSynchronize();
cudaMemcpy(h_old_image, d_old_image, rows * cols * sizeof(int), cudaMemcpyDeviceToHost);
cudaDeviceSynchronize();
if (flag) {
for (int r = 0; r < rows; r++)
for (int c = 0; c < cols; c++)
source.pixelVal[r][c] = h_old_image[rows * c + r];
}
else {
for (int r = 0; r < rows; r++)
for (int c = 0; c < cols; c++)
source.pixelVal[r][c] = h_old_image[cols * r + c];
}
auto duration = duration_cast<milliseconds>(high_resolution_clock::now() - first_start);
cudaFree(d_old_image);
cudaDeviceReset();
return duration.count();
}
Conclusions
With this project, I had originally expected to get a bigger speed difference when optimizing one way or another but it turns out that it isn't so easy to do. I was never able to get any meaningful results using shared memory in these kernels because every pixel is only looked at once. My optimization benchmarks came from NSIGHT so they didn't include the code I had that created and read the 1D arrays so if I were to want to make a very fast image library, I would want to read and store data in the same way that the kernels expect it to avoid that overhead.