A-Team
Contents
Back Propagation Acceleration
Team Members
- Sebastian Djurovic, Team Lead and Developer
- Henry Leung, Developer and Quality Control
- ...
Progress
Assignment 1
Our group decided to profile a couple of different solutions, the first being a simple neural network and ray tracing solution, in order to determine the best project to generate a solution for.
Neural Network
Sebastian's findings
I found a simple neural network that takes a MNIST data set and preforms training on batches of the data. For a quick illustration MNIST is a numerical data set that contains many written numbers --in a gray scale format at 28 x 28 pixels in size. As well as the corresponding numerical values; between 0 and 9. The reason for this data set is to train networks such that they will be able to recognize written numbers when they are confront them.
Initial Profile
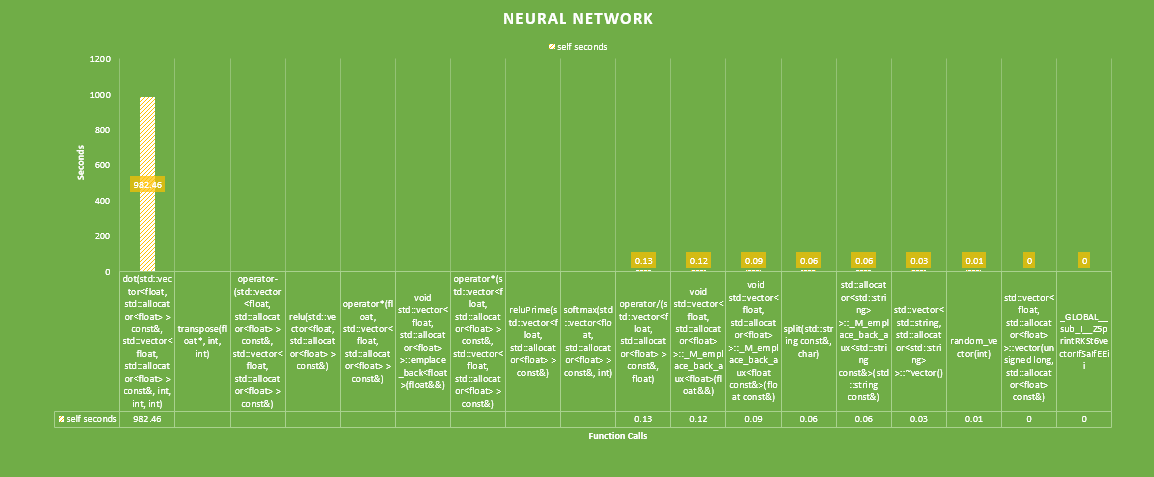
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls ns/call ns/call name 97.94 982.46 982.46 dot(std::vector<float, std::allocator<float> > const&, std::vector<float, std::allocator<float> > const&, int, int, int) 1.45 997.05 14.58 transpose(float*, int, int) 0.15 998.56 1.51 operator-(std::vector<float, std::allocator<float> > const&, std::vector<float, std::allocator<float> > const&) 0.15 1000.06 1.50 relu(std::vector<float, std::allocator<float> > const&) 0.15 1001.55 1.49 operator*(float, std::vector<float, std::allocator<float> > const&) 0.07 1002.27 0.72 519195026 1.39 1.39 void std::vector<float, std::allocator<float> >::emplace_back<float>(float&&) 0.06 1002.91 0.63 operator*(std::vector<float, std::allocator<float> > const&, std::vector<float, std::allocator<float> > const&) 0.05 1003.37 0.46 reluPrime(std::vector<float, std::allocator<float> > const&) 0.02 1003.62 0.25 softmax(std::vector<float, std::allocator<float> > const&, int) 0.01 1003.75 0.13 operator/(std::vector<float, std::allocator<float> > const&, float) 0.01 1003.87 0.12 442679 271.35 271.35 void std::vector<float, std::allocator<float> >::_M_emplace_back_aux<float>(float&&) 0.01 1003.96 0.09 13107321 6.87 6.87 void std::vector<float, std::allocator<float> >::_M_emplace_back_aux<float const&>(float const&) 0.01 1004.02 0.06 split(std::string const&, char) 0.01 1004.08 0.06 462000 130.00 130.00 void std::vector<std::string, std::allocator<std::string> >::_M_emplace_back_aux<std::string const&>(std::string const&) 0.00 1004.11 0.03 std::vector<std::string, std::allocator<std::string> >::~vector() 0.00 1004.12 0.01 random_vector(int) 0.00 1004.12 0.00 3 0.00 0.00 std::vector<float, std::allocator<float> >::vector(unsigned long, std::allocator<float> const&) 0.00 1004.12 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z5printRKSt6vectorIfSaIfEEii
After the initial profile it is obvious that the dot product function consumes 97.94% of our run time. Additionally, the transpose function also consumes 1.45% which seems messily, however during back propagation transpose is also called, as well as two rectifiers(activation functions), reluPrime and relu.
// Back propagation
vector<float> dyhat = (yhat - b_y);
// dW3 = a2.T * dyhat
vector<float> dW3 = dot(transpose( &a2[0], BATCH_SIZE, 64 ), dyhat, 64, BATCH_SIZE, 10);
// dz2 = dyhat * W3.T * relu'(a2)
vector<float> dz2 = dot(dyhat, transpose( &W3[0], 64, 10 ), BATCH_SIZE, 10, 64) * reluPrime(a2);
// dW2 = a1.T * dz2
vector<float> dW2 = dot(transpose( &a1[0], BATCH_SIZE, 128 ), dz2, 128, BATCH_SIZE, 64);
// dz1 = dz2 * W2.T * relu'(a1)
vector<float> dz1 = dot(dz2, transpose( &W2[0], 128, 64 ), BATCH_SIZE, 64, 128) * reluPrime(a1);
// dW1 = X.T * dz1
vector<float> dW1 = dot(transpose( &b_X[0], BATCH_SIZE, 784 ), dz1, 784, BATCH_SIZE, 128);
vector <float> dot (const vector <float>& m1, const vector <float>& m2, const int m1_rows, const int m1_columns, const int m2_columns) {
/* Returns the product of two matrices: m1 x m2.
Inputs:
m1: vector, left matrix of size m1_rows x m1_columns
m2: vector, right matrix of size m1_columns x m2_columns (the number of rows in the right matrix
must be equal to the number of the columns in the left one)
m1_rows: int, number of rows in the left matrix m1
m1_columns: int, number of columns in the left matrix m1
m2_columns: int, number of columns in the right matrix m2
Output: vector, m1 * m2, product of two vectors m1 and m2, a matrix of size m1_rows x m2_columns
*/
vector <float> output (m1_rows*m2_columns);
for( int row = 0; row != m1_rows; ++row ) {
for( int col = 0; col != m2_columns; ++col ) {
output[ row * m2_columns + col ] = 0.f;
for( int k = 0; k != m1_columns; ++k ) {
output[ row * m2_columns + col ] += m1[ row * m1_columns + k ] * m2[ k * m2_columns + col ];
}
}
}
return output;
}