Happy Valley
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
[hide]Project Name Goes here
Team Members
- Yalong Li, Pilot
- Olga Belavina, Pilot Lieutenant
Assignment 1
LZSS
LZSS (Lempel–Ziv–Storer–Szymanski) is a compression algorithm that belongs to LZ77 family. It attempts to replace a string of symbols with a reference to a dictionary location of the same string.
The C implementation includes both compression and un-compression functionalities, however only compression algorithm will be tested and profiled. The source code for LZSS an be found here.
Data Overview
Supplying dummy text file to the compression function may not reflect real-world performance. Meaningful data needs to be used for the compression algorithm bench-marking and profiling since randomly generated text does not follow language rules/patterns (meaning it’s harder to compress such data).
The CIA world fact book was used as our test material. The file itself is only 4 megabytes, so in order to benchmark LZSS for larger size, world fact book text was concatenated to itself (many times) to reach certain size.
| File Name | Size (MB) |
|---|---|
| 1GB.txt | 1071 |
| 500M.txt | 536 |
| 250M.txt | 268 |
| 125M.txt | 134 |
Profiling
Binary was produced (for both debugging and profiling) with gcc command. Code snippet below demonstrates profiling commands used for 250 megabyte file (same logic was applied to other text files). The binary is supplied with the original text file as its first argument and destination file for the compressed output.
[obelavina@localhost gpu610]$ gcc lzss.c -o lzss [obelavina@localhost gpu610]$ ./lzss c 250M.txt 250M.compressed In : 280730901 bytes Out: 149085687 bytes Out/In: 0.531 [obelavina@localhost gpu610]$ gprof -p -b lzss > 250M.flt
GPROF Result
/////////////////// 125MB FILE /////////////////// [obelavina@localhost gpu610]$ cat 125M.flt Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 82.23 22.73 22.73 140365467 0.00 0.00 insert_node 11.29 25.85 3.12 140365451 0.00 0.00 delete_node 6.58 27.67 1.82 1 1.82 27.69 compress 0.07 27.69 0.02 1 0.02 0.02 init_tree
/////////////////// 250MB FILE /////////////////// [obelavina@localhost gpu610]$ cat 250M.flt Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 83.53 43.49 43.49 280730917 0.00 0.00 insert_node 10.42 48.92 5.43 280730901 0.00 0.00 delete_node 6.08 52.09 3.17 1 3.17 52.13 compress 0.08 52.13 0.04 1 0.04 0.04 init_tree /////////////////// 500MB FILE /////////////////// [obelavina@localhost gpu610]$ cat 500M.flt Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 83.61 87.34 87.34 561461817 0.00 0.00 insert_node 10.82 98.64 11.30 561461801 0.00 0.00 delete_node 5.58 104.46 5.83 1 5.83 104.55 compress 0.09 104.55 0.09 1 0.09 0.09 init_tree /////////////////// 1GB FILE /////////////////// [obelavina@localhost gpu610]$ cat 1G.flt Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 83.59 175.05 175.05 1122923616 0.00 0.00 insert_node 10.60 197.26 22.21 1122923600 0.00 0.00 delete_node 5.81 209.44 12.18 1 12.18 209.69 compress 0.12 209.69 0.25 1 0.25 0.25 init_tree
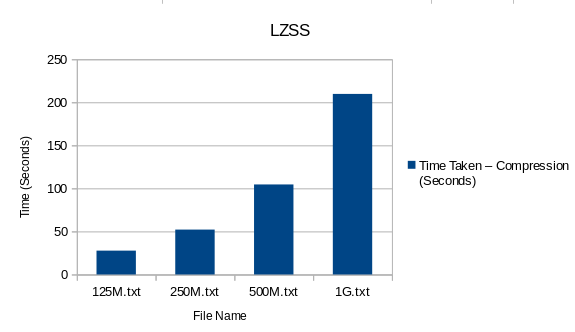
Plotted Result
| File Name | File Size (MB) | Total Time Taken – Compression (Seconds) |
|---|---|---|
| 125M.txt | 134 | 27.69 |
| 250M.txt | 268 | 52.13 |
| 500M.txt | 536 | 104.55 |
| 1G.txt | 1071 | 209.69 |
Analysis
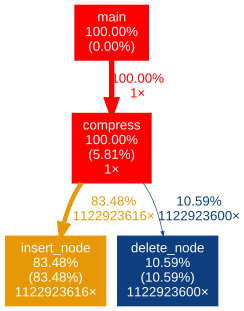
Lets first try to visualise the function calls so it is easier to determine where LZSS algorithm spends most of the time.
gprof ./lzss | gprof2dot | dot | convert - out.png
The call graph demonstrates that insert_node function takes the bulk of work (83.48%). delete_node takes only 10% even though it’s called nearly as many times as insert_node. It is hard to determine if LZSS is a good candidate for GPU optimisation: data throughput can be quite large but the logic of the algorithm includes some branching which can introduce some issues while porting code to CUDA. I suspect that compress function itself will need to be parallized (rather than insert_node).
Resources:
The data source (The Large Corpus): http://corpus.canterbury.ac.nz/descriptions/#cantrbry
LZSS Source Code: http://my.execpc.com/~geezer/code/lzss.c
SelectionSort
Selection Sort algorithm loops through every value in an array and finds the minimum values, assuming sort in ascending order, then puts it to the sorted area.
Source Code
// C program for implementation of selection sort
#include <stdio.h>
#include<cstdlib>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
swap(&arr[min_idx], &arr[i]);
}
}
// Driver program to test above functions
int main()
{
int arrSize = 150000;
int arr[arrSize];
for (int i = 0; i < arrSize; i++) {
arr[i] = rand() % 10000 + 1;
}
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
return 0;
}
gprof results
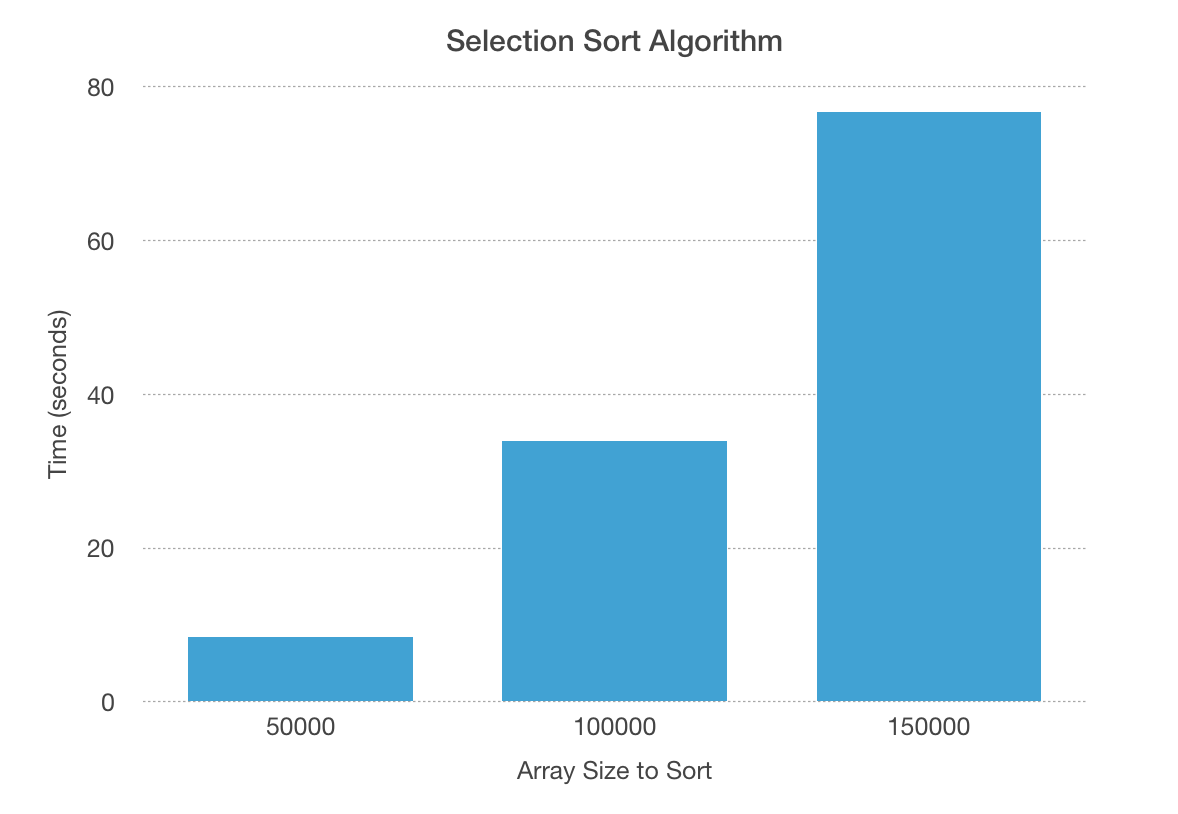
Tested the selection sort algorithm with three different array size: 50000, 100000, and 150000. The amount of time spent increased noticeably.
// Array Size 50000
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
100.00 8.45 8.45 1 8.45 8.45 selectionSort(int*, int)
0.00 8.45 0.00 49999 0.00 0.00 swap(int*, int*)
granularity: each sample hit covers 4 byte(s) for 0.12% of 8.45 seconds
index % time self children called name
<spontaneous>
[1] 100.0 0.00 8.45 main [1]
8.45 0.00 1/1 selectionSort(int*, int) [2]
-----------------------------------------------
8.45 0.00 1/1 main [1]
[2] 100.0 8.45 0.00 1 selectionSort(int*, int) [2]
0.00 0.00 49999/49999 swap(int*, int*) [6]
-----------------------------------------------
0.00 0.00 49999/49999 selectionSort(int*, int) [2]
[6] 0.0 0.00 0.00 49999 swap(int*, int*) [6]
-----------------------------------------------
// Array Size 100000
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
100.00 33.96 33.96 1 33.96 33.96 selectionSort(int*, int)
0.00 33.96 0.00 99999 0.00 0.00 swap(int*, int*)
granularity: each sample hit covers 4 byte(s) for 0.03% of 33.96 seconds
index % time self children called name
<spontaneous>
[1] 100.0 0.00 33.96 main [1]
33.96 0.00 1/1 selectionSort(int*, int) [2]
-----------------------------------------------
33.96 0.00 1/1 main [1]
[2] 100.0 33.96 0.00 1 selectionSort(int*, int) [2]
0.00 0.00 99999/99999 swap(int*, int*) [6]
-----------------------------------------------
0.00 0.00 99999/99999 selectionSort(int*, int) [2]
[6] 0.0 0.00 0.00 99999 swap(int*, int*) [6]
-----------------------------------------------
// Array Size 150000
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
99.99 76.65 76.65 1 76.65 76.66 selectionSort(int*, int)
0.01 76.66 0.01 149999 0.00 0.00 swap(int*, int*)
granularity: each sample hit covers 4 byte(s) for 0.01% of 76.66 seconds
index % time self children called name
<spontaneous>
[1] 100.0 0.00 76.66 main [1]
76.65 0.01 1/1 selectionSort(int*, int) [2]
-----------------------------------------------
76.65 0.01 1/1 main [1]
[2] 100.0 76.65 0.01 1 selectionSort(int*, int) [2]
0.01 0.00 149999/149999 swap(int*, int*) [3]
-----------------------------------------------
0.01 0.00 149999/149999 selectionSort(int*, int) [2]
[3] 0.0 0.01 0.00 149999 swap(int*, int*) [3]
-----------------------------------------------
Result in chart diagram
Reference
code website: https://www.geeksforgeeks.org/selection-sort/
Bitonic Sort
Bitonic Sort is a classic parallel algorithm for sorting.
Source Code
void bitonic_sort(int *data, int N)
{
int i, j, k;
int temp;
for (k = 2; k <= N; k = 2 * k)
{
for (j = k >> 1; j>0; j = j >> 1)
{
for (i = 0; i<N; i++)
{
int ixj = i^j;
if ((ixj)>i)
{
if ((i&k) == 0 && data[i] > data[ixj]) {
temp = data[i];
data[i] = data[ixj];
data[ixj] = temp;
}
if ((i&k) != 0 && data[i] < data[ixj]) {
temp = data[i];
data[i] = data[ixj];
data[ixj] = temp;
}
}
}
}
}
}
gprof results
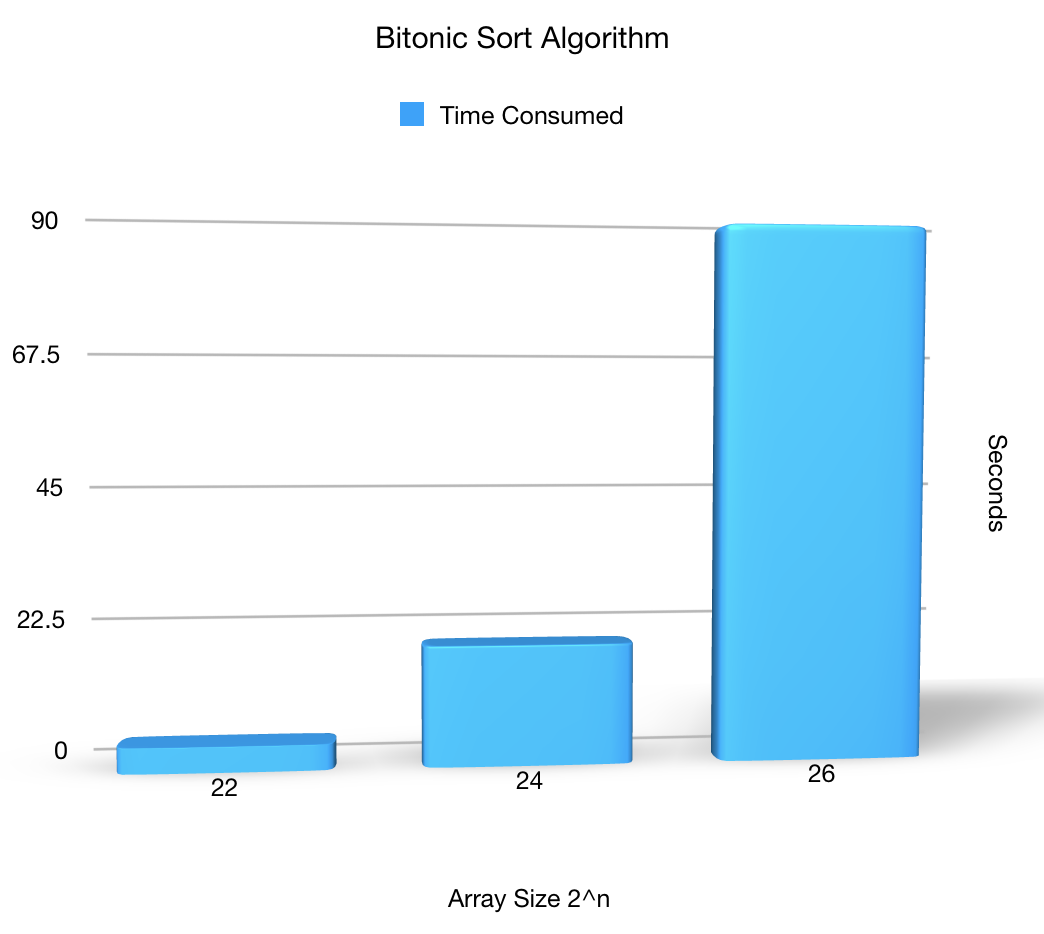
Tested the Bitonic sort with three different array size: 4194304, 16777216, and 67108864.
// Array Size 2^22 = 4194304 Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 100.00 4.20 4.20 bitonic_sort(int*, int) 0.00 4.20 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z12bitonic_sortPii
// Array Size 2^24 = 16777216 Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 100.00 19.84 19.84 bitonic_sort(int*, int) 0.00 19.84 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z12bitonic_sortPii
// Array Size 2^26 = 67108864 Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 100.00 88.26 88.26 bitonic_sort(int*, int) 0.00 88.26 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z12bitonic_sortPii
Result in chart diagram
Reference
https://www.geeksforgeeks.org/bitonic-sort/