Difference between revisions of "Kernal Blas"
(→Assignment 3) |
(→Assignment 3) |
||
| Line 216: | Line 216: | ||
=== Assignment 3 === | === Assignment 3 === | ||
The code we used to optimize our code | The code we used to optimize our code | ||
| − | < | + | <syntaxhighlight lang="cpp"> |
#include <stdlib.h> | #include <stdlib.h> | ||
#include <stdio.h> | #include <stdio.h> | ||
| Line 296: | Line 296: | ||
return 0; | return 0; | ||
} | } | ||
| − | </ | + | </syntaxhighlight> |
How we optimize and improved the code is instead of using a randomized number we ask the user for input on pi calculation. | How we optimize and improved the code is instead of using a randomized number we ask the user for input on pi calculation. | ||
Revision as of 19:22, 1 April 2018
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
Kernal Blas
Team Members
Progress
Assignment 1
Calculation of Pi
For this assessment, we used code found at helloacm.com
In this version, the value of PI is calculated using the Monte Carlo method. This method states:
- A circle with radius r in a squre with side length 2r
- The area of the circle is Πr2 and the area of the square is 4r2
- The ratio of the area of the circle to the area of the square is: Πr2 / 4r2 = Π / 4
- If you randomly generate N points inside the square, approximately N * Π / 4 of those points (M) should fall inside the circle.
- Π is then approximated as:
- N * Π / 4 = M
- Π / 4 = M / N
- Π = 4 * M / N
For simplicity the radius of the circle is 1. With this, we randomly generate points within the area and count the number of times each point falls within the circle, between 0 and 1. We then calculate the ratio and multiply by 4 which will give us the approximation of Π.
When we run the program we see:
1st Run
1000 3.152 - took - 0 millisecs 10000 3.1328 - took - 0 millisecs 100000 3.14744 - took - 9 millisecs 1000000 3.141028 - took - 96 millisecs 10000000 3.1417368 - took - 998 millisecs 100000000 3.1419176 - took - 10035 millisecs The first column represents the "stride" or the number of digits of pi we are calculating to.
With this method, we can see that the accuracy of the calculation is slightly off. This is due to the randomization of points within the circle. Running the program again will give us slightly different results.
2nd Run
1000 3.12 - took - 0 millisecs 10000 3.1428 - took - 0 millisecs 100000 3.13528 - took - 9 millisecs 1000000 3.143348 - took - 106 millisecs 10000000 3.1414228 - took - 1061 millisecs 100000000 3.14140056 - took - 8281 millisecs
The hotspot within the code lies in the loops. There iteration for the loops is O(n2)
Potential Speedup:
Using Gustafson's Law:
P = 50% of the code P = 0.50 n = ? S(n)= n - ( 1 - P ) ∙ ( n - 1 ) Sn = n - ( 1 - .5 ) ∙ ( n - 1 ) Sn =
Data Compression
For this suggested project we used the LZW algorithm from one of the suggested projects.
The compress dictionary copies the file into a new file with a .LZW filetype which uses ASCII
The function that compresses the file initializing with ASCII
void compress(string input, int size, string filename) {
unordered_map<string, int> compress_dictionary(MAX_DEF);
//Dictionary initializing with ASCII
for (int unsigned i = 0; i < 256; i++) {
compress_dictionary[string(1, i)] = i;
}
string current_string;
unsigned int code;
unsigned int next_code = 256;
//Output file for compressed data
ofstream outputFile;
outputFile.open(filename + ".lzw");
for (char& c : input) {
current_string = current_string + c;
if (compress_dictionary.find(current_string) == compress_dictionary.end()) {
if (next_code <= MAX_DEF)
compress_dictionary.insert(make_pair(current_string, next_code++));
current_string.erase(current_string.size() - 1);
outputFile << convert_int_to_bin(compress_dictionary[current_string]);
current_string = c;
}
}
if (current_string.size())
outputFile << convert_int_to_bin(compress_dictionary[current_string]);
outputFile.close();
}
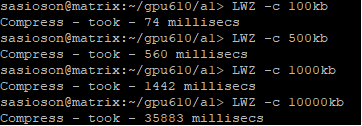
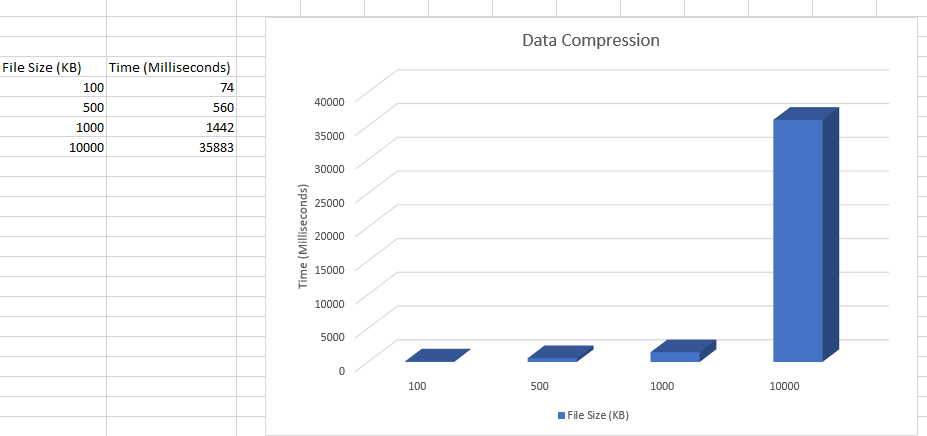
The results of the compression from:
Parallelizing
From one of the suggested improvements in the algorithm post link. A potential improvement is changing from char& c to a const char in the for loop
for (char& c : input) {since char& c is not being modified.
Assignment 2
In order to parallelize the code from above, we decided to use a kernel to handle the calculations.
The logic remains the same but the results are much faster.
Offloading to the GPU results in a pi calculation time to be reduced

Kernel code used
__global__ void calculate(float *sum, int nbin, float step, int nthreads, int nblocks) {
int i;
float x;
int idx = blockIdx.x * blockDim.x + threadIdx.x; // Sequential thread index across the blocks
for (i = idx; i< nbin; i += nthreads*nblocks) {
x = (i + 0.5)*step;
sum[idx] += 4.0 / (1.0 + x*x);
}
}
Main function
// Main routine that executes on the host
int main(int argc, char** argv) {
// interpret command-line argument
if (argc != 2) {
std::cerr << argv[0] << ": invalid number of arguments\n";
return 1;
}
float n = std::atoi(argv[1]);
int nblocks = 30;
steady_clock::time_point ts, te;
dim3 dimGrid(nblocks, 1, 1); // Grid dimensions
dim3 dimBlock(ntpb, 1, 1); // Block dimensions
float *sumHost, *sumDev; // Pointer to host & device arrays
float step = 1.0 / n; // Step size
size_t size = nblocks*ntpb * sizeof(float); //Array memory size
sumHost = (float *)malloc(size); // Allocate array on host
cudaMalloc((void **)&sumDev, size); // Allocate array on device
// Initialize array in device to 0
cudaMemset(sumDev, 0, size);
// initialization
std::srand(std::time(nullptr));
ts = steady_clock::now();
// Do calculation on device
calculate << <dimGrid, dimBlock >> > (sumDev, n, step, ntpb, nblocks); // call CUDA kernel
te = steady_clock::now();
cudaMemcpy(sumHost, sumDev, size, cudaMemcpyDeviceToHost);
for (tid = 0; tid<ntpb*nblocks; tid++)
pi += sumHost[tid];
pi *= step;
// Print results
printf("Number of iterations= %f\nPI = %f\n", n,pi);
reportTime("Pi calculation took ", te - ts);
// Cleanup
free(sumHost);
cudaFree(sumDev);
return 0;
}Results CPU vs GPU
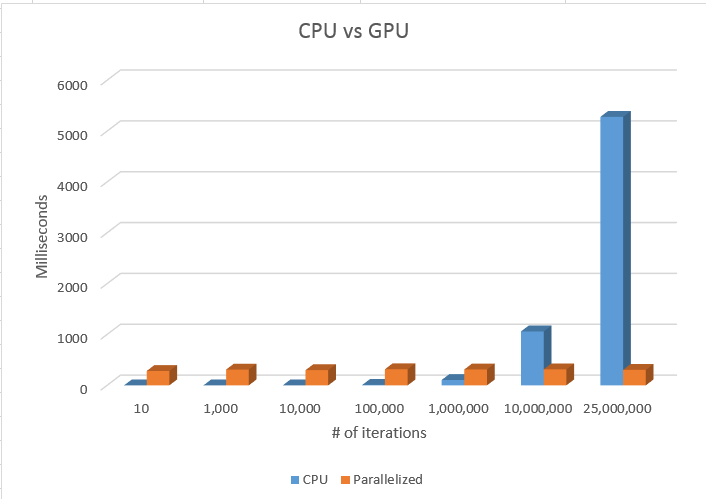
As we can see above, the more iterations, the more accurate the calculation of PI.
The CPU's results drastically change as we increase the iteration 10x.
However, the parallelized results seem to stay accurate throughout the iterations.
As the iteration passes 100 million, we have a bit of memory leaks which results in inaccurate results.
Assignment 3
The code we used to optimize our code
#include <stdlib.h>
#include <stdio.h>
#include <cuda.h>
#include <math.h>
#include <time.h>
#include <curand_kernel.h>
#include <cstdlib>
#define BLOCKS 30
#define THREADS 8
#define PI 3.1415926535 // known value of pi
__global__ void gpu_monte_carlo(float *estimate, curandState *states, float n) {
unsigned int tid = threadIdx.x + blockDim.x * blockIdx.x;
float points_in_circle = 0;
float x, y;
curand_init(1234, tid, 0, &states[tid]); // Initialize CURAND
for (int i = 0; i < n; i++) {
x = curand_uniform(&states[tid]);
y = curand_uniform(&states[tid]);
points_in_circle += (x*x + y*y <= 1.0f); // count if x & y is in the circle.
}
estimate[tid] = 4.0f * points_in_circle / n; // return estimate of pi
}
float host_monte_carlo(long trials) {
float x, y;
long points_in_circle = 0;
for (long i = 0; i < trials; i++) {
x = rand() / (float)RAND_MAX;
y = rand() / (float)RAND_MAX;
points_in_circle += (x*x + y*y <= 1.0f);
}
return 4.0f * points_in_circle / trials;
}
int main(int argc, char** argv) {
clock_t start, stop;
curandState *devStates;
float n = std::atoi(argv[1]);
dim3 dimGrid(BLOCKS, 1, 1); // Grid dimensions
dim3 dimBlock(THREADS, 1, 1); // Block dimensions
float *dev, *host;
size_t size = BLOCKS * THREADS* sizeof(float); //Array memory size
printf("# of trials per thread = %.0f, # of blocks = %d, # of threads/block = %d.\n", n,
BLOCKS, THREADS);
start = clock();
host = (float *)malloc(size); // Allocate array on host
cudaMalloc((void **)&dev, size); // Allocate array on device
cudaMemset(dev, 0, size);
cudaMalloc((void **)&devStates, THREADS * BLOCKS * sizeof(curandState));
gpu_monte_carlo << <BLOCKS, THREADS >> >(dev, devStates, n);
cudaMemcpy(host, dev, size, cudaMemcpyDeviceToHost); // return results
float pi_gpu = 0.0f;
for (int i = 0; i < BLOCKS * THREADS; i++) {
pi_gpu += host[i];
}
pi_gpu /= (BLOCKS * THREADS);
stop = clock();
printf("GPU pi calculated in %f s.\n", (stop - start) / (float)CLOCKS_PER_SEC);
start = clock();
//float pi_cpu = host_monte_carlo(BLOCKS * THREADS * n);
stop = clock();
printf("CPU pi calculated in %f s.\n", (stop - start) / (float)CLOCKS_PER_SEC);
printf("CUDA estimate of PI = %f [error of %f]\n", pi_gpu, pi_gpu - PI);
//printf("CPU estimate of PI = %f [error of %f]\n", pi_cpu, pi_cpu - PI);
return 0;
}How we optimize and improved the code is instead of using a randomized number we ask the user for input on pi calculation.