Difference between revisions of "BLAStoise"
(→Assignment 1) |
(→Assignment 1) |
||
| Line 445: | Line 445: | ||
If we run the program for a larger sequence of 50000, the following flat profile is generated. | If we run the program for a larger sequence of 50000, the following flat profile is generated. | ||
| − | Flat profile: | + | Flat profile: |
| − | Each sample counts as 0.01 seconds. | + | Each sample counts as 0.01 seconds. |
% cumulative self self total | % cumulative self self total | ||
time seconds seconds calls s/call s/call name | time seconds seconds calls s/call s/call name | ||
| Line 540: | Line 540: | ||
</pre> | </pre> | ||
| − | Within the function itself there are many nested calls to the sumSteps function in the SubmatrixCalculator.cpp file. Since the purpose of this function is to retrieve the path through the matrix while calculating the number of steps, this simple operation could benefit from the usage of a GPU rather than a CPU. | + | Within the function itself there are many nested loops with calls to the sumSteps function in the SubmatrixCalculator.cpp file. Since the purpose of this function is to retrieve the path through the matrix while calculating the number of steps, this simple operation could benefit from the usage of a GPU rather than a CPU. |
=== Assignment 2 === | === Assignment 2 === | ||
=== Assignment 3 === | === Assignment 3 === | ||
Revision as of 19:41, 12 February 2017
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
Project Name Goes here
Team Members
- Matt Babol, Sudoku
- Jonathan Desmond, Oil Painting
- Sallie Jiang, Some other responsibility
_
_,..-"""--' `,.-".
,' __.. --', |
_/ _.-"' | .' | | ____
,.-""' `-"+.._| `.' | `-..,',--.`.
| ,. ' j 7 l \__
|.-' /| | j|| .
`. | / L`.`""','|\ \
`.,----..._ ,'`"'-. ,' \ `""' | | l
Y `-----' v' ,'`,.__..' | .
`. / / / `.| |
`. / l j ,^. |L
`._ L +. |._ .' \| | \
.`--...__,..-'""'-._ l L """ | | \
.' ,`-......L_ \ \ \ _.' ,'. l
,-"`. / ,-.---.' `. \ L..--"' _.-^.| l
.-"".'"`. Y `._' ' `. | | _,.--'" | |
`._' | |,-'| l `. | |".. | l
,'. | |`._' | `. | |_,...---"""""` L
/ | j _|-' `. L | j ,| | |
`-,"._,-+' /`---^..../._____,.L',' `. |\ |
|,' L | `-. | \j
. \ `, | |
\ __`.Y._ -. j |
\ _.,' `._ \ | j
,-"`-----""""' |`. \ 7 |
/ `. ' | \ \ / |
| ` / | \ Y |
| \ . ,' | L_.-')
L `. | / ] _.-^._
\ ,' `-7 ,-' / | ,' `-._
_,`._ `. _,-' ,',^.- `.
,-' v.... _.`"', _:'--....._______,.-'
._______./ /',,-'"'`'--. ,-' `.
"""""`.,' _\`----...'
--------""'
Progress
Assignment 1
Sudoku Solver by Matt B.
Sudoku solver is a program that solves a sudoku puzzle. The user can input an existing file and have the program solve this, or can manually enter values to be solved. The sudoku puzzle is 9x9 in size. The data needs to be in a specific format for the program to work. There are 9 rows of values, with each cell/element in the row needing to be separated by a space. A value of 0 tells the program to solve this value.
Original source code can be found here.
Easy puzzle
To compile the program, open the terminal and go to the projects directory
$ g++ -std=c++0x -pg solver.cpp checks.cpp checksolution.cpp -o Sudoku
This will create an executable file called Sudoku. -pg is used for creating a gmon.out file, which will allow us to profile the program with arguments.
This is the easy sudoku puzzle that will be running through the program first. The file is saved as 'puzzle' in the same directory.
0 6 0 0 0 0 9 7 2 0 5 0 0 0 2 0 0 3 0 7 0 3 9 0 5 0 0 2 0 0 0 0 5 4 0 8 0 0 0 0 0 0 0 0 0 3 0 1 8 0 0 0 0 6 0 0 4 0 2 3 0 8 0 7 0 0 9 0 0 0 2 0 9 2 5 0 0 0 0 4 0
Run the code with
$ ./Sudoku puzzle
After the program is done running, the result is
1 6 3 4 5 8 9 7 2 4 5 9 7 1 2 8 6 3 8 7 2 3 9 6 5 1 4 2 9 7 1 6 5 4 3 8 5 8 6 2 3 4 1 9 7 3 4 1 8 7 9 2 5 6 6 1 4 5 2 3 7 8 9 7 3 8 9 4 1 6 2 5 9 2 5 6 8 7 3 4 1
Test Case
To profile the program, run this command.
$ gprof -p -b ./Sudoku gmon.out > Sudoku.flt
The profiling result
Flat profile: Each sample counts as 0.01 seconds. no time accumulated % cumulative self self total time seconds seconds calls Ts/call Ts/call name 0.00 0.00 0.00 4539 0.00 0.00 checkRow(int, int) 0.00 0.00 0.00 1620 0.00 0.00 checkColumn(int, int) 0.00 0.00 0.00 1120 0.00 0.00 placeNum(int, int) 0.00 0.00 0.00 698 0.00 0.00 checkSquare(int, int, int) 0.00 0.00 0.00 476 0.00 0.00 goBack(int&, int&) 0.00 0.00 0.00 2 0.00 0.00 print(int (*) [9]) 0.00 0.00 0.00 1 0.00 0.00 _GLOBAL__sub_I_sudoku 0.00 0.00 0.00 1 0.00 0.00 _GLOBAL__sub_I_temp 0.00 0.00 0.00 1 0.00 0.00 solveSudoku() 0.00 0.00 0.00 1 0.00 0.00 storePositions() 0.00 0.00 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 0.00 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
Call graph
granularity: each sample hit covers 2 byte(s) no time propagated
index % time self children called name
0.00 0.00 4539/4539 placeNum(int, int) [10]
[8] 0.0 0.00 0.00 4539 checkRow(int, int) [8]
-----------------------------------------------
0.00 0.00 1620/1620 placeNum(int, int) [10]
[9] 0.0 0.00 0.00 1620 checkColumn(int, int) [9]
-----------------------------------------------
0.00 0.00 1120/1120 solveSudoku() [16]
[10] 0.0 0.00 0.00 1120 placeNum(int, int) [10]
0.00 0.00 4539/4539 checkRow(int, int) [8]
0.00 0.00 1620/1620 checkColumn(int, int) [9]
0.00 0.00 698/698 checkSquare(int, int, int) [11]
-----------------------------------------------
0.00 0.00 698/698 placeNum(int, int) [10]
[11] 0.0 0.00 0.00 698 checkSquare(int, int, int) [11]
-----------------------------------------------
0.00 0.00 476/476 solveSudoku() [16]
[12] 0.0 0.00 0.00 476 goBack(int&, int&) [12]
-----------------------------------------------
0.00 0.00 2/2 main [6]
[13] 0.0 0.00 0.00 2 print(int (*) [9]) [13]
-----------------------------------------------
0.00 0.00 1/1 __libc_csu_init [30]
[14] 0.0 0.00 0.00 1 _GLOBAL__sub_I_sudoku [14]
0.00 0.00 1/1 __static_initialization_and_destruction_0(int, int) [18]
-----------------------------------------------
0.00 0.00 1/1 __libc_csu_init [30]
[15] 0.0 0.00 0.00 1 _GLOBAL__sub_I_temp [15]
0.00 0.00 1/1 __static_initialization_and_destruction_0(int, int) [19]
-----------------------------------------------
0.00 0.00 1/1 main [6]
[16] 0.0 0.00 0.00 1 solveSudoku() [16]
0.00 0.00 1120/1120 placeNum(int, int) [10]
0.00 0.00 476/476 goBack(int&, int&) [12]
-----------------------------------------------
0.00 0.00 1/1 main [6]
[17] 0.0 0.00 0.00 1 storePositions() [17]
-----------------------------------------------
0.00 0.00 1/1 _GLOBAL__sub_I_sudoku [14]
[18] 0.0 0.00 0.00 1 __static_initialization_and_destruction_0(int, int) [18]
-----------------------------------------------
0.00 0.00 1/1 _GLOBAL__sub_I_temp [15]
[19] 0.0 0.00 0.00 1 __static_initialization_and_destruction_0(int, int) [19]
-----------------------------------------------
Index by function name
[14] _GLOBAL__sub_I_sudoku [16] solveSudoku() [13] print(int (*) [9])
[15] _GLOBAL__sub_I_temp [17] storePositions() [12] goBack(int&, int&)
[9] checkColumn(int, int) [18] __static_initialization_and_destruction_0(int, int) [8] checkRow(int, int)
[11] checkSquare(int, int, int) [19] __static_initialization_and_destruction_0(int, int) [10] placeNum(int, int)
Analysis
The analysis reveals that the program took no time in solving this puzzle. However, the function checkRow and checkColumn were called the most. These two functions are used for checking whether the row and columns are correct. For a deeper analysis, a harder puzzle must be used.
Hard puzzle
For the hard puzzle, below is the input file as well as the result
0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 8 5 0 0 1 0 2 0 0 0 0 0 0 0 5 0 7 0 0 0 0 0 4 0 0 0 1 0 0 0 9 0 0 0 0 0 0 0 5 0 0 0 0 0 0 7 3 0 0 2 0 1 0 0 0 0 0 0 0 0 4 0 0 0 9 9 8 7 6 5 4 3 2 1 2 4 6 1 7 3 9 8 5 3 5 1 9 2 8 7 4 6 1 2 8 5 3 7 6 9 4 6 3 4 8 9 2 1 5 7 7 9 5 4 6 1 8 3 2 5 1 9 2 8 6 4 7 3 4 7 2 3 1 9 5 6 8 8 6 3 7 4 5 2 1 9
The profiling results are
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 45.34 7.76 7.76 622577597 0.00 0.00 checkRow(int, int) 18.63 10.94 3.19 223365661 0.00 0.00 checkColumn(int, int) 14.38 13.40 2.46 157353814 0.00 0.00 placeNum(int, int) 13.24 15.67 2.27 100608583 0.00 0.00 checkSquare(int, int, int) 4.80 16.49 0.82 69175252 0.00 0.00 goBack(int&, int&) 3.46 17.08 0.59 1 0.59 17.08 solveSudoku() 0.29 17.13 0.05 1 0.05 0.05 _GLOBAL__sub_I_sudoku 0.00 17.13 0.00 2 0.00 0.00 print(int (*) [9]) 0.00 17.13 0.00 1 0.00 0.00 _GLOBAL__sub_I_temp 0.00 17.13 0.00 1 0.00 0.00 storePositions() 0.00 17.13 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int) 0.00 17.13 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)
Call graph
granularity: each sample hit covers 2 byte(s) for 0.06% of 17.13 seconds
index % time self children called name
<spontaneous>
[1] 99.7 0.00 17.08 main [1]
0.59 16.49 1/1 solveSudoku() [2]
0.00 0.00 2/2 print(int (*) [9]) [16]
0.00 0.00 1/1 storePositions() [18]
-----------------------------------------------
0.59 16.49 1/1 main [1]
[2] 99.7 0.59 16.49 1 solveSudoku() [2]
2.46 13.21 157353814/157353814 placeNum(int, int) [3]
0.82 0.00 69175252/69175252 goBack(int&, int&) [7]
-----------------------------------------------
2.46 13.21 157353814/157353814 solveSudoku() [2]
[3] 91.5 2.46 13.21 157353814 placeNum(int, int) [3]
7.76 0.00 622577597/622577597 checkRow(int, int) [4]
3.19 0.00 223365661/223365661 checkColumn(int, int) [5]
2.27 0.00 100608583/100608583 checkSquare(int, int, int) [6]
-----------------------------------------------
7.76 0.00 622577597/622577597 placeNum(int, int) [3]
[4] 45.3 7.76 0.00 622577597 checkRow(int, int) [4]
-----------------------------------------------
3.19 0.00 223365661/223365661 placeNum(int, int) [3]
[5] 18.6 3.19 0.00 223365661 checkColumn(int, int) [5]
-----------------------------------------------
2.27 0.00 100608583/100608583 placeNum(int, int) [3]
[6] 13.2 2.27 0.00 100608583 checkSquare(int, int, int) [6]
-----------------------------------------------
0.82 0.00 69175252/69175252 solveSudoku() [2]
[7] 4.8 0.82 0.00 69175252 goBack(int&, int&) [7]
-----------------------------------------------
0.05 0.00 1/1 __libc_csu_init [9]
[8] 0.3 0.05 0.00 1 _GLOBAL__sub_I_sudoku [8]
0.00 0.00 1/1 __static_initialization_and_destruction_0(int, int) [19]
-----------------------------------------------
<spontaneous>
[9] 0.3 0.00 0.05 __libc_csu_init [9]
0.05 0.00 1/1 _GLOBAL__sub_I_sudoku [8]
0.00 0.00 1/1 _GLOBAL__sub_I_temp [17]
-----------------------------------------------
0.00 0.00 2/2 main [1]
[16] 0.0 0.00 0.00 2 print(int (*) [9]) [16]
-----------------------------------------------
0.00 0.00 1/1 __libc_csu_init [9]
[17] 0.0 0.00 0.00 1 _GLOBAL__sub_I_temp [17]
0.00 0.00 1/1 __static_initialization_and_destruction_0(int, int) [20]
-----------------------------------------------
0.00 0.00 1/1 main [1]
[18] 0.0 0.00 0.00 1 storePositions() [18]
-----------------------------------------------
0.00 0.00 1/1 _GLOBAL__sub_I_sudoku [8]
[19] 0.0 0.00 0.00 1 __static_initialization_and_destruction_0(int, int) [19]
-----------------------------------------------
0.00 0.00 1/1 _GLOBAL__sub_I_temp [17]
[20] 0.0 0.00 0.00 1 __static_initialization_and_destruction_0(int, int) [20]
-----------------------------------------------
Index by function name
[8] _GLOBAL__sub_I_sudoku [2] solveSudoku() [16] print(int (*) [9])
[17] _GLOBAL__sub_I_temp [18] storePositions() [7] goBack(int&, int&)
[5] checkColumn(int, int) [19] __static_initialization_and_destruction_0(int, int) [4] checkRow(int, int)
[6] checkSquare(int, int, int) [20] __static_initialization_and_destruction_0(int, int) [3] placeNum(int, int)
Analysis
With a harder puzzle, the time for the program to solve the puzzle increased significantly. The total time to complete this puzzle was 17.13 seconds. The program spends almost half of its running time checking if the row is correct, and another 18% of its time checking whether the column is correct. This program contains thousands of calls to check the row and column values, this is why the program would be excellent project for parallelizing.
Oil Painting By Sallie J.
This program converts a regular image into a stylized oil painting, it uses OpenCV. The painting algorithm depends on the brush size and colour intensity. The program takes three command line arguments: int for brush size, int for intensity and file name of an image. Upon finishing, the program produces the original image along with the oil paint version and the total time required in seconds.
The original source code can be found here.
However there have been some changes to make testing and profiling slightly easier. (Mainly changes are putting the for-loop logic into a function outside of the main and modifying for command line arguments instead of hard coding values.)
Running the program
To compile the program on Linux you must download the OpenCV library and then create a makefile that will create the executable OilPaint.exe. To compile the program in visual studio you will need to set project properties for OpenCV through setting the C/C++ Additional Include Directories, Linker Additional Library Directories and Input Additional Dependencies (opencv_world320d.lib).
Run the executable with the arguments 5 (brush size), 20 (colour intensity), filename.format (including file format)
Output:
gprof Output:
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 79.79 20.17 20.17 1 20.17 24.77 paint(cv::Mat&, cv::Mat&, int, int, int, int) 12.53 23.34 3.17 1742140400 0.00 0.00 cv::Vec<unsigned char, 3>& cv::Mat::at<cv::Vec<unsigned char, 3> >(int, int) 5.62 24.76 1.42 1737354300 0.00 0.00 cv::Vec<unsigned char, 3>::operator[](int) 1.94 25.25 0.49 1 0.49 0.49 cv::Size_<int>::Size_(int, int) ... (there are a lot of other calls to the library that did not significantly affect the profiling)
vs Performance profiler Output:
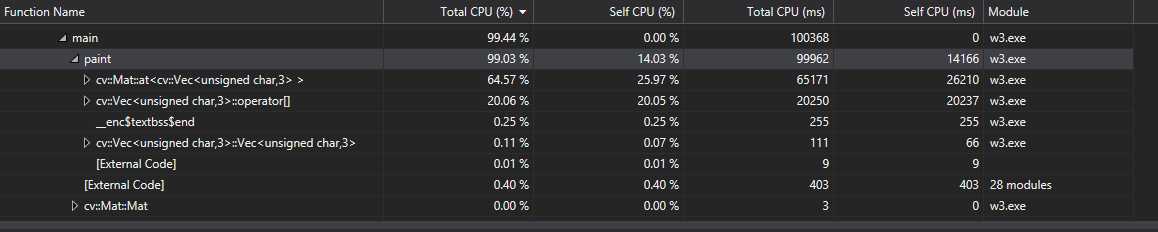
The time required for the program depends largely on the file size being converted. Around 5 seconds for a 50KB image and 100 seconds for a 1MB image. It depends on the brush size and intensity levels as well.
Analysis
The profiling revealed that 80-99% of the processing time is spent in the paint function where the for-loop logic is located. Within that 99% the program spends roughly 2/3 of its time reading accessing data through the "at" function of the OpenCV Mat class (n-dimensional dense array class). The other 1/3 is spent on direct access through OpenCV’s Vec class (short numerical vectors). The for-loop is structured divides the picture up based on brush size. Then it finds the colour for each pixel in that section. Finally, it then averages the intensity to produce the final colour of that group of pixels. This is what makes this program ideal for parallelizing, because each iteration of this for-loop is calculating the final colours for each pixel. (SIMD type of process, the single instruction is to find the final colour and the multiple data is the pixels.)
//Simplified for-loop structure
for (int y = BrushSize; y < (height - BrushSize); y++) //for each row based on brush size
{
for (int x = BrushSize; x < (width - BrushSize); x++) //for each column in brush size
{
for (int j = -BrushSize; j <= BrushSize; j++) //for each pixel row in one brush size grouping
{
for (int i = -BrushSize; i <= BrushSize; i++)//for each pixel column in one brush size grouping
{ //algorithm and logic for colour calculations }
}
}
}
DNA Edit Distance and Sequence Alignment Tool - Analysis by Jonathan D.
This program is a bioinformatics tool which will calculate the edit distance between two sequences. Furthermore, if the option is selected, then the program will also perform a sequence alignment on the two sequences. The two sequences must be given in FASTA format, but there are already ready to use sequences within the test directory of the project.
Original source code can be be found here.
Compilation
To compile the program, navigate to the project’s src directory and run the following command:
$ g++ -std=c++11 -g -pg -O2 BasicEditDistance.cpp main.cpp Parser.cpp Result.cpp Sequence.cpp Solver.cpp SubmatrixCalculator.cpp Writer.cpp
Running the Program
There are three options to run the program, as noted in the github readme:
b - basic edit distance (Needleman-Wunsch)
d - edit distance (Masek-Paterson)
a - edit distance and alignment (Masek-Paterson)
Testing of the program was done by using the "a" option which utilizes the Masek-Paterson algorithm to calculate edit distance and perform alignment sequencing on maximum sequence length of 100 nucleotides. (FASTA files were included in the project under the test directory)
INPUT FILE (test-100.fa):
>Chromosome_3565586_3565685_0:0:0_0:0:0_0/1 ACCGGTTGCCCGCTACATGCTCCAACCATCCGGCGATGGTTACCTGCTGCCGGACTGGTATAGCGCAGAGCCGCGTCGACACCGCGTATCCGTGCCCCCC >Chromosome_3568561_3568661_0:0:1_0:0:1_1/1 TGGGGATTGCCAGTCCGTCCGGGGAGGTATTCAGAAAGGTACACCGGTCTGTTGATATTCATGTAACAGGTATTAATGATGAAGAAAGGAATGGCAAACA
Run the following command to align the two sequences:
$ ./a.out a ../test/data/test-100.fa test.maf
SCREEN OUTPUT:
Submatrix dimension: 1
String A size: 100
String B size: 100
Submatrices in edit table: 100x100
Allocating 230 locations.
Allocation time: 1e-05s
1 / 5 (submatrices: 45 )
5 / 5 (submatrices: 225 )
Submatrix calculation time: 8.9e-05s
Edit path calculation (Masek-Paterson): 0.000149
</h4>TEXT OUTPUT (test.maf)</h4>
a score=58
s Chromosome_3565586_3565685_0:0:0_0:0:0_0/1 0 100 + 107 ACCGG-TTGCCCGCTACATGC-TCCAACCATCCGGCGATGGT-TACCTG-CTGCCG-GACTGGTATAGC--GCAGAGCCGCGTCGACACCGCGTATCCGTGCCCCCC
s Chromosome_3568561_3568661_0:0:1_0:0:1_1/1 0 100 + 107 TGGGGATTGCCAG-TCCGTCCGGGGAGGTATTCAG-AAAGGTACACCGGTCTGTTGATATTCATGTAACAGGTATTAATG-ATGAAGAAAG-GAAT--G-GCAAACA
As you can see, the two sequences are now aligned which will show conserved regions of nucleotides between the two.
Analysis
In order to perform gprof analysis, sequence length of 10000 was used:
$ ./a.out a ../test/data/test-10000.fa test.maf $ gprof -p -b > FULL_O2.analysis.10000.flt
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 36.59 0.45 0.45 302086997 0.00 0.00 std::vector<int, std::allocator<int> >::operator[](unsigned long) 22.77 0.73 0.28 1 0.28 1.05 Solver::fill_edit_matrix() 13.82 0.90 0.17 201301730 0.00 0.00 std::vector<std::vector<int, std::allocator<int> >, std::allocator<std::vector<int, std::allocator<int> > > >::operator[](unsigned long) 12.20 1.05 0.15 25000000 0.00 0.00 SubmatrixCalculator::sumSteps(int) 7.32 1.14 0.09 727566 0.00 0.00 std::vector<int, std::allocator<int> >::size() const 3.25 1.18 0.04 5 0.01 0.01 std::vector<std::vector<int, std::allocator<int> >, std::allocator<std::vector<int, std::allocator<int> > > >::vector() 0.81 1.19 0.01 284812 0.00 0.00 std::_Vector_base<int, std::allocator<int> >::_M_deallocate(int*, unsigned long)
Even with a low sequence length of 10000, we can already begin to see that a lot of time is used in the function call Solver::fill_edit_matrix().
If we run the program for a larger sequence of 50000, the following flat profile is generated.
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls s/call s/call name 85.67 5.61 5.61 1 5.61 5.61 Solver::fill_edit_matrix() 8.09 6.14 0.53 5267025 0.00 0.00 SubmatrixCalculator::calculateFinalSteps(std::__cxx11::basic_string<char, std::char_traits<char>, std::allocator<char> >, std::__cxx11::basic_string<char, std::char_traits<char>, std::allocator<char> >, std::__cxx11::basic_string<char, std::char_traits<char>, std::allocator<char> >, std::__cxx11::basic_string<char, std::char_traits<char>, std::allocator<char> >) 3.05 6.34 0.20 63261681 0.00 0.00 std::vector<std::vector<int, std::allocator<int> >, std::allocator<std::vector<int, std::allocator<int> > > >::_M_fill_insert(__gnu_cxx::__normal_iterator<std::vector<int, std::allocator<int> >*, std::vector<std::vector<int, std::allocator<int> >, std::allocator<std::vector<int, std::allocator<int> > > > >, unsigned long, std::vector<int, std::allocator<int> > const&) 3.05 6.54 0.20 1 0.20 0.93 SubmatrixCalculator::calculate()
At 50000 nucleotides, it is even more clear that the Solver::fill_edit_matrix() function is the dominating term of the execution since it's taking up 85% of the elapsed time.
Below is a snippet of the code:
/*
Backtracks through the submatrices until it reaches the
starting cell. Edit operations in the vector will be ordered backwards
and the integers represent:
1 - moving down in the submatrix
2 - moving right in the submatrix
3 - moving diagonally in the submatrix
*/
void Solver::fill_edit_matrix() {
all_columns.resize(row_num + 1, vector<int>(column_num + 1, 0));
all_rows.resize(row_num + 1, vector<int>(column_num + 1, 0));
top_left_costs.resize(row_num + 1, vector<int>(column_num + 1, 0));
int initialVector = 0;
for (int i = 0; i < submatrix_dim; i++){
initialVector = initialVector * 10 + 2; // 222 == "222" == (1, 1, 1)
}
// padding string b step vectors
for (int submatrix_j = 1; submatrix_j <= column_num; submatrix_j++) {
if ((submatrix_j * submatrix_dim - 1) >= string_b_real_size) {
vector<int> temp_vec(submatrix_dim, 0);
for (int i = 0;
i < (string_b_real_size - ((submatrix_j - 1) * submatrix_dim));
i++)
temp_vec[i] = 1;
all_rows[0][submatrix_j] = SubmatrixCalculator::stepsToInt(temp_vec);
} else {
all_rows[0][submatrix_j] = initialVector;
}
}
// padding string a step vectors
for (int submatrix_i = 1; submatrix_i <= row_num; submatrix_i++) {
if ((submatrix_i * submatrix_dim - 1) >= string_a_real_size) {
vector<int> temp_vec(submatrix_dim, 0);
for (int i = 0;
i < (string_a_real_size - ((submatrix_i - 1) * submatrix_dim));
i++)
temp_vec[i] = 1;
all_columns[submatrix_i][0] =
SubmatrixCalculator::stepsToInt(temp_vec);
} else {
all_columns[submatrix_i][0] = initialVector;
}
}
for (int submatrix_i = 1; submatrix_i <= row_num; submatrix_i++) {
if ((submatrix_i - 1) * submatrix_dim > string_a_real_size)
top_left_costs[submatrix_i][1] = string_a_real_size;
else
top_left_costs[submatrix_i][1] = (submatrix_i - 1) * submatrix_dim;
for (int submatrix_j = 1; submatrix_j <= column_num; submatrix_j++) {
pair<int, int> final_steps = subm_calc->resultIndex[
// offset calculation
str_a_offsets[submatrix_i] + // left string
str_b_offsets[submatrix_j] + // top string
// left steps
subm_calc->stepOffsets[0][all_columns[submatrix_i][submatrix_j - 1]] +
// top steps
subm_calc->stepOffsets[1][all_rows[submatrix_i - 1][submatrix_j]]
];
all_columns[submatrix_i][submatrix_j] = final_steps.first;
all_rows[submatrix_i][submatrix_j] = final_steps.second;
if (submatrix_j != 1) {
top_left_costs[submatrix_i][submatrix_j] =
top_left_costs[submatrix_i][submatrix_j - 1];
top_left_costs[submatrix_i][submatrix_j] += subm_calc->sumSteps(
all_rows[submatrix_i - 1][submatrix_j - 1]);
}
}
}
}
Within the function itself there are many nested loops with calls to the sumSteps function in the SubmatrixCalculator.cpp file. Since the purpose of this function is to retrieve the path through the matrix while calculating the number of steps, this simple operation could benefit from the usage of a GPU rather than a CPU.

