DPS915/CodeCookers

GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary

Project Name Goes here

Team Members

1. Wesley Hamilton, Team leader
2. Norbert Curiciac, Team member
3. Rene Leon Anderson, Team member

Progress

Assignment 1

Norbert: Calculation of PI

Problem Description

For this assignment, I selected one application that I wished to parallelize. I profiled it to find the hotspot of the application and determine if it was feasible to speed up using the GPU.

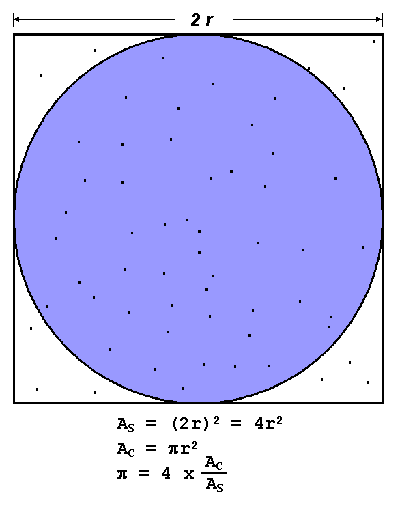
My application that I selected is a PI approximation function. PI can be approximated in a number of ways however I chose to use the dartboard algorithm. Although not the fastest, the algorithm is very feasible to parallelize. The main idea behind it can be compared to a dartboard – you throw a random number (n) of darts at the board and note down the darts that have landed within it and those that have not. The image below demonstrates this concept:

The ratio of the randomly thrown dart is: (hits within dartboard) vs. (hits within square) is equal to the ratio between the two areas i.e. PI/4. The more darts we throw, the better we can approximate PI.

Based on the Blaise Barney's pseudo code (shown above), I created an application which simulates the dart throwing n number of times, providing the approximate value of PI.

Program execution

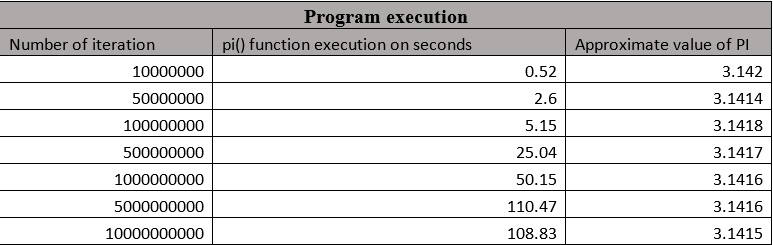
During the execution, the program takes the number of iterations through the command line. It generates two random decimal numbers between 0 and 1 and determines if the randomly generated coordinates are inside in the circle. Then it calculates the size of PI. As we increase the number of iteration we are getting a more realistic value of PI.

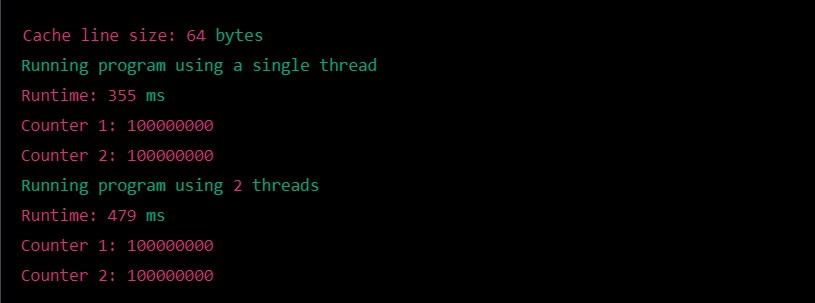
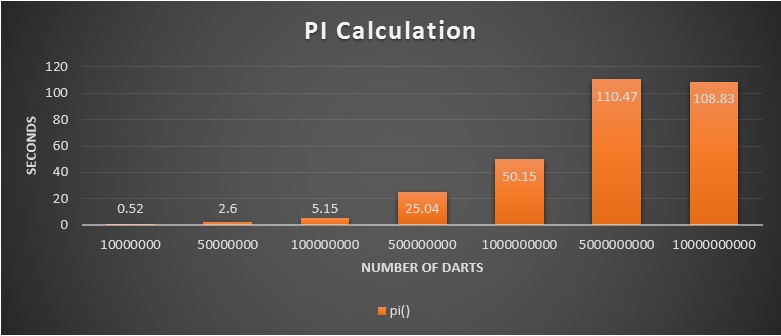
I created a screenshot from the first execution, the rest of the execution is summarized on the table and the chart below.

As we can see the hotspot of the program is the pi () function, which takes 100% of the execution time. This function is containing a single for loop, which is calculating the size of the PI. This can be executed independently, because it has no data dependency, therefor it is possible to parallelize with CUDA to speed up the processing time.

Conclusion

In the above assignment, I described the dartboard algorithm to calculate the size of the PI. I explained and demonstrated the application which I created based on this algorithm. Finally I located the hotspot of the application and defined that it feasible to speed up using GPU.

References:

https://computing.llnl.gov/tutorials/parallel_comp/#ExamplesPI

http://www.mesham.com/article/Dartboard_PI

---

Wesley Hamilton's findings with Prime numbers

For assignment 1, I chose to work on a basic useful algorithm to check to see if there was the possibility to parallelize it. The algorithm takes in a numerical argument and from this number, calculates all the prime numbers from 2 to that number (since 0 and 1 are not prime). Unfortunately for whatever reason gprof could not profile it but I was able to use chrono to test run times.

When the target number is less than a million, the program runs in under a second. Every million items after that though took one more cumulative second then the previous. 1M = 1.104212 secs, 2M = 2.912168 secs, 3M = 5.026149 secs, 4M = 7.468770 secs, and 5M = 10.654563 secs. As you can see, while this is fairly efficient, the program could still use some help spreading the load around.

This seems like a pretty good candidate for a program to be parallelized as It calculates tons of numbers sequentially when ideally it could just do a bunch of them at a time sequentially.

---

Overall Decision

With the above two possible programs to parallelize, our team came to the decision to go with the estimation of Pi as our group project. We came to this decision because while generating prime numbers would be good, the Pi approximation function serves more purposes and would more likely show more interesting results when parallelized with the GPU.