Difference between revisions of "K2"
(→Assignment2) |
(→Assignment2) |
||
| Line 138: | Line 138: | ||
N is 65536, 2^16. | N is 65536, 2^16. | ||
The red box shows Bitonic using GPU, the blue box shows quick using CPU, green box shows bitonic using CPU. | The red box shows Bitonic using GPU, the blue box shows quick using CPU, green box shows bitonic using CPU. | ||
| − | [[File: | + | [[File:16.jpg|500px|thumb|left]] |
| Line 144: | Line 144: | ||
N is 1048576, 2^20. | N is 1048576, 2^20. | ||
| − | [[File: | + | [[File:20.jpg|500px|thumb|left]] |
| Line 150: | Line 150: | ||
N is 16777216, 2^24 | N is 16777216, 2^24 | ||
| − | [[File: | + | [[File:24.jpg|500px|thumb|left]] |
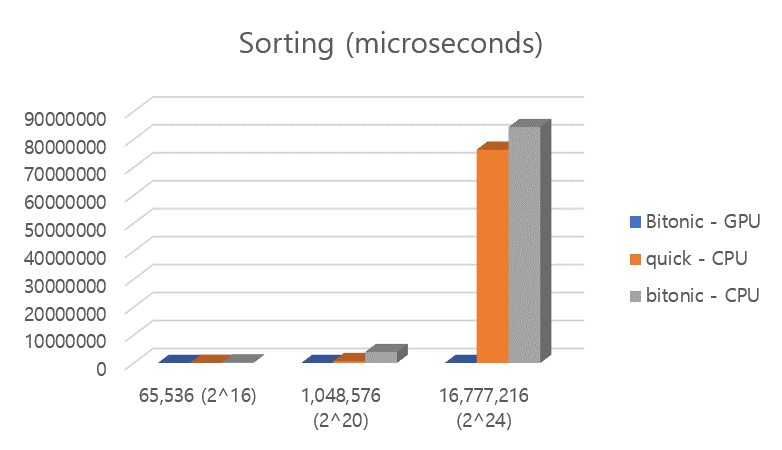
Below is the comparison between bitonic sort using GPU, quick sort using CPU, bitonic sort using CPU. | Below is the comparison between bitonic sort using GPU, quick sort using CPU, bitonic sort using CPU. | ||
[[File:BitonicGraph.jpg]] | [[File:BitonicGraph.jpg]] | ||
Revision as of 23:53, 15 April 2018
Team members
Assignment1
What is Bitonic sorting algorithm?
Bitonic mergesort is a parallel algorithm for sorting. It is also used as a construction method for building a sorting network. The algorithm was devised by Ken Batcher. The resulting sorting networks consist of O( n log^2( n )) comparators and have a delay of O( log^2( n )) , where n is the number of items to be sorted.(https://en.wikipedia.org/wiki/Bitonic_sorter)
(https://www.geeksforgeeks.org/bitonic-sort/)
Analysis and Profiling
The bitonic sorting algorithm is devised for the input length n being a power of 2. To check the noticeable time gap, we put 2^15, 2^20, 2^25.
void bitonicSort(int* array, int N){
int i,j,k;
for (k=2;k<=N;k=2*k) {
for (j=k>>1;j>0;j=j>>1) {
for (i=0;i<N;i++) {
int ixj=i^j;
if ((ixj)>i) {
if ((i&k)==0 && array[i]>array[ixj]){
int temp=array[i];
array[i]=array[ixj];
array[ixj]=temp;
}
if ((i&k)!=0 && array[i]<array[ixj]){
int temp=array[i];
array[i]=array[ixj];
array[ixj]=temp;
}
}
}
}
}
}Flat profile
The size of array:2^16(65536)
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls ms/call ms/call name
100.00 0.07 0.07 1 70.00 70.00 bitonicSort(int*, int)
0.00 0.07 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z11bitonicSortPii
0.00 0.07 0.00 1 0.00 0.00 generateRandom(int*, int)
0.00 0.07 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)The size of array:2^20(1048576)
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
98.94 1.87 1.87 1 1.87 1.87 bitonicSort(int*, int)
1.06 1.89 0.02 1 0.02 0.02 generateRandom(int*, int)
0.00 1.89 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z11bitonicSortPii
0.00 1.89 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)The size of array:2^24(16777216)
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
99.53 41.98 41.98 1 41.98 41.98 bitonicSort(int*, int)
0.47 42.18 0.20 1 0.20 0.20 generateRandom(int*, int)
0.00 42.18 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z11bitonicSortPii
0.00 42.18 0.00 1 0.00 0.00 __static_initialization_and_destruction_0(int, int)Assignment2
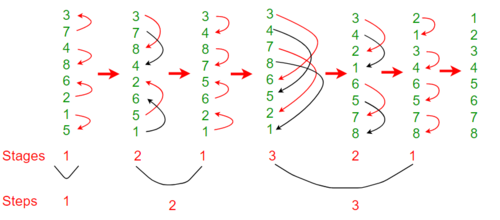
Let's see how this algorithm works to sort.
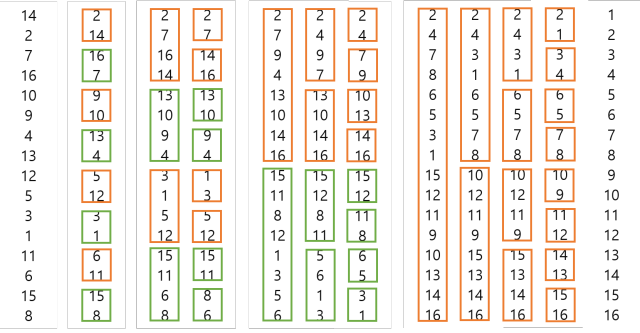
First, array is unsorted array.Second box is stage 1, and the orange boxes are sorted in ascending order and green boxes are sorted in descending order. Third box is stage 2 and it has 2 rounds. In first round, there are 2 orange and green boxes that contains 4 elements. In this case, index 0 and 2 and 1 and 3 will be compared and sorted in ascending if orange box and in descending if green box. Then in round 2, index 0 and 1 , 2 and 3 ... will be compared and sorted. The third and fourth boxes are same.
This is launch statement.
We use nested for loop. i is stage and it increases until log2(n). For example, let say n is 16, so i is 1 to 4. Another for loop represents round and round cannot be bigger than stage.
![]()
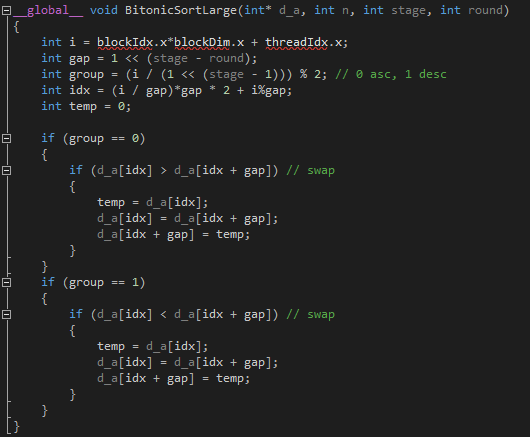
This is bitonic kernel. There are several variables.
Gap expresses gap between 2 elements that will be compared. For example, if stage is 2 and round is 1, gap will be 2. because index 0 will be compared with index 2 and index 1 will be compared with index 3. if stage is 2 and round is 2, gap will be 1 and index 0 will be compared with index 1 so on.
Group shows where each threads are involved in whether ascending or descending order. for example, thread 0 in stage 1 will be 0 because (0 / ( 1 << (1-1))) % 2 = 0 and thread 1 will be 1 because (1 / (1 << (1-1))) % 2 = 1. so in stage 1, thread will have 0 1 0 1 0 1 .... so each threads will sort in ascending and in descending in order. if stage is 2, thread 0 will be 0 and thread 1 will also be 0 because ( 1 / (1 << 1)) % 2 = 0. so each threads in stage 2 will have 0 0 1 1 0 0 1 1 ....
idx shows which elements in array will be picked by threads. For example, thread 0 in stage 1 will have (0 / 1) * 1 * 2 + 0 % 1 = 0, and thread 1 will have (1 / 1) * 1 * 2 + 1 % 1 = 2, and thread 2 will have (2 / 1) * 1 * 2 + 2 % 1 = 4 ... 6, 8, 10. because in stage 1, index 0 will be compared with 1, 2 compared with 3, 4 compared with 5 .... another example, if thread 0 in round 1 in stage 2 will have ( 0 / 2)*2*2 + 0%2 = 0, thread 1 will have ( 1/2)*2*2 + 1%2 = 1, thread 2 will have ( 2/2)*2*2 + 2%2 = 4, thread 3 will have (3/2) * 2 * 2 + 3%2 = 5. So threads will have 0, 1, 4, 5, 8, 9 .... because in round 1 in stage 2, index 0 will be compared with 2 and 1 compared with 3, 4 compared with 6 and 5 compared with 7.
N is 65536, 2^16. The red box shows Bitonic using GPU, the blue box shows quick using CPU, green box shows bitonic using CPU.
N is 1048576, 2^20.
N is 16777216, 2^24
Below is the comparison between bitonic sort using GPU, quick sort using CPU, bitonic sort using CPU.