Difference between revisions of "GPU610 Team Tsubame"
Yanhao Lei (talk | contribs) (→Assignment 1) |
Yanhao Lei (talk | contribs) (→Pi) |
||
| Line 14: | Line 14: | ||
* '''System Specifications''' | * '''System Specifications''' | ||
| − | OS: Windows 7 (64-bit) | + | OS: Windows 7 (64-bit) |
| − | CPU: Intel Core i3-2350M @ 2.30GHz | + | CPU: Intel Core i3-2350M @ 2.30GHz |
| − | GPU: GeForce GT 520MX (48 CUDA cores) | + | GPU: GeForce GT 520MX (48 CUDA cores) |
* '''How To Execute On Linux?''' | * '''How To Execute On Linux?''' | ||
| Line 88: | Line 88: | ||
* '''Stage 2 - Potential Speedup | * '''Stage 2 - Potential Speedup | ||
Using Amdahl's Law: | Using Amdahl's Law: | ||
| − | P = 1708ms /1725ms (using the third test data from below...) | + | P = 1708ms / 1725ms (using the third test data from below...) |
P = 0.99014 | P = 0.99014 | ||
n = 48 (processors reported by deviceQuery.exe) | n = 48 (processors reported by deviceQuery.exe) | ||
| − | Sn = 1 / ( 1 - P + P/n ) | + | Sn = 1 / ( 1 - P + P / n ) |
S48 = 1 / ( 1 - 0.99014 + 0.99014 / 48 ) | S48 = 1 / ( 1 - 0.99014 + 0.99014 / 48 ) | ||
S48 = 32.79988 | S48 = 32.79988 | ||
| Line 186: | Line 186: | ||
* '''Stage 1 - Big-O:''' | * '''Stage 1 - Big-O:''' | ||
| − | The (predicted) hotspot begins from line 35 and ends at line 44. Although there are two for loops, the outer for loop executes ''n'' / ''stride'' times while the inner for loop executes ''stride'' times; the actual iteration is just ''n''. | + | The (predicted) hotspot begins from line 35 and ends at line 44. Although there are two for loops, the outer for loop executes ''n'' / ''stride'' times while the inner for loop executes ''stride'' times; the actual iteration is just ''n'' ( O(n) ). |
* '''Stage 2 - Potential Speedup:''' | * '''Stage 2 - Potential Speedup:''' | ||
Using Amdahl's Law: | Using Amdahl's Law: | ||
| − | P = | + | P = 10883ms / 10903ms (using the last sample of the third test data from below...) |
| − | P = 0. | + | P = 0.99817 |
n = 48 (processors reported by deviceQuery.exe) | n = 48 (processors reported by deviceQuery.exe) | ||
| − | Sn = 1 / ( 1 - P + P/n ) | + | Sn = 1 / ( 1 - P + P / n ) |
| − | S48 = 1 / ( 1 - 0. | + | S48 = 1 / ( 1 - 0.99817 + 0.99817 / 48 ) |
| − | S48 = | + | S48 = 44.19015 |
| − | The maximum speedup on the test system is approximately | + | The maximum speedup on the test system is approximately 44 times. |
At around 10K iterations, the first decimal is stable. | At around 10K iterations, the first decimal is stable. | ||
Revision as of 22:08, 9 February 2017
Contents
TBD...
Team Member
- Mark Anthony Villaflor (Leader)
- Huachen Li
- Yanhao Lei
eMail All
Progress
Assignment 1
Pi
This is a comparison between two programs that calculate Pi.
- System Specifications
OS: Windows 7 (64-bit) CPU: Intel Core i3-2350M @ 2.30GHz GPU: GeForce GT 520MX (48 CUDA cores)
- How To Execute On Linux?
1. Here is the Makefile:
# Change this to "monte-carlo" if needed
VER = leibniz
# Uncomment and modify the following lines to specify a specific version of GCC
#GCC_VERSION = 5.2.0
#PREFIX = /usr/local/gcc/${GCC_VERSION}/bin/
CC = ${PREFIX}gcc
CPP = ${PREFIX}g++
$(VER): $(VER).o ; \
$(CPP) -g -pg -o$(VER) $(VER).o
$(VER).o: $(VER).cpp ; \
$(CPP) -c -O2 -g -pg -std=c++14 $(VER).cpp
# Remember to ">make clean" after ">make" to cleanup if the cleaning does not happen automatically
clean: ; \
rm *\.o
2. Download leibniz.cpp and monte-carlo.cpp and put them into the same directory as the Makefile.
3. Execute the following command (in the same directory as the Makefile):
> make
Leibniz formula implementation:
01 #include <iostream> 02 #include <iomanip> 03 04 #include <chrono> 05 06 // Function duplicated from Workshop 2 - BLAS 07 void reportTime(const char* msg, std::chrono::steady_clock::duration span) { 08 auto ms = std::chrono::duration_cast<std::chrono::milliseconds>(span); 09 std::cout << msg << " - took - " 10 << ms.count() << " millisecs" << std::endl; 11 } 12 13 // Arctangent of 1; execute for ~n iterations to refine the result 14 long double arctan1( unsigned long long int it ) { 15 long double r = 0.0; // 1 op. (=) runs 1 time 16 17 // v0.25; due to performing the operations in a different order, there are rounding issues... 18 for ( long double d = 0.0; d < it; d++ ) { // 1 op. (=) runs 1 time; 2 op.s (<, ++) run n times 19 long double de = d * 4.0 + 1.0; // 3 op.s (=, *, +) run n times 20 r += (1.0 / de) - (1.0 / (de + 2.0)); // 6 op.s (+ & =, /, -, /, +) run n times 21 } 22 23 return r; // 1 op. (return) runs 1 time 24 } 25 26 int main( int argc, char* argv[] ) { 27 unsigned long long int n = std::stoull(argv[1], 0); 28 29 std::chrono::steady_clock::time_point ts, te; 30 ts = std::chrono::steady_clock::now(); 31 long double pi = 4.0 * arctan1( n ); 32 te = std::chrono::steady_clock::now(); 33 reportTime("Arctangent(1) ", te - ts); 34 35 // Maximum length of a long double is 64 digits; minus "3." gives 62 digits. 36 std::cout.precision(62); 37 std::cout << "Pi: " << std::fixed << pi << std::endl; 40 }
- Stage 1 - Big-O:
There is only one for loop in this program (on line 18); it executes d times, where d is the first argument provided to the program on the command line. Summing up the operations in the (predicted) hotspot, T(n) = 11n + 3; therefore O(n) runtime.
- Stage 2 - Potential Speedup
Using Amdahl's Law:
P = 1708ms / 1725ms (using the third test data from below...) P = 0.99014 n = 48 (processors reported by deviceQuery.exe) Sn = 1 / ( 1 - P + P / n ) S48 = 1 / ( 1 - 0.99014 + 0.99014 / 48 ) S48 = 32.79988
The maximum speedup on the test system is approximately 33 times.
4 digits are correct at 10K iterations:
> time ./leibniz 10000 Arctangent(1) - took - 0 millisecs Pi: 3.14154265358982449354505184224706226814305409789085388183593750 real 0m0.016s user 0m0.004s sys 0m0.008s
7 digits are correct at 10M iterations:
> time ./leibniz 10000000 Arctangent(1) - took - 171 millisecs Pi: 3.14159260358979321929411010483335076060029678046703338623046875 real 0m0.187s user 0m0.172s sys 0m0.012s
No difference at 100M iterations:
> time ./leibniz 100000000 Arctangent(1) - took - 1708 millisecs Pi: 3.14159264858979533105269588144636827564681880176067352294921875 real 0m1.725s user 0m1.704s sys 0m0.008s
Monte-Carlo algorithm implementation:
01 #include <iostream> 02 #include <random> 03 04 #include <chrono> 05 06 // Duplicated from https://scs.senecac.on.ca/~gpu610/pages/workshops/w2.html 07 void reportTime(const char* msg, std::chrono::steady_clock::duration span) { 08 auto ms = std::chrono::duration_cast<std::chrono::milliseconds>(span); 09 std::cout << msg << " - took - " << 10 ms.count() << " millisecs" << std::endl; 11 } 12 13 int main(int argc, char* argv[]) { 14 std::chrono::steady_clock::time_point ts, te; 15 16 ts = std::chrono::steady_clock::now(); 17 unsigned long long int n = std::stoull(argv[1], 0), 18 totalCircle = 0; 19 20 int stride = 1000, 21 circleSize = n / stride; 22 23 unsigned int* circle = new unsigned int[circleSize]; 24 25 for (int i = 0; i < circleSize; i++) 26 circle[i] = 0; 27 28 std::random_device rd; 29 std::mt19937 mt(rd()); 30 std::uniform_real_distribution<long double> dist(0.0, 1.0); 31 te = std::chrono::steady_clock::now(); 32 reportTime("Init. ", te - ts); 33 34 ts = std::chrono::steady_clock::now(); 35 for (unsigned long long int i = 0; i < circleSize; i++) { 36 for (int j = 0; j < stride; j++) { 37 long double x = dist(mt), 38 y = dist(mt); 39 // if position is inside the circle... 40 if (x * x + y * y < 1.0) { 41 circle[i]++; 42 } 43 } 44 } 45 46 for (int i = 0; i < circleSize; i++) 47 totalCircle += circle[i]; 48 49 long double pi = 4.0 * ((long double) totalCircle) / ((long double) n); 50 te = std::chrono::steady_clock::now(); 51 reportTime("Drop points ", te - ts); 52 53 std::cout.precision(62); 54 std::cout << "Pi: " << std::fixed << pi << std::endl; 55 56 delete [] circle; 57 }
- Stage 1 - Big-O:
The (predicted) hotspot begins from line 35 and ends at line 44. Although there are two for loops, the outer for loop executes n / stride times while the inner for loop executes stride times; the actual iteration is just n ( O(n) ).
- Stage 2 - Potential Speedup:
Using Amdahl's Law:
P = 10883ms / 10903ms (using the last sample of the third test data from below...) P = 0.99817 n = 48 (processors reported by deviceQuery.exe) Sn = 1 / ( 1 - P + P / n ) S48 = 1 / ( 1 - 0.99817 + 0.99817 / 48 ) S48 = 44.19015
The maximum speedup on the test system is approximately 44 times.
At around 10K iterations, the first decimal is stable.
> time ./monte-carlo 10000 Init. - took - 0 millisecs Drop points - took - 1 millisecs Pi: 3.11679999999999999995940747066214271399076096713542938232421875 real 0m0.019s user 0m0.004s sys 0m0.008s > time ./monte-carlo 10000 Init. - took - 0 millisecs Drop points - took - 1 millisecs Pi: 3.16480000000000000009124645483638005316606722772121429443359375 real 0m0.018s user 0m0.008s sys 0m0.004s > time ./monte-carlo 10000 Init. - took - 0 millisecs Drop points - took - 1 millisecs Pi: 3.16639999999999999995108079797745403993758372962474822998046875 real 0m0.018s user 0m0.004s sys 0m0.008s
The next digit is stable at around 10M iterations
> time ./monte-carlo 10000000 Init. - took - 0 millisecs Drop points - took - 1096 millisecs Pi: 3.14150879999999999990685506379151092914980836212635040283203125 real 0m1.114s user 0m1.092s sys 0m0.008s > time ./monte-carlo 10000000 Init. - took - 0 millisecs Drop points - took - 1097 millisecs Pi: 3.14219679999999999993332000514101309818215668201446533203125000 real 0m1.114s user 0m1.092s sys 0m0.016s > time ./monte-carlo 10000000 Init. - took - 0 millisecs Drop points - took - 1097 millisecs Pi: 3.14158840000000000010696443730751070688711479306221008300781250 real 0m1.115s user 0m1.088s sys 0m0.012s
By 100M, the third digit appears to be stable.
> time ./monte-carlo 100000000 Init. - took - 1 millisecs Drop points - took - 10910 millisecs Pi: 3.14138611999999999989559296142971334120375104248523712158203125 real 0m10.930s user 0m10.881s sys 0m0.012s > time ./monte-carlo 100000000 Init. - took - 1 millisecs Drop points - took - 10847 millisecs Pi: 3.14185203999999999998835042980260823242133483290672302246093750 real 0m10.868s user 0m10.833s sys 0m0.016s > time ./monte-carlo 100000000 Init. - took - 1 millisecs Drop points - took - 10883 millisecs Pi: 3.14160056000000000009896028441147564080893062055110931396484375 real 0m10.903s user 0m10.865s sys 0m0.016s
Maze
Testing Environment:
- Operating system: Linux
- Compiler: g++ 5.2.0
- Processor: Dual-Core AMD Opteron(tm) Processor 8220
- System memory: 3098088 kB
How to setup:
1. Download source file: https://github.com/corzani/maze
2. Create “Makefile” file:
# Makefile for GPU610/assigment1/maze
#
GCC_VERSION = 5.2.0
PREFIX = /usr/local/gcc/${GCC_VERSION}/bin/
CC = ${PREFIX}gcc
CPP = ${PREFIX}g++
OBJS = Maze.o MazeDebug.o MazePng.o main.o
SOURCE = Maze.cpp MazeDebug.cpp MazePng.cpp main.cpp
LIBS = -lpng
TARGET = maze
$(TARGET): $(OBJS)
$(CPP) -pg -o$(TARGET) $(OBJS) $(LIBS)
$(OBJS): $(SOURCE)
$(CPP) -c -O2 -g -pg -std=c++14 $(SOURCE)
#all: $(TARGET)
clean:
rm *.o
3. Complile and run:
> make > maze <maze x axes> <maze y axes>
Example:
> maze 5000 5000
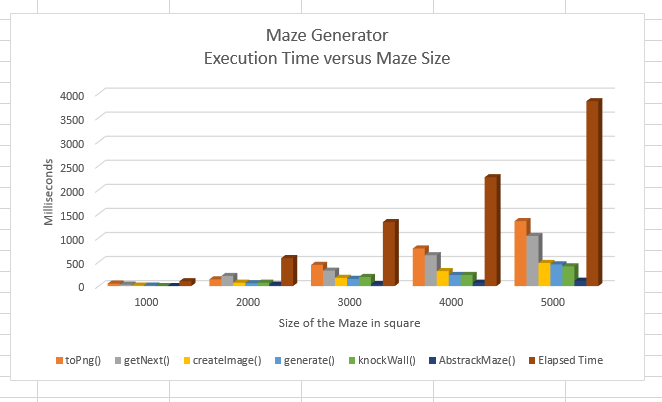
Analysis:
The program function named toPng() takes up an average of 42% (min: 35%; max: 50%) of the execution time. The reason for toPng() to take so much runtime is because of the for loop that building the walls of the maze.
for (int i = 0; i < height; ++i) {
row_pointers[i] = new png_byte[width * 3];
for (int j = 0; j < width * 3; j += 3) {
row_pointers[i][j] = WALL;
row_pointers[i][j + 1] = WALL;
row_pointers[i][j + 2] = WALL;
}
}
The function also has a runtime of O(n^2).
For n = 1000
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls ms/call ms/call name 50.00 0.05 0.05 MazePng::toPng(unsigned int) 30.00 0.08 0.03 1999978 0.00 0.00 AbstractMaze::getNext(unsigned int, short*, unsigned int*) 10.00 0.09 0.01 1 10.00 10.00 MazePng::createImage(unsigned char**, unsigned int) 10.00 0.10 0.01 AbstractMaze::generate(int) 0.00 0.10 0.00 999999 0.00 0.00 AbstractMaze::knockWall(unsigned int, unsigned int, AbstractMaze::directions) 0.00 0.10 0.00 7798 0.00 0.00 _ZNSt5dequeIjSaIjEE16_M_push_back_auxIJjEEEvDpOT_ 0.00 0.10 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::_M_initialize_map(unsigned int) 0.00 0.10 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::~_Deque_base() 0.00 0.10 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN12AbstractMaze3mapE 0.00 0.10 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN7MazePngC2Ejj 0.00 0.10 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN9MazeDebugC2Ejj 0.00 0.10 0.00 1 0.00 0.00 _GLOBAL__sub_I_main 0.00 0.10 0.00 1 0.00 0.00 AbstractMaze::AbstractMaze(unsigned int, unsigned int)
For n = 2000
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls ms/call ms/call name 36.21 0.21 0.21 7999992 0.00 0.00 AbstractMaze::getNext(unsigned int, short*, unsigned int*) 24.14 0.35 0.14 MazePng::toPng(unsigned int) 12.07 0.42 0.07 3999999 0.00 0.00 AbstractMaze::knockWall(unsigned int, unsigned int, AbstractMaze::directions) 12.07 0.49 0.07 1 70.00 70.00 MazePng::createImage(unsigned char**, unsigned int) 10.34 0.55 0.06 AbstractMaze::generate(int) 5.17 0.58 0.03 1 30.00 30.00 AbstractMaze::AbstractMaze(unsigned int, unsigned int) 0.00 0.58 0.00 31113 0.00 0.00 _ZNSt5dequeIjSaIjEE16_M_push_back_auxIJjEEEvDpOT_ 0.00 0.58 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::_M_initialize_map(unsigned int) 0.00 0.58 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::~_Deque_base() 0.00 0.58 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN12AbstractMaze3mapE 0.00 0.58 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN7MazePngC2Ejj 0.00 0.58 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN9MazeDebugC2Ejj 0.00 0.58 0.00 1 0.00 0.00 _GLOBAL__sub_I_main
For n = 3000
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls ms/call ms/call name 33.08 0.44 0.44 MazePng::toPng(unsigned int) 24.06 0.76 0.32 17999970 0.00 0.00 AbstractMaze::getNext(unsigned int, short*, unsigned int*) 14.29 0.95 0.19 8999999 0.00 0.00 AbstractMaze::knockWall(unsigned int, unsigned int, AbstractMaze::directions) 12.78 1.12 0.17 1 170.00 170.00 MazePng::createImage(unsigned char**, unsigned int) 11.28 1.27 0.15 AbstractMaze::generate(int) 3.01 1.31 0.04 1 40.00 40.00 AbstractMaze::AbstractMaze(unsigned int, unsigned int) 1.50 1.33 0.02 70076 0.00 0.00 _ZNSt5dequeIjSaIjEE16_M_push_back_auxIJjEEEvDpOT_ 0.00 1.33 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::_M_initialize_map(unsigned int) 0.00 1.33 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::~_Deque_base() 0.00 1.33 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN12AbstractMaze3mapE 0.00 1.33 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN7MazePngC2Ejj 0.00 1.33 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN9MazeDebugC2Ejj 0.00 1.33 0.00 1 0.00 0.00 _GLOBAL__sub_I_main
For n = 4000
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls ms/call ms/call name 34.51 0.78 0.78 MazePng::toPng(unsigned int) 28.32 1.42 0.64 31999957 0.00 0.00 AbstractMaze::getNext(unsigned int, short*, unsigned int*) 13.72 1.73 0.31 1 310.00 310.00 MazePng::createImage(unsigned char**, unsigned int) 10.18 1.96 0.23 15999999 0.00 0.00 AbstractMaze::knockWall(unsigned int, unsigned int, AbstractMaze::directions) 10.18 2.19 0.23 AbstractMaze::generate(int) 3.10 2.26 0.07 1 70.00 70.00 AbstractMaze::AbstractMaze(unsigned int, unsigned int) 0.00 2.26 0.00 124808 0.00 0.00 _ZNSt5dequeIjSaIjEE16_M_push_back_auxIJjEEEvDpOT_ 0.00 2.26 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::_M_initialize_map(unsigned int) 0.00 2.26 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::~_Deque_base() 0.00 2.26 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN12AbstractMaze3mapE 0.00 2.26 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN7MazePngC2Ejj 0.00 2.26 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN9MazeDebugC2Ejj 0.00 2.26 0.00 1 0.00 0.00 _GLOBAL__sub_I_main
For n = 5000
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls ms/call ms/call name 35.16 1.35 1.35 MazePng::toPng(unsigned int) 27.08 2.39 1.04 49999831 0.00 0.00 AbstractMaze::getNext(unsigned int, short*, unsigned int*) 12.50 2.87 0.48 1 480.00 480.00 MazePng::createImage(unsigned char**, unsigned int) 11.72 3.32 0.45 AbstractMaze::generate(int) 10.68 3.73 0.41 24999999 0.00 0.00 AbstractMaze::knockWall(unsigned int, unsigned int, AbstractMaze::directions) 2.86 3.84 0.11 1 110.00 110.00 AbstractMaze::AbstractMaze(unsigned int, unsigned int) 0.00 3.84 0.00 195749 0.00 0.00 _ZNSt5dequeIjSaIjEE16_M_push_back_auxIJjEEEvDpOT_ 0.00 3.84 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::_M_initialize_map(unsigned int) 0.00 3.84 0.00 2 0.00 0.00 std::_Deque_base<unsigned int, std::allocator<unsigned int> >::~_Deque_base() 0.00 3.84 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN12AbstractMaze3mapE 0.00 3.84 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN7MazePngC2Ejj 0.00 3.84 0.00 1 0.00 0.00 _GLOBAL__sub_I__ZN9MazeDebugC2Ejj 0.00 3.84 0.00 1 0.00 0.00 _GLOBAL__sub_I_main
Summary:
Function toPng() has an average of 42% execution time. It also has O(n^2) runtime.