Difference between revisions of "Team Name (Official)"
(→Topic) |
(→Assignment 3) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{GPU610/DPS915 Index | 20131}} | {{GPU610/DPS915 Index | 20131}} | ||
[[Image:teamname.png|right|frameless|widthpx| ]] | [[Image:teamname.png|right|frameless|widthpx| ]] | ||
| − | = | + | = Optimus Prime = |
| + | |||
| + | |||
| + | |||
| + | The following page outlines the three-step progression through a program that counts the number of primes between 1 and N. | ||
| + | |||
| + | |||
== Team Members == | == Team Members == | ||
| − | # [mailto:gtsmyth@learn.senecac.on.ca?subject=gpu610 Graeme Smyth], | + | # [mailto:gtsmyth@learn.senecac.on.ca?subject=gpu610 Graeme Smyth], primary coder |
| − | # [mailto:rhotin@learn.senecac.on.ca?subject=gpu610 Roman Hotin], | + | # [mailto:rhotin@learn.senecac.on.ca?subject=gpu610 Roman Hotin], primary coder |
[mailto:gtsmyth@learn.senecac.on.ca,rhotin@learn.senecac.on.ca?subject=dps901-gpu610 Email All] | [mailto:gtsmyth@learn.senecac.on.ca,rhotin@learn.senecac.on.ca?subject=dps901-gpu610 Email All] | ||
== Progress == | == Progress == | ||
=== Assignment 3 === | === Assignment 3 === | ||
| − | + | A3 was difficult to produce, due to the shear success of A2. Still, some optimizations were found. See below. | |
| + | |||
| + | Please note the preliminary check for division by 2, 3, 5, 7 and 11. By checking these common primes first, we could eliminate most possibilities without even entering a loop. It is very insignificant, but helps in most cases. | ||
| + | |||
| + | <pre> | ||
| + | __global__ void findPrimes(int* answer, int n) | ||
| + | { | ||
| + | int i = threadIdx.x; | ||
| + | int j = blockIdx.x * blockDim.x + threadIdx.x; | ||
| + | __shared__ int blockSum[ntpb]; | ||
| + | |||
| + | int check = j+1; | ||
| + | |||
| + | blockSum[i] = 0; | ||
| + | __syncthreads(); | ||
| + | |||
| + | if(check >= 2 && check <= n) | ||
| + | { | ||
| + | bool flag = true; //Assume prime | ||
| + | |||
| + | if((check % 2 == 0 && check != 2) || | ||
| + | (check % 3 == 0 && check != 3) || | ||
| + | (check % 5 == 0 && check != 5) || | ||
| + | (check % 7 == 0 && check != 7) || | ||
| + | (check % 11 == 0 && check != 11)) //If divisible by x | ||
| + | flag = false; //Found to not be prime | ||
| + | for(int x = 2; x < check/2 && flag; x++) //Check all numbers 2 to "check" | ||
| + | if(check % x == 0) //If divisible by x | ||
| + | flag = false; //Found to not be prime | ||
| + | |||
| + | if(flag) //If prime | ||
| + | blockSum[i] = 1; //Add one to our numbers | ||
| + | } | ||
| + | |||
| + | __syncthreads(); //Ensure all threads are caught up | ||
| + | |||
| + | for (int stride = blockDim.x >> 1; stride > 0; stride >>= 1) | ||
| + | { | ||
| + | if (i < stride) | ||
| + | blockSum[i] += blockSum[i + stride]; | ||
| + | __syncthreads(); | ||
| + | } | ||
| + | |||
| + | if (i == 0) | ||
| + | answer[blockIdx.x] = blockSum[0]; | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | |||
| + | The biggest significance was in the numbers we checked. Note the "check/2" in our for loop, which wasn't divided by 2 in A2. | ||
| + | |||
| + | Consider if 150 is prime: | ||
| + | |||
| + | 150 / 75 = 2 | ||
| + | |||
| + | 150 / 76 = 1.9... | ||
| + | |||
| + | ... | ||
| + | |||
| + | 150 / 150 = 1 | ||
| + | |||
| + | |||
| + | The lowest integer a division can produce that results in a prime is 2. | ||
| + | |||
| + | In other words, the highest number we need check 150 for is 75, as all numbers between 1 and 2 aren't integers, and being 1 (150/150) doesn't make it prime. | ||
| + | |||
| + | Hence, for checking if X is prime, we need only check from 1 to X/2, not to X. | ||
| + | |||
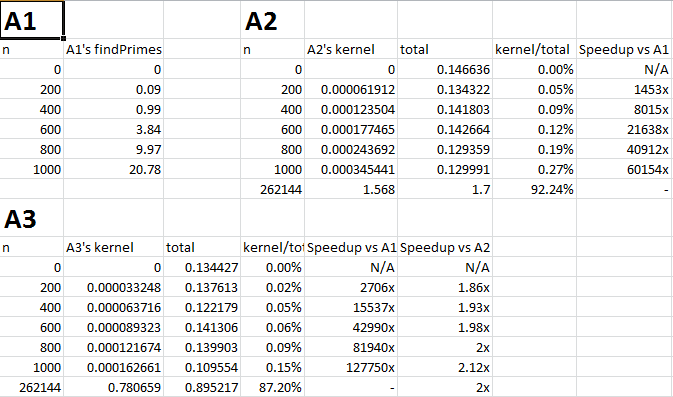
| + | This created a speedup of roughly 2x, as compared to A2. | ||
| + | |||
| + | Compared to A1, the results were more than 125,000x for n=1000. | ||
| + | |||
| + | |||
| + | |||
| + | Higher values of n were not checked, due to the ridiculously long time A1 would take. | ||
| + | |||
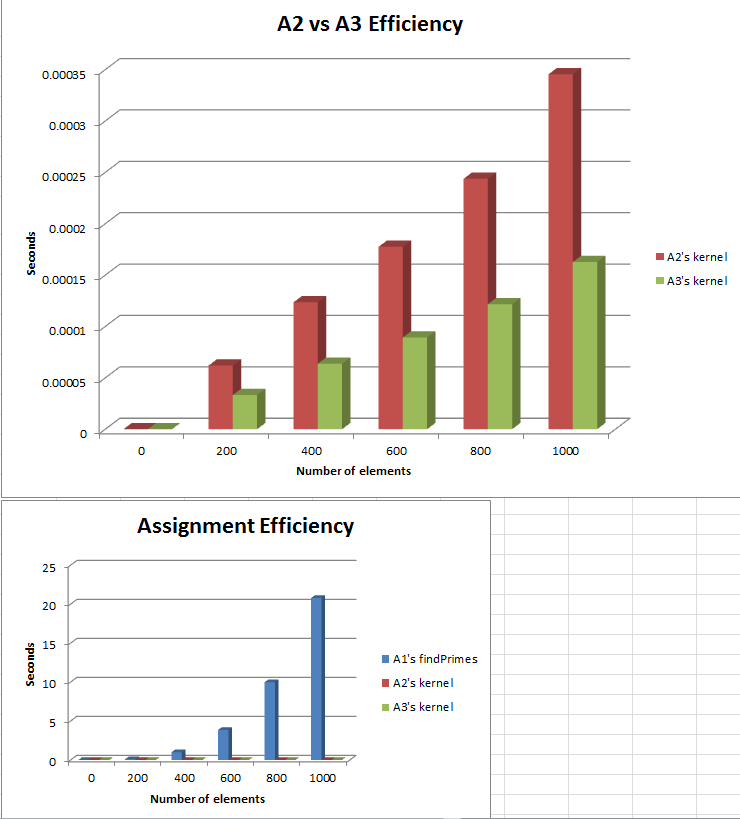
| + | For comparison's sake, A2 and A3 were compared using the max value they could compute (maxThreads * maxBlocks, 512 * 512 = 262,144). Even at such high numbers, A3 is still 2x more efficient than A2. | ||
| + | |||
| + | |||
| + | |||
| + | Other forms of optimization were not possible. | ||
| + | Memory coalescence couldn't be done, as we aren't accessing values within an array (like a vector or matrix). | ||
| + | |||
| + | When checking if a number is divisible by something, you need only check primes (Is it divisible by 2? 3? 5? 7? etc). | ||
| + | You don't need to check non-primes. | ||
| + | |||
| + | We thought we could store all primes found. That way, threads could merely check the previously found primes, instead of all numbers 1 to x/2. However, the logic structure of parallelization doesn't permit this, due to threads running simultaneously. This means that a list of primes wouldn't exist prior to running any of the threads. | ||
| + | |||
| + | |||
| + | This means that the simple algorithm improvements made appear to be the only optimizations possible. | ||
| + | |||
| + | |||
| + | Data for all assignments, with available graphs, is shown below. | ||
| + | |||
| − | |||
| − | + | [[Image:Gtsmyth a3.png|widthpx| ]] | |
| + | [[Image:Gtsmyth a3 2.png|widthpx| ]] | ||
=== Assignment 2 === | === Assignment 2 === | ||
| Line 81: | Line 180: | ||
//DPS915 Assignment 1 | //DPS915 Assignment 1 | ||
// | // | ||
| − | //Graeme Smyth | + | //Graeme Smyth |
//Code written by Graeme Smyth, with inspiration from course Workshop 1 | //Code written by Graeme Smyth, with inspiration from course Workshop 1 | ||
//February 7th, 2013 | //February 7th, 2013 | ||
Latest revision as of 23:05, 11 April 2013
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
Optimus Prime
The following page outlines the three-step progression through a program that counts the number of primes between 1 and N.
Team Members
- Graeme Smyth, primary coder
- Roman Hotin, primary coder
Progress
Assignment 3
A3 was difficult to produce, due to the shear success of A2. Still, some optimizations were found. See below.
Please note the preliminary check for division by 2, 3, 5, 7 and 11. By checking these common primes first, we could eliminate most possibilities without even entering a loop. It is very insignificant, but helps in most cases.
__global__ void findPrimes(int* answer, int n)
{
int i = threadIdx.x;
int j = blockIdx.x * blockDim.x + threadIdx.x;
__shared__ int blockSum[ntpb];
int check = j+1;
blockSum[i] = 0;
__syncthreads();
if(check >= 2 && check <= n)
{
bool flag = true; //Assume prime
if((check % 2 == 0 && check != 2) ||
(check % 3 == 0 && check != 3) ||
(check % 5 == 0 && check != 5) ||
(check % 7 == 0 && check != 7) ||
(check % 11 == 0 && check != 11)) //If divisible by x
flag = false; //Found to not be prime
for(int x = 2; x < check/2 && flag; x++) //Check all numbers 2 to "check"
if(check % x == 0) //If divisible by x
flag = false; //Found to not be prime
if(flag) //If prime
blockSum[i] = 1; //Add one to our numbers
}
__syncthreads(); //Ensure all threads are caught up
for (int stride = blockDim.x >> 1; stride > 0; stride >>= 1)
{
if (i < stride)
blockSum[i] += blockSum[i + stride];
__syncthreads();
}
if (i == 0)
answer[blockIdx.x] = blockSum[0];
}
The biggest significance was in the numbers we checked. Note the "check/2" in our for loop, which wasn't divided by 2 in A2.
Consider if 150 is prime:
150 / 75 = 2
150 / 76 = 1.9...
...
150 / 150 = 1
The lowest integer a division can produce that results in a prime is 2.
In other words, the highest number we need check 150 for is 75, as all numbers between 1 and 2 aren't integers, and being 1 (150/150) doesn't make it prime.
Hence, for checking if X is prime, we need only check from 1 to X/2, not to X.
This created a speedup of roughly 2x, as compared to A2.
Compared to A1, the results were more than 125,000x for n=1000.
Higher values of n were not checked, due to the ridiculously long time A1 would take.
For comparison's sake, A2 and A3 were compared using the max value they could compute (maxThreads * maxBlocks, 512 * 512 = 262,144). Even at such high numbers, A3 is still 2x more efficient than A2.
Other forms of optimization were not possible. Memory coalescence couldn't be done, as we aren't accessing values within an array (like a vector or matrix).
When checking if a number is divisible by something, you need only check primes (Is it divisible by 2? 3? 5? 7? etc). You don't need to check non-primes.
We thought we could store all primes found. That way, threads could merely check the previously found primes, instead of all numbers 1 to x/2. However, the logic structure of parallelization doesn't permit this, due to threads running simultaneously. This means that a list of primes wouldn't exist prior to running any of the threads.
This means that the simple algorithm improvements made appear to be the only optimizations possible.
Data for all assignments, with available graphs, is shown below.
Assignment 2
A2 featured a significantly improved prime-counting algorithm, coupled with GPU integration.
Going from A1 to A2, our code experienced a speed-up of 6,015,300% (or 60,154x faster (literally - A1 was that inefficient)).
Kernel code for A2:
__global__ void findPrimes(int* answer, int n)
{
int i = threadIdx.x;
int j = blockIdx.x * blockDim.x + threadIdx.x;
__shared__ int blockSum[ntpb];
int check = j+1;
blockSum[i] = 0;
__syncthreads();
if(check >= 2 && check <= n)
{
bool flag = true; //Assume prime
for(int x = 2; x < check && flag; x++) //Check all numbers 2 to "check"
if(check % x == 0) //If divisible by x
flag = false; //Found to not be prime
if(flag) //If prime
blockSum[i] = 1; //Add one to our numbers
}
__syncthreads(); //Ensure all threads are caught up
for (int stride = blockDim.x >> 1; stride > 0; stride >>= 1)
{
if (i < stride)
blockSum[i] += blockSum[i + stride];
__syncthreads();
}
if (i == 0)
answer[blockIdx.x] = blockSum[0];
}
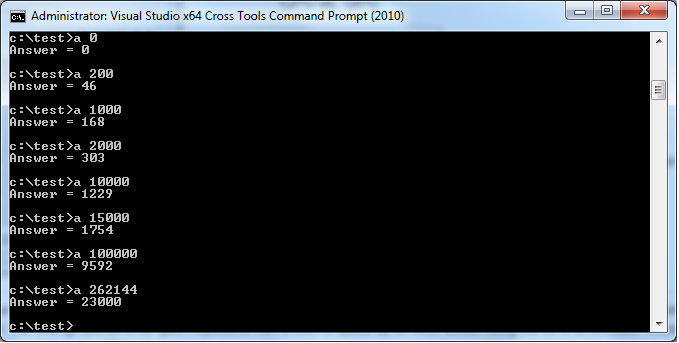
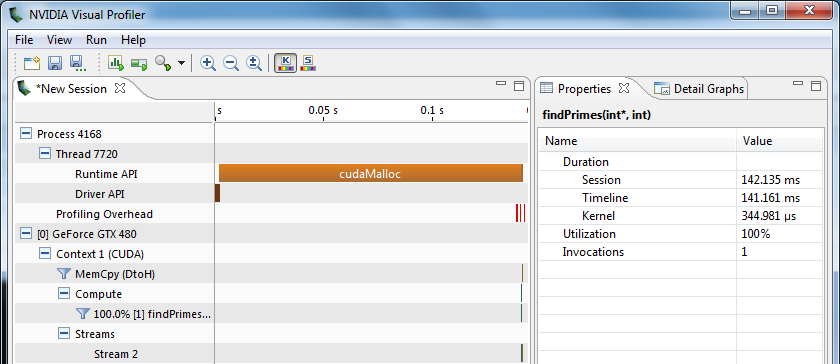
Sample output from A2, for demonstration:
Demonstration of how efficient A2 runs for n = 1,000 (for comparison, A1 took 20.78 seconds).
Assignment 1
Graeme Smyth
Topic
Making parallel an application which calculates the first n primes.
//DPS915 Assignment 1
//
//Graeme Smyth
//Code written by Graeme Smyth, with inspiration from course Workshop 1
//February 7th, 2013
#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <cmath>
#include <ctime>
using namespace std;
bool isPrime(int x)
{
for(int a = 0; a < x; a++) //a is any integer [0,x)
for(int b = 0; b < x; b++) //b is any integer [0,x)
if(a * b == x) //If a * b = x, then x has two integers that multiply to form it,
return false; //hence x is not prime
return true; //If we haven't returned by this point, x must be prime.
}
void findPrimes(int* answers, int n)
{
for(int i = 1, primesFound = 0; primesFound < n; i++) //Keep going until we have found n primes
if(isPrime(i)) //Test if "i" is prime
answers[primesFound++] = i; //If it is, record it
}
//Main takes one argument, integer n, and calculates the first n primes.
int main(int argc, char* argv[])
{
time_t timeStart, timeEnd;
//Check argument count
if (argc != 2)
{
cerr << "**invalid number of arguments**" << endl;
return 1;
}
int n = atoi(argv[1]);
int* answers = new int[n];
timeStart = time(nullptr); //Start timing
findPrimes(answers, n);
timeEnd = time(nullptr); //Finish timing
delete answers;
cout << setprecision(3);
cout << "Elapsed time : " << difftime(timeEnd, timeStart) << endl;
}
Roman Hotin
Topic
encrypting text
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cstring>
#include <string>
#include <cctype>
using namespace std;
void Encrypt(string&);
string Decrypt(string strTarget);
int main(int argc, char* argv[]) {
//initialize and get the string from the user
string strTarget;
cout << "Enter a string to encrypt: ";
//getline(cin,strTarget);
strTarget = argv[1];
string temp(strTarget);
Encrypt(strTarget);
cout << "Encrypted: " << strTarget << endl;
cout << "Decrypted: " << Decrypt(strTarget) << endl;
return 0;
}
void Encrypt(string &strTarget)
{
int len = strTarget.length();
char a;
string strFinal(strTarget);
for (int i = 0; i <= (len-1); i++)
{
a = strTarget.at(i);
int b = (int)a; //get the ASCII value of 'a'
b += 2; //Mulitply the ASCII value by 2
if (b > 254) { b = 254; }
a = (char)b; //Set the new ASCII value back into the char
strFinal.insert(i , 1, a); //Insert the new Character back into the string
}
string strEncrypted(strFinal, 0, len);
strTarget = strEncrypted;
}
string Decrypt(string strTarget)
{
int len = strTarget.length();
char a;
string strFinal(strTarget);
for (int i = 0; i <= (len-1); i++)
{
a = strTarget.at(i);
int b = (int)a;
b -= 2;
a = (char)b;
strFinal.insert(i, 1, a);
}
string strDecrypted(strFinal, 0, len);
return strDecrypted;
}