Difference between revisions of "Team Sonic"

From CDOT Wiki
Jump to: navigation, search
(→‎Team Sonic)
 
(24 intermediate revisions by 3 users not shown)
Line 1: Line 1:
 
= Team Sonic =
 
= Team Sonic =
−
[[Image:sonicteam.png|right|frameless|widthpx| ]]
+
[[Image:sonicteam.png|right|frameless|727| ]]
 
== Members ==  
 
== Members ==  
 
# [mailto:pvaaheeswaran@senecacollege.ca?subject=gpu610 Prasanth Vaaheeswaran]
 
# [mailto:pvaaheeswaran@senecacollege.ca?subject=gpu610 Prasanth Vaaheeswaran]
 
# [mailto:dlev1@myseneca.ca?subject=GPU610 Daniel Lev]
 
# [mailto:dlev1@myseneca.ca?subject=GPU610 Daniel Lev]
−
# [mailto:vturalba@myseneca.ca?subject=GPU610 Leo Turalba]
+
<!-- # [mailto:vturalba@myseneca.ca?subject=GPU610 Leo Turalba] -->
−
:[mailto:pvaaheeswaran@senecacollege.ca,dlev1@myseneca.ca,vturalba@myseneca.ca?subject=gpu610 Email All]
+
:[mailto:pvaaheeswaran@senecacollege.ca,dlev1@myseneca.ca?subject=gpu610 Email All]
  
 
== About ==  
 
== About ==  
 +
== Required Files ==
  
−
 
+
#[http://www5.cs.fau.de/research/projects/rabbitct/download/ RabbitCT]
 +
#[http://www5.cs.fau.de/fileadmin/Forschung/Software/RabbitCT/download/rabbitct_512-v2.rctd Dataset (Included problem sizes: 128, 256, 512)]
 
== Progress ==
 
== Progress ==
 
=== Assignment 1 ===
 
=== Assignment 1 ===
Line 16: Line 18:
 
I'm interested in profiling and parallelizing an algorithm that finds the average value of an array of integral values. Although it might not sound exciting to some, I think it's a great starting point.
 
I'm interested in profiling and parallelizing an algorithm that finds the average value of an array of integral values. Although it might not sound exciting to some, I think it's a great starting point.
  
 +
=====Updates=====
 
Feb 6: I created a program that does what I specified. I profiled it, and the profile showed that my application spends most of its time in the init_and_avg() function. That function has a loop that can be parallelized because each iteration is independent.
 
Feb 6: I created a program that does what I specified. I profiled it, and the profile showed that my application spends most of its time in the init_and_avg() function. That function has a loop that can be parallelized because each iteration is independent.
−
=====Updates=====
 
 
====[[User:Pvaaheeswaran | Prasanth]]====
 
====[[User:Pvaaheeswaran | Prasanth]]====
 
=====Topic=====
 
=====Topic=====
 
Find open source tomography algorithm, profile it, then attempt to convert parts of source code to take advantage of GPU using CUDA.
 
Find open source tomography algorithm, profile it, then attempt to convert parts of source code to take advantage of GPU using CUDA.
−
=====Updates=====
+
=====Update=====
 +
======Project======
 +
I have found an open source project called [http://www5.cs.fau.de/research/projects/rabbitct/ RabbitCT] which aims to support the creation of efficient algorithms to process voxel data. The ultimate goal is to improve the performance of 3-D cone beam reconstruction, which is used extensively in the medical field to processing cone bean computed tomography. "Cone bean computed tomography (CT) is an emerging imaging technology. It provides all projections needed for three-dimensional (3D) reconstruction in a single spin of the X- ray source-detector pair. This facilitates fast, low-dose data acquisition, which is required for the imaging of rapidly moving objects, such as the human heart, as well as for intra-operative CT applications." [[http://www.cs.sunysb.edu/~mueller/research/art/ Klaus Mueller]]
 +
======Profiling======
 +
After many many(!) issues, I was able to profile the reconstruction algorithm on my laptop.
 +
 
 +
RabbitCT provides three files:
 +
# '''RabbitCTRunner''' - the application that accepts the data-set and algorithm module and gives some basic metrics of algorithm performance (i.e. elapsed time)
 +
# R'''abbitCT Dataset V2''' - platform independent data-set of actual C-arm scan of rabbit (~2.5Gb for "small" ver)
 +
# '''LolaBunny''' - a basic non-optimized reference algorithm module (shared library)
 +
 
 +
Since the main processing is offloaded to the shared library (or dll on windows) I can't simply compile and run gprof on the main application (RabbitCTRunner), I had to set some special settings in shell to profile a shared library and use '''sprof'''; gprof can not be used for profiling shared libraries (found this out the hard long way). After many failed attempts these following steps allowed me to get a flat profile of the module.
 +
 
 +
Steps to reproduce:
 +
# run cmake and create executables RabbitCTRunner and the share library LolaBunny
 +
# $LD_PROFILE=libLolaBunny.so ./RabbitCTRunner [LOCATION OF MODULE] [LOCATION OF DATA-SET] [REPORT FILE] [VOLUMLE SIZE] <br />'''Example:''' LD_PROFILE=libLolaBunny.so ./RabbitCTRunner ../modules/LolaBunny/libLolaBunny.so ~/datasets/rabbitct_512-v2.rctd ./resultFile 128
 +
# $ sprof -p [LOCATION OF MODULE] [LOCATION OF PROFILE FILE] > log <BR />'''Example:''' sprof -p ../modules/LolaBunny/libLolaBunny.so /var/tmp/libLolaBunny.so.profile > log <br />'''Note.''' /var/tmp/ was my default location for profiles. Man ld.so for LD_PROFILE_EXPORT
 +
 
 +
You should now have a log file in your current dir, which has a flat-profile of the module: (Note. This was run with the smallest possible volume size, running it at 512 or higher takes much much longer)
 +
 
 +
<pre>
 +
[prasanth@localhost RabbitCTRunner]$ cat log
 +
Flat profile:
 +
 
 +
Each sample counts as 0.01 seconds.
 +
  %  cumulative  self              self    total
 +
time  seconds  seconds    calls  us/call  us/call  name
 +
100.00    112.58  112.58        0    0.00          RCTAlgorithmBackprojection
 +
 
 +
</pre>
 +
 
 +
This is the output from RabbitCTRunner:
 +
<pre>
 +
[prasanth@localhost RabbitCTRunner]$ LD_PROFILE=libLolaBunny.so ./RabbitCTRunner ../modules/LolaBunny/libLolaBunny.so ~/datasets/rabbitct_512-v2.rctd ./resultFile 128
 +
RabbitCT runner http://www.rabbitct.com/
 +
Info: using 4 buffer subsets with 240 projections each.
 +
Running ... this may take some time.
 +
  (\_/)
 +
(='.'=)
 +
(")_(")
 +
 
 +
--------------------------------------------------------------
 +
Quality of reconstructed volume:
 +
Root Mean Squared Error: 38914.3 HU
 +
Mean Squared Error: 1.51433e+09 HU^2
 +
Max. Absolute Error: 65535 HU
 +
PSNR: -19.5571 dB
 +
 
 +
--------------------------------------------------------------
 +
Runtime statistics:
 +
Total:  112.627 s
 +
Average: 117.32 ms
 +
 
 +
</pre>
 +
 
 +
======Summary======
 +
With the flat-profile data, I can say with some certainty that 100% of the time is spent on the 'RCTAlgorithmBackprojection' method. Digging in to the source code this is the actual code of this method:
 +
 
 +
''LolaBunny.cpp''
 +
<pre>
 +
FNCSIGN bool RCTAlgorithmBackprojection(RabbitCtGlobalData* r)
 +
{
 +
    unsigned int L  = r->L;
 +
    float        O_L = r->O_L;
 +
    float        R_L = r->R_L;
 +
    double*      A_n = r->A_n;
 +
    float*      I_n = r->I_n;
 +
    float*      f_L = r->f_L;
 +
 +
    s_rcgd = r;
 +
 +
    for (unsigned int k=0; k<L; k++)
 +
    {
 +
        double z = O_L + (double)k * R_L;
 +
        for (unsigned int j=0; j<L; j++)
 +
        {
 +
            double y = O_L + (double)j * R_L;
 +
            for (unsigned int i=0; i<L; i++)
 +
            {
 +
                double x = O_L + (double)i * R_L;
 +
 +
                double w_n =  A_n[2] * x + A_n[5] * y + A_n[8] * z + A_n[11];
 +
                double u_n = (A_n[0] * x + A_n[3] * y + A_n[6] * z + A_n[9] ) / w_n;
 +
                double v_n = (A_n[1] * x + A_n[4] * y + A_n[7] * z + A_n[10]) / w_n;
 +
 +
                f_L[k * L * L + j * L + i] += (float)(1.0 / (w_n * w_n) * p_hat_n(u_n, v_n));
 +
            }
 +
        }
 +
    }
 +
 +
    return true;
 +
}
 +
</pre>
 +
 
 +
We can see there is a nested for loop, containing three for loops. In Big-O notation the order of growth for this method would be O(N3). It is also using double precision and matrix multiplications, therefore I think this code can be optimized using CUDA.
 +
These results here were calculated on a:
 +
<pre>
 +
Lenovo T400 laptop
 +
Intel® Core™2 Duo CPU P8600 @ 2.40GHz × 2
 +
4GB 1066 MHz Memory
 +
Fedora Release 18 (Spherical Cow) 64-bit
 +
Kernel: 3.6.10-4.fc18.x86_64
 +
</pre>
 +
I'm sure running this on our GTX 480 can yield better results. (hopefully).
 +
<!--
 
====[[User:Leo_Turalba | Leo]]====
 
====[[User:Leo_Turalba | Leo]]====
 
=====Topic=====
 
=====Topic=====
Line 30: Line 136:
  
 
=====Updates=====
 
=====Updates=====
 +
-->
 +
=== Assignment 2 ===
 +
 +
=====Background=====
 +
In assignment 1 we identified the 'RCTAlgorithmBackprojection' function located in the dll/shared library was taking up virtually 100% of the execution time. Our goal for this assignment was to off-load that logic to the GPU using cuda api, leaving everything else intact. 
 +
=====Process=====
 +
The work we did can be separated in to three basic steps:
 +
#Compile base software from source (RabbitCTRunner.exe and dll)
 +
#Write cuda kernel to replace 'RCTAlgorithmBackprojection' in dll
 +
#Integrate cuda kernel in to RabbitCTRunner
 +
Using preprocessor directives the RabbitCTRunner was fitted with a token named GPU. If GPU was defined, our kernel along with all the necessary code will be compiled and used by RabbitCTRunner. This allowed us to have a small footprint on the changes applied and also allows us to use the flag to compile back the original RabbitCTRunner.
 +
 +
======Kernel======
 +
 +
<pre>
 +
__global__
 +
void Backprojection(float * gpu_matrix_result, RabbitCtGlobalData * r) // problem_size is r.L
 +
 +
    {
 +
    unsigned int L  = r->L;
 +
    float        O_L = r->O_L;
 +
    float        R_L = r->R_L;
 +
    double*      A_n = r->A_n;
 +
    //float*      I_n = r->I_n;
 +
    //float*      f_L = r->f_L;
 +
    // for optimization, put these ^ in shared memory.
 +
 +
    //s_rcgd = r;
 +
 +
    unsigned int col = blockDim.x * blockIdx.x + threadIdx.x; // this is like the original "i" iterator
 +
    unsigned int row = blockDim.y * blockIdx.y + threadIdx.y; // this is like the original "j" iterator
 +
    unsigned int depth = blockDim.z * blockIdx.z + threadIdx.z; // this is like the original "k" iterator
 +
 +
    if (row < L && col < L && depth < L)
 +
        {
 +
        unsigned int final_index = L * L * depth + L * row + col;
 +
        double z = O_L + (double)depth * R_L;
 +
        double y = O_L + (double)row * R_L;
 +
        double x = O_L + (double)col * R_L;
 +
 +
        double w_n =  A_n[2] * x + A_n[5] * y + A_n[8] * z + A_n[11];
 +
        double u_n = (A_n[0] * x + A_n[3] * y + A_n[6] * z + A_n[9] ) / w_n; // inline this
 +
        double v_n = (A_n[1] * x + A_n[4] * y + A_n[7] * z + A_n[10]) / w_n; // inline this
 +
 +
        // p_hat_n inlined:
 +
        int i = (int)u_n;
 +
        int j = (int)v_n;
 +
        double alpha = u_n - (int)u_n;
 +
        double beta  = v_n - (int)v_n;
 +
        double p_hat_n_result =
 +
            (1.0 - alpha) * (1.0 - beta) * p_n(i  , j  )
 +
            +        alpha  * (1.0 - beta) * p_n(i+1, j  )
 +
            + (1.0 - alpha) *        beta  * p_n(i  , j+1)
 +
            +        alpha  *        beta  * p_n(i+1, j+1);
 +
        ///////
 +
 +
        gpu_matrix_result[final_index] += (float)(1.0 / (w_n * w_n) * p_hat_n_result);
 +
 +
 +
        // this call calculates the index value twice because of +=
 +
        }
 +
    }
 +
</pre>
 +
======Memory Allocation======
 +
<pre>
 +
#ifdef GPU
 +
    float * gpu_matrix;
 +
    cudaMalloc((void**)&gpu_matrix, numel_vol * sizeof(float));
 +
    cudaMemcpy(gpu_matrix, rctgdata.f_L, numel_vol * sizeof(float), cudaMemcpyHostToDevice);           
 +
    const int threads_per_block = 16;
 +
    const int num_of_blocks = (problem_size + threads_per_block - 1) / threads_per_block;
 +
    dim3 block(threads_per_block, threads_per_block, threads_per_block);
 +
    dim3 grid(num_of_blocks, num_of_blocks, num_of_blocks);
 +
#endif
 +
</pre>
 +
======Execution Config======
 +
<pre>
 +
#ifdef GPU
 +
            Backprojection<<<grid, block>>>(gpu_matrix, &rctgdata);           
 +
#else
 +
</pre>
 +
 +
=====Metrics=====
 +
Original RabbitCTRunner with volume size 128:
 +
<pre>
 +
C:\Users\pvaaheeswaran\Desktop\cuda rabbit>Rabbit.exe LolaBunny.dll rabbitct_512-v2.rctd original 128
 +
RabbitCT runner http://www.rabbitct.com/
 +
Info: using 4 buffer subsets with 240 projections each.
 +
Running ... this may take some time.
 +
  (\_/)
 +
(='.'=)
 +
(")_(")
 +
 +
--------------------------------------------------------------
 +
Quality of reconstructed volume:
 +
Root Mean Squared Error: 38914.3 HU
 +
Mean Squared Error: 1.51433e+009 HU^2
 +
Max. Absolute Error: 65535 HU
 +
PSNR: -19.5571 dB
 +
 +
--------------------------------------------------------------
 +
Runtime statistics:
 +
Total:  339.759 s
 +
Average: 353.915 ms
 +
 +
FULL RUNTIME: 340.507 secs
 +
C:\Users\pvaaheeswaran\Desktop\cuda rabbit>
 +
 +
</pre>
 +
 +
CudaRabbit, volume size 128.
 +
<pre>
 +
C:\Users\pvaaheeswaran\Desktop\cuda rabbit>CudaRabbit.exe LolaBunny.dll rabbitct_512-v2.rctd result 128/
 +
RabbitCT runner http://www.rabbitct.com/
 +
Info: using 4 buffer subsets with 240 projections each.
 +
Running ... this may take some time.
 +
  (\_/)
 +
(='.'=)
 +
(")_(")
 +
 +
--------------------------------------------------------------
 +
Quality of reconstructed volume:
 +
Root Mean Squared Error: 38914.3 HU
 +
Mean Squared Error: 1.51433e+009 HU^2
 +
Max. Absolute Error: 65535 HU
 +
PSNR: -19.5571 dB
 +
 +
--------------------------------------------------------------
 +
Runtime statistics:
 +
Total:  0.004881 s
 +
Average: 0.00508437 ms
 +
 +
FULL RUNTIME: 0.512 secs
 +
 +
C:\Users\pvaaheeswaran\Desktop\cuda rabbit>
 +
</pre>
 +
 +
=====Graph=====
 +
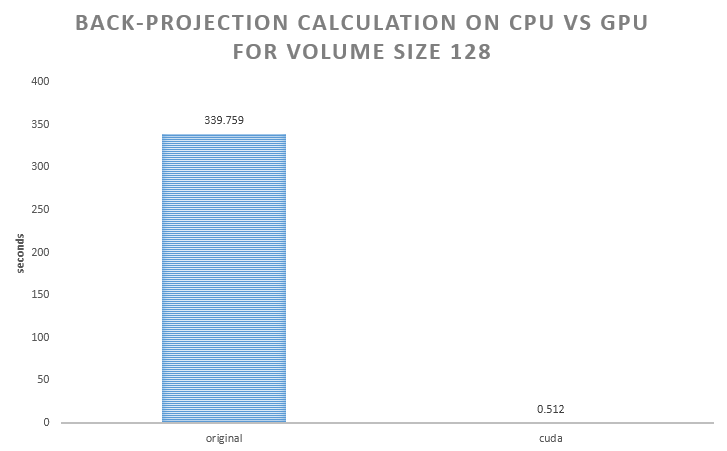
This graph represents for only 128 volume size.
 +
[[Image:sonicgraph1.png|left|frame]]
 +
=====Summary=====
 +
As you can see, using cuda has improved the performance by ~99.85%, we went from over 5 minutes to under a second. However, this code still needs to be optimized and run on bigger volume sizes. This will be our next goal.
  
−
=== Assignment 2 ===
 
 
=== Assignment 3 ===
 
=== Assignment 3 ===

Latest revision as of 22:35, 8 March 2013

Team Sonic

Sonicteam.png

Members

  1. Prasanth Vaaheeswaran
  2. Daniel Lev
Email All

About

Required Files

  1. RabbitCT
  2. Dataset (Included problem sizes: 128, 256, 512)

Progress

Assignment 1

Daniel

Topic

I'm interested in profiling and parallelizing an algorithm that finds the average value of an array of integral values. Although it might not sound exciting to some, I think it's a great starting point.

Updates

Feb 6: I created a program that does what I specified. I profiled it, and the profile showed that my application spends most of its time in the init_and_avg() function. That function has a loop that can be parallelized because each iteration is independent.

Prasanth

Topic

Find open source tomography algorithm, profile it, then attempt to convert parts of source code to take advantage of GPU using CUDA.

Update
Project

I have found an open source project called RabbitCT which aims to support the creation of efficient algorithms to process voxel data. The ultimate goal is to improve the performance of 3-D cone beam reconstruction, which is used extensively in the medical field to processing cone bean computed tomography. "Cone bean computed tomography (CT) is an emerging imaging technology. It provides all projections needed for three-dimensional (3D) reconstruction in a single spin of the X- ray source-detector pair. This facilitates fast, low-dose data acquisition, which is required for the imaging of rapidly moving objects, such as the human heart, as well as for intra-operative CT applications." [Klaus Mueller]

Profiling

After many many(!) issues, I was able to profile the reconstruction algorithm on my laptop.

RabbitCT provides three files:

  1. RabbitCTRunner - the application that accepts the data-set and algorithm module and gives some basic metrics of algorithm performance (i.e. elapsed time)
  2. RabbitCT Dataset V2 - platform independent data-set of actual C-arm scan of rabbit (~2.5Gb for "small" ver)
  3. LolaBunny - a basic non-optimized reference algorithm module (shared library)

Since the main processing is offloaded to the shared library (or dll on windows) I can't simply compile and run gprof on the main application (RabbitCTRunner), I had to set some special settings in shell to profile a shared library and use sprof; gprof can not be used for profiling shared libraries (found this out the hard long way). After many failed attempts these following steps allowed me to get a flat profile of the module.

Steps to reproduce:

  1. run cmake and create executables RabbitCTRunner and the share library LolaBunny
  2. $LD_PROFILE=libLolaBunny.so ./RabbitCTRunner [LOCATION OF MODULE] [LOCATION OF DATA-SET] [REPORT FILE] [VOLUMLE SIZE]
    Example: LD_PROFILE=libLolaBunny.so ./RabbitCTRunner ../modules/LolaBunny/libLolaBunny.so ~/datasets/rabbitct_512-v2.rctd ./resultFile 128
  3. $ sprof -p [LOCATION OF MODULE] [LOCATION OF PROFILE FILE] > log
    Example: sprof -p ../modules/LolaBunny/libLolaBunny.so /var/tmp/libLolaBunny.so.profile > log
    Note. /var/tmp/ was my default location for profiles. Man ld.so for LD_PROFILE_EXPORT

You should now have a log file in your current dir, which has a flat-profile of the module: (Note. This was run with the smallest possible volume size, running it at 512 or higher takes much much longer) 

[prasanth@localhost RabbitCTRunner]$ cat log
Flat profile:

Each sample counts as 0.01 seconds.
  %   cumulative   self              self     total
 time   seconds   seconds    calls  us/call  us/call  name
100.00    112.58   112.58        0     0.00           RCTAlgorithmBackprojection

This is the output from RabbitCTRunner: 

[prasanth@localhost RabbitCTRunner]$ LD_PROFILE=libLolaBunny.so ./RabbitCTRunner ../modules/LolaBunny/libLolaBunny.so ~/datasets/rabbitct_512-v2.rctd ./resultFile 128
RabbitCT runner http://www.rabbitct.com/
Info: using 4 buffer subsets with 240 projections each.
Running ... this may take some time.
  (\_/)
 (='.'=)
 (")_(")

--------------------------------------------------------------
Quality of reconstructed volume:
Root Mean Squared Error: 38914.3 HU
Mean Squared Error: 1.51433e+09 HU^2
Max. Absolute Error: 65535 HU
PSNR: -19.5571 dB

--------------------------------------------------------------
Runtime statistics:
Total:   112.627 s
Average: 117.32 ms
Summary

With the flat-profile data, I can say with some certainty that 100% of the time is spent on the 'RCTAlgorithmBackprojection' method. Digging in to the source code this is the actual code of this method:

LolaBunny.cpp 

FNCSIGN bool RCTAlgorithmBackprojection(RabbitCtGlobalData* r)
{
    unsigned int L   = r->L;
    float        O_L = r->O_L;
    float        R_L = r->R_L;
    double*      A_n = r->A_n;
    float*       I_n = r->I_n;
    float*       f_L = r->f_L;
 
    s_rcgd = r;
 
    for (unsigned int k=0; k<L; k++)
    {
        double z = O_L + (double)k * R_L;
        for (unsigned int j=0; j<L; j++)
        {
            double y = O_L + (double)j * R_L;
            for (unsigned int i=0; i<L; i++)
            {
                double x = O_L + (double)i * R_L;
 
                double w_n =  A_n[2] * x + A_n[5] * y + A_n[8] * z + A_n[11];
                double u_n = (A_n[0] * x + A_n[3] * y + A_n[6] * z + A_n[9] ) / w_n;
                double v_n = (A_n[1] * x + A_n[4] * y + A_n[7] * z + A_n[10]) / w_n;
 
                f_L[k * L * L + j * L + i] += (float)(1.0 / (w_n * w_n) * p_hat_n(u_n, v_n)); 
            }
        }
    }
 
    return true;
}

We can see there is a nested for loop, containing three for loops. In Big-O notation the order of growth for this method would be O(N3). It is also using double precision and matrix multiplications, therefore I think this code can be optimized using CUDA. These results here were calculated on a: 

Lenovo T400 laptop
Intel® Core™2 Duo CPU P8600 @ 2.40GHz × 2
4GB 1066 MHz Memory
Fedora Release 18 (Spherical Cow) 64-bit 
Kernel: 3.6.10-4.fc18.x86_64

I'm sure running this on our GTX 480 can yield better results. (hopefully).

Assignment 2

Background

In assignment 1 we identified the 'RCTAlgorithmBackprojection' function located in the dll/shared library was taking up virtually 100% of the execution time. Our goal for this assignment was to off-load that logic to the GPU using cuda api, leaving everything else intact.

Process

The work we did can be separated in to three basic steps:

  1. Compile base software from source (RabbitCTRunner.exe and dll)
  2. Write cuda kernel to replace 'RCTAlgorithmBackprojection' in dll
  3. Integrate cuda kernel in to RabbitCTRunner

Using preprocessor directives the RabbitCTRunner was fitted with a token named GPU. If GPU was defined, our kernel along with all the necessary code will be compiled and used by RabbitCTRunner. This allowed us to have a small footprint on the changes applied and also allows us to use the flag to compile back the original RabbitCTRunner.

Kernel
__global__ 
void Backprojection(float * gpu_matrix_result, RabbitCtGlobalData * r) // problem_size is r.L

    {
    unsigned int L   = r->L;
    float        O_L = r->O_L;
    float        R_L = r->R_L;
    double*      A_n = r->A_n;
    //float*       I_n = r->I_n;
    //float*       f_L = r->f_L;
    // for optimization, put these ^ in shared memory. 

    //s_rcgd = r;

    unsigned int col = blockDim.x * blockIdx.x + threadIdx.x; // this is like the original "i" iterator
    unsigned int row = blockDim.y * blockIdx.y + threadIdx.y; // this is like the original "j" iterator
    unsigned int depth = blockDim.z * blockIdx.z + threadIdx.z; // this is like the original "k" iterator

    if (row < L && col < L && depth < L)
        {
        unsigned int final_index = L * L * depth + L * row + col;
        double z = O_L + (double)depth * R_L;
        double y = O_L + (double)row * R_L;
        double x = O_L + (double)col * R_L;

        double w_n =  A_n[2] * x + A_n[5] * y + A_n[8] * z + A_n[11];
        double u_n = (A_n[0] * x + A_n[3] * y + A_n[6] * z + A_n[9] ) / w_n; // inline this
        double v_n = (A_n[1] * x + A_n[4] * y + A_n[7] * z + A_n[10]) / w_n; // inline this

        // p_hat_n inlined:
        int i = (int)u_n;
        int j = (int)v_n;
        double alpha = u_n - (int)u_n;
        double beta  = v_n - (int)v_n;
        double p_hat_n_result = 
            (1.0 - alpha) * (1.0 - beta) * p_n(i  , j  )
            +        alpha  * (1.0 - beta) * p_n(i+1, j  )
            + (1.0 - alpha) *        beta  * p_n(i  , j+1)
            +        alpha  *        beta  * p_n(i+1, j+1);
        ///////

        gpu_matrix_result[final_index] += (float)(1.0 / (w_n * w_n) * p_hat_n_result);


        // this call calculates the index value twice because of +=
        }
    }
Memory Allocation
#ifdef GPU
    float * gpu_matrix;
    cudaMalloc((void**)&gpu_matrix, numel_vol * sizeof(float));
    cudaMemcpy(gpu_matrix, rctgdata.f_L, numel_vol * sizeof(float), cudaMemcpyHostToDevice);            
    const int threads_per_block = 16;
    const int num_of_blocks = (problem_size + threads_per_block - 1) / threads_per_block;
    dim3 block(threads_per_block, threads_per_block, threads_per_block);
    dim3 grid(num_of_blocks, num_of_blocks, num_of_blocks);
#endif
Execution Config
#ifdef GPU
            Backprojection<<<grid, block>>>(gpu_matrix, &rctgdata);            
#else
Metrics

Original RabbitCTRunner with volume size 128: 

C:\Users\pvaaheeswaran\Desktop\cuda rabbit>Rabbit.exe LolaBunny.dll rabbitct_512-v2.rctd original 128
RabbitCT runner http://www.rabbitct.com/
Info: using 4 buffer subsets with 240 projections each.
Running ... this may take some time.
  (\_/)
 (='.'=)
 (")_(")

--------------------------------------------------------------
Quality of reconstructed volume:
Root Mean Squared Error: 38914.3 HU
Mean Squared Error: 1.51433e+009 HU^2
Max. Absolute Error: 65535 HU
PSNR: -19.5571 dB

--------------------------------------------------------------
Runtime statistics:
Total:   339.759 s
Average: 353.915 ms

FULL RUNTIME: 340.507 secs
C:\Users\pvaaheeswaran\Desktop\cuda rabbit>

CudaRabbit, volume size 128. 

C:\Users\pvaaheeswaran\Desktop\cuda rabbit>CudaRabbit.exe LolaBunny.dll rabbitct_512-v2.rctd result 128/
RabbitCT runner http://www.rabbitct.com/
Info: using 4 buffer subsets with 240 projections each.
Running ... this may take some time.
  (\_/)
 (='.'=)
 (")_(")

--------------------------------------------------------------
Quality of reconstructed volume:
Root Mean Squared Error: 38914.3 HU
Mean Squared Error: 1.51433e+009 HU^2
Max. Absolute Error: 65535 HU
PSNR: -19.5571 dB

--------------------------------------------------------------
Runtime statistics:
Total:   0.004881 s
Average: 0.00508437 ms

FULL RUNTIME: 0.512 secs

C:\Users\pvaaheeswaran\Desktop\cuda rabbit>
Graph

This graph represents for only 128 volume size.

Sonicgraph1.png
Summary

As you can see, using cuda has improved the performance by ~99.85%, we went from over 5 minutes to under a second. However, this code still needs to be optimized and run on bigger volume sizes. This will be our next goal.

Assignment 3

Retrieved from "https://wiki.cdot.senecapolytechnic.ca/w/index.php?title=Team_Sonic&oldid=94502"