Difference between revisions of "Kernal Blas"
(→Assignment 3) |
(→Progress) |
||
| (38 intermediate revisions by 2 users not shown) | |||
| Line 11: | Line 11: | ||
==== Calculation of Pi ==== | ==== Calculation of Pi ==== | ||
For this assessment, we used code found at [https://helloacm.com/cc-coding-exercise-finding-approximation-of-pi-using-monto-carlo-algorithm/ helloacm.com] | For this assessment, we used code found at [https://helloacm.com/cc-coding-exercise-finding-approximation-of-pi-using-monto-carlo-algorithm/ helloacm.com] | ||
| + | <syntaxhighlight lang="cpp"> | ||
| + | int main() { | ||
| + | srand(time(NULL)); | ||
| + | cout.precision(10); | ||
| + | std::chrono::steady_clock::time_point ts, te; | ||
| + | const double N[] = {1e1,1e3, 1e4, 1e5, 1e6, 1e7, 1e8}; | ||
| + | for (int j = 0; j < (sizeof(N) / sizeof(N[0])); j ++) { | ||
| + | ts = std::chrono::steady_clock::now(); | ||
| + | int circle = 0; | ||
| + | for (int i = 0; i < N[j]; i ++) { | ||
| + | double x = static_cast<double>(rand()) / static_cast<double>(RAND_MAX); | ||
| + | double y = static_cast<double>(rand()) / static_cast<double>(RAND_MAX); | ||
| + | if (x * x + y * y <= 1.0) circle ++; | ||
| + | } | ||
| + | te = std::chrono::steady_clock::now(); | ||
| + | cout << N[j] << (char)9 << (char)9 << (double)circle / N[j] * 4 ; | ||
| + | reportTime("", te - ts); | ||
| + | } | ||
| + | return 0; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
In this version, the value of PI is calculated using the Monte Carlo method. | In this version, the value of PI is calculated using the Monte Carlo method. | ||
This method states: | This method states: | ||
# A circle with radius '''r''' in a squre with side length '''2''r''''' | # A circle with radius '''r''' in a squre with side length '''2''r''''' | ||
| − | # The area of the circle is ''' | + | # The area of the circle is '''πr<sup>2</sup>''' and the area of the square is '''4r<sup>2</sup>''' |
| − | # The ratio of the area of the circle to the area of the square is: ''' | + | # The ratio of the area of the circle to the area of the square is: '''πr<sup>2</sup> / 4r<sup>2</sup> = π / 4''' |
| − | # If you randomly generate '''N''' points inside the square, approximately '''N * | + | # If you randomly generate '''N''' points inside the square, approximately '''N * π / 4''' of those points ('''M''') should fall inside the circle. |
| − | # ''' | + | # '''π''' is then approximated as: |
| − | ::* '''N * | + | ::* '''N * π / 4 = M ''' |
| − | ::* ''' | + | ::* '''π / 4 = M / N''' |
| − | ::* ''' | + | ::* '''π = 4 * M / N''' |
| + | |||
| + | In other words <br> | ||
| + | '''π ≈ 4 * Ninner / Ntotal''' | ||
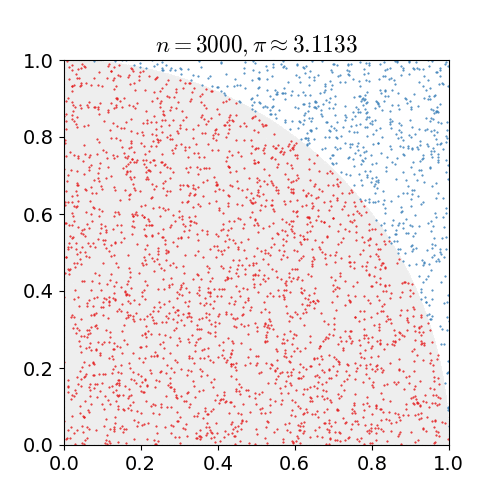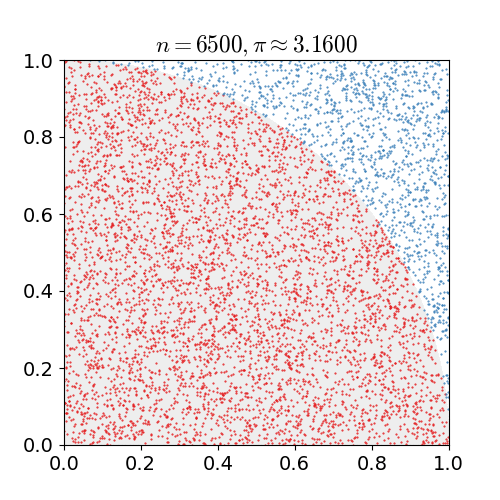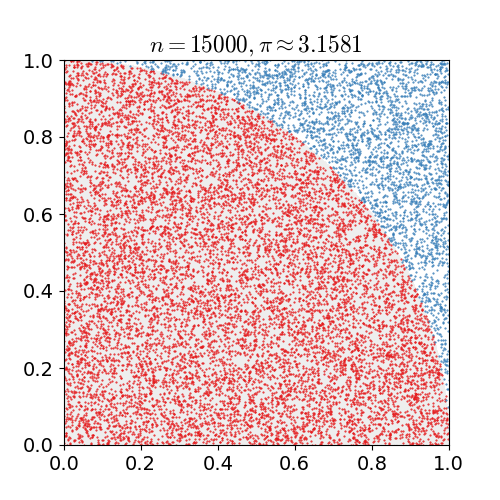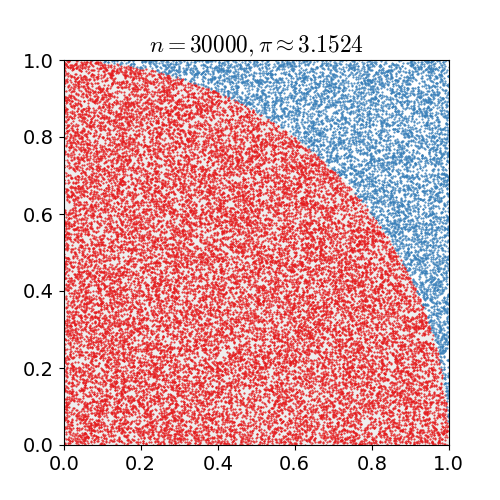
For simplicity the radius of the circle is 1. | For simplicity the radius of the circle is 1. | ||
| − | With this, we randomly generate points within the area and count the number of times each point falls within the circle, between 0 and 1. We then calculate the ratio and | + | With this, we randomly generate points within the area and count the number of times each point falls within the circle, between 0 and 1.<br> |
| + | We then calculate the ratio and | ||
multiply by 4 which will give us the approximation of Π. | multiply by 4 which will give us the approximation of Π. | ||
| + | When we only have a small number of points, the estimation is not very accurate,<br> | ||
| + | but when we have hundreds of thousands of points, we get much closer to the actual value.<br> | ||
| + | [[File:Pi 30K.gif]] | ||
When we run the program we see: | When we run the program we see: | ||
| Line 38: | Line 66: | ||
100000000 3.1419176 - took - 10035 millisecs | 100000000 3.1419176 - took - 10035 millisecs | ||
| − | ''The first column represents | + | ''The first column represents the number of points we are generating |
With this method, we can see that the accuracy of the calculation is slightly off. This is due to the randomization of points within the circle. Running the program again will give us slightly different results. | With this method, we can see that the accuracy of the calculation is slightly off. This is due to the randomization of points within the circle. Running the program again will give us slightly different results. | ||
| Line 51: | Line 79: | ||
The hotspot within the code lies in the loops. There iteration for the loops is O(n<sup>2</sup>) | The hotspot within the code lies in the loops. There iteration for the loops is O(n<sup>2</sup>) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==== Data Compression ==== | ==== Data Compression ==== | ||
| Line 118: | Line 133: | ||
'''Parallelizing | '''Parallelizing | ||
| − | + | We did not see any other way to parallelize the algorithm. | |
| − | + | === Assignment 2 === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ---- | |
| − | |||
In order to parallelize the code from above, we decided to use a kernel to handle the calculations. | In order to parallelize the code from above, we decided to use a kernel to handle the calculations. | ||
| − | The logic remains the same but the | + | The logic largely remains the same, but we offload the CPU calculations to the GPU. <br> |
| + | This code generates random points within the kernel and the calculations are also done in here. <br> | ||
<br> | <br> | ||
Offloading to the GPU results in a pi calculation time to be reduced | Offloading to the GPU results in a pi calculation time to be reduced | ||
<br> | <br> | ||
| − | |||
<br> | <br> | ||
'''Kernel code used | '''Kernel code used | ||
| Line 140: | Line 150: | ||
<syntaxhighlight lang="cpp"> | <syntaxhighlight lang="cpp"> | ||
| − | __global__ void calculate(float * | + | __global__ void calculate(float *d_pi, curandState *states, float n) { |
| − | int | + | unsigned int tid = threadIdx.x + blockDim.x * blockIdx.x; |
| − | + | float points = 0; | |
| − | + | float x, y; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | float | ||
| − | |||
| − | + | curand_init(1000, tid, 0, &states[tid]); // Initialize CURAND | |
| − | |||
| − | |||
| − | |||
| − | + | for (int i = 0; i < n; i++) { | |
| − | + | x = curand_uniform(&states[tid]); //calls random float from 0.0 to 1.0 | |
| − | + | y = curand_uniform(&states[tid]); | |
| − | + | points += (x*x + y*y <= 1.0f); // count if x & y is in the circle. | |
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | + | d_pi[tid] = 4.0f * points / n; // return estimate of pi | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | <br> | ||
| + | [http://docs.nvidia.com/cuda/curand/index.html cuRAND] documentation. | ||
| + | <br> | ||
| + | |||
'''Results CPU vs GPU | '''Results CPU vs GPU | ||
<br> | <br> | ||
| − | [[File:Cpuvsgpusheet.PNG]] | + | [[File:Cpuvsgpusheet.PNG|600px]] |
<br> | <br> | ||
<br> | <br> | ||
| − | [[File:Cpuvsgpu.png]] | + | [[File:Cpuvsgpu.png|600px]] |
<br> | <br> | ||
As we can see above, the more iterations, the more accurate the calculation of PI. <br> | As we can see above, the more iterations, the more accurate the calculation of PI. <br> | ||
The CPU's results drastically change as we increase the iteration 10x. <br> | The CPU's results drastically change as we increase the iteration 10x. <br> | ||
However, the parallelized results seem to stay accurate throughout the iterations. <br> | However, the parallelized results seem to stay accurate throughout the iterations. <br> | ||
| − | + | It seems as though the calculation time doesn't change much and stays consistent. <br> | |
| − | + | [[File:Cudamalloc.PNG|800px]] <br> | |
| − | + | [[File:Prof.PNG]] <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Profiling the code shows that '''cudaMalloc''' takes up most of the time spent. Even when <br> | |
| − | + | there are 10 iterations, the time remains at 300 milliseconds. <br> | |
| − | + | As the iteration passes 25 million, we have a bit of memory leak which results in inaccurate results. <br><br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In order to optimize the code, we must find a way reduce the time cudaMalloc takes.<br> | ||
| − | + | === Assignment 3 === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ---- | |
| − | + | After realizing the cudaMemcpy and cudaMalloc takes quite a bit of time, we focused our efforts on optimizing it. | |
| − | + | It was difficult to find a solution because the initial copy takes a bit of time to set up.<br> | |
| − | + | We tried using cudaMallocHost to see if we can allocate memory instead of using malloc. <br> | |
| − | + | cudaMallocHost will allocate pinned memory which is stored in RAM and can be accessed by the GPU's DMA directly. | |
| − | + | We changed one part of our code | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <syntaxhighlight lang="cpp"> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | cudaMallocHost((void **)&host, size); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | </syntaxhighlight> | |
| − | |||
| − | |||
| − | |||
| − | + | <br/> | |
| − | + | <br/> | |
| + | Here we can see where an error occurs, we suspect that a memory leak causes the problem resulting in an error in pi calculation | ||
| − | + | '''Optimized time run results | |
| − | + | <br> | |
| − | + | [[File:Chart3.PNG]]<br> | |
| − | + | [[File:Chartp3.PNG]]<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | + | The final results show that although cudaMallocHost should imporve the speed of memory transfer, if didn't make much <br> | |
| + | of a difference here. In conclusion, we can see that the GPU performance is significantly faster than the CPU's performance.<br> | ||
Latest revision as of 09:14, 4 April 2018
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
Kernal Blas
Team Members
Progress
Assignment 1
Calculation of Pi
For this assessment, we used code found at helloacm.com
int main() {
srand(time(NULL));
cout.precision(10);
std::chrono::steady_clock::time_point ts, te;
const double N[] = {1e1,1e3, 1e4, 1e5, 1e6, 1e7, 1e8};
for (int j = 0; j < (sizeof(N) / sizeof(N[0])); j ++) {
ts = std::chrono::steady_clock::now();
int circle = 0;
for (int i = 0; i < N[j]; i ++) {
double x = static_cast<double>(rand()) / static_cast<double>(RAND_MAX);
double y = static_cast<double>(rand()) / static_cast<double>(RAND_MAX);
if (x * x + y * y <= 1.0) circle ++;
}
te = std::chrono::steady_clock::now();
cout << N[j] << (char)9 << (char)9 << (double)circle / N[j] * 4 ;
reportTime("", te - ts);
}
return 0;
}In this version, the value of PI is calculated using the Monte Carlo method. This method states:
- A circle with radius r in a squre with side length 2r
- The area of the circle is πr2 and the area of the square is 4r2
- The ratio of the area of the circle to the area of the square is: πr2 / 4r2 = π / 4
- If you randomly generate N points inside the square, approximately N * π / 4 of those points (M) should fall inside the circle.
- π is then approximated as:
- N * π / 4 = M
- π / 4 = M / N
- π = 4 * M / N
In other words
π ≈ 4 * Ninner / Ntotal
For simplicity the radius of the circle is 1.
With this, we randomly generate points within the area and count the number of times each point falls within the circle, between 0 and 1.
We then calculate the ratio and
multiply by 4 which will give us the approximation of Π.
When we only have a small number of points, the estimation is not very accurate,
but when we have hundreds of thousands of points, we get much closer to the actual value.
When we run the program we see:
1st Run
1000 3.152 - took - 0 millisecs 10000 3.1328 - took - 0 millisecs 100000 3.14744 - took - 9 millisecs 1000000 3.141028 - took - 96 millisecs 10000000 3.1417368 - took - 998 millisecs 100000000 3.1419176 - took - 10035 millisecs The first column represents the number of points we are generating
With this method, we can see that the accuracy of the calculation is slightly off. This is due to the randomization of points within the circle. Running the program again will give us slightly different results.
2nd Run
1000 3.12 - took - 0 millisecs 10000 3.1428 - took - 0 millisecs 100000 3.13528 - took - 9 millisecs 1000000 3.143348 - took - 106 millisecs 10000000 3.1414228 - took - 1061 millisecs 100000000 3.14140056 - took - 8281 millisecs
The hotspot within the code lies in the loops. There iteration for the loops is O(n2)
Data Compression
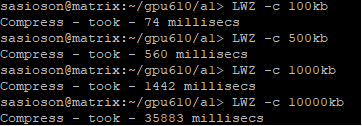
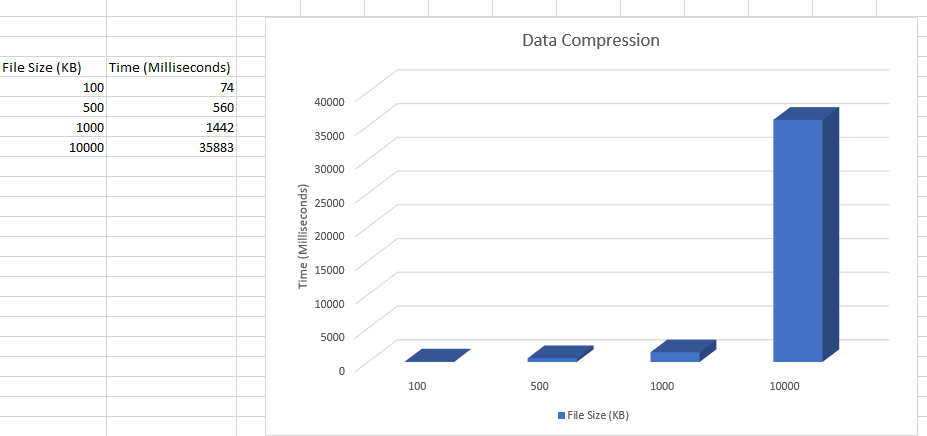
For this suggested project we used the LZW algorithm from one of the suggested projects.
The compress dictionary copies the file into a new file with a .LZW filetype which uses ASCII
The function that compresses the file initializing with ASCII
void compress(string input, int size, string filename) {
unordered_map<string, int> compress_dictionary(MAX_DEF);
//Dictionary initializing with ASCII
for (int unsigned i = 0; i < 256; i++) {
compress_dictionary[string(1, i)] = i;
}
string current_string;
unsigned int code;
unsigned int next_code = 256;
//Output file for compressed data
ofstream outputFile;
outputFile.open(filename + ".lzw");
for (char& c : input) {
current_string = current_string + c;
if (compress_dictionary.find(current_string) == compress_dictionary.end()) {
if (next_code <= MAX_DEF)
compress_dictionary.insert(make_pair(current_string, next_code++));
current_string.erase(current_string.size() - 1);
outputFile << convert_int_to_bin(compress_dictionary[current_string]);
current_string = c;
}
}
if (current_string.size())
outputFile << convert_int_to_bin(compress_dictionary[current_string]);
outputFile.close();
}
The results of the compression from:
Parallelizing
We did not see any other way to parallelize the algorithm.
Assignment 2
In order to parallelize the code from above, we decided to use a kernel to handle the calculations.
The logic largely remains the same, but we offload the CPU calculations to the GPU.
This code generates random points within the kernel and the calculations are also done in here.
Offloading to the GPU results in a pi calculation time to be reduced
Kernel code used
__global__ void calculate(float *d_pi, curandState *states, float n) {
unsigned int tid = threadIdx.x + blockDim.x * blockIdx.x;
float points = 0;
float x, y;
curand_init(1000, tid, 0, &states[tid]); // Initialize CURAND
for (int i = 0; i < n; i++) {
x = curand_uniform(&states[tid]); //calls random float from 0.0 to 1.0
y = curand_uniform(&states[tid]);
points += (x*x + y*y <= 1.0f); // count if x & y is in the circle.
}
d_pi[tid] = 4.0f * points / n; // return estimate of pi
}
cuRAND documentation.
Results CPU vs GPU
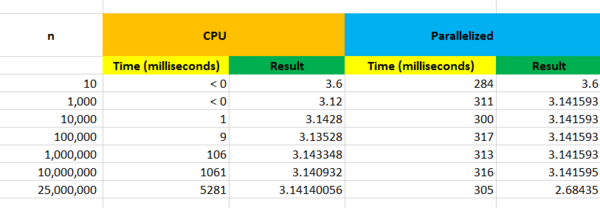
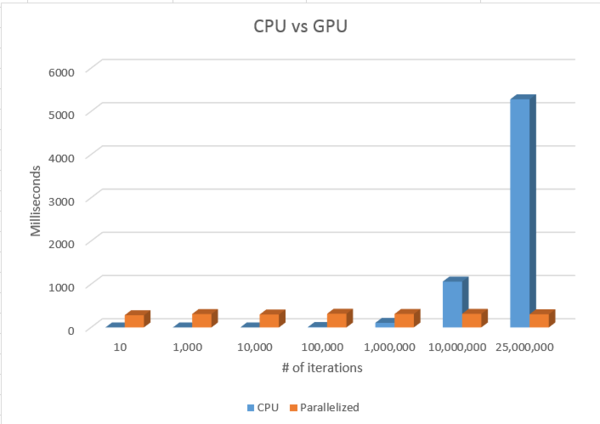
As we can see above, the more iterations, the more accurate the calculation of PI.
The CPU's results drastically change as we increase the iteration 10x.
However, the parallelized results seem to stay accurate throughout the iterations.
It seems as though the calculation time doesn't change much and stays consistent.
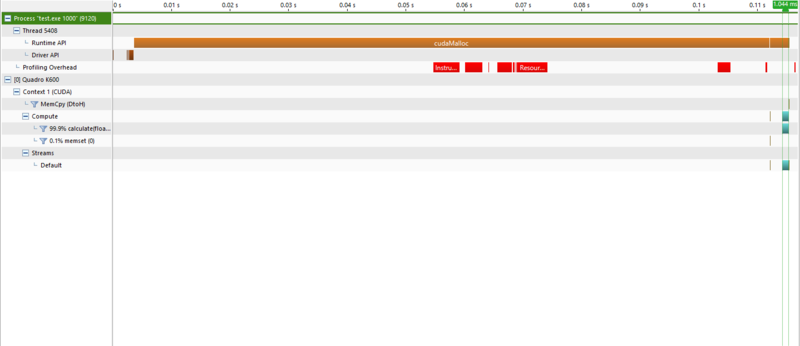
Profiling the code shows that cudaMalloc takes up most of the time spent. Even when
there are 10 iterations, the time remains at 300 milliseconds.
As the iteration passes 25 million, we have a bit of memory leak which results in inaccurate results.
In order to optimize the code, we must find a way reduce the time cudaMalloc takes.
Assignment 3
After realizing the cudaMemcpy and cudaMalloc takes quite a bit of time, we focused our efforts on optimizing it.
It was difficult to find a solution because the initial copy takes a bit of time to set up.
We tried using cudaMallocHost to see if we can allocate memory instead of using malloc.
cudaMallocHost will allocate pinned memory which is stored in RAM and can be accessed by the GPU's DMA directly.
We changed one part of our code
cudaMallocHost((void **)&host, size);
Here we can see where an error occurs, we suspect that a memory leak causes the problem resulting in an error in pi calculation
The final results show that although cudaMallocHost should imporve the speed of memory transfer, if didn't make much
of a difference here. In conclusion, we can see that the GPU performance is significantly faster than the CPU's performance.