Difference between revisions of "GPU610/Turing"
(→Assignment 1) |
(→Assignment 3) |
||
| (58 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
= Team Turing = | = Team Turing = | ||
== Team Members == | == Team Members == | ||
| − | # [mailto:cjcampbell2@myseneca.ca?subject=gpu610 Colin Campbell] | + | # [mailto:cjcampbell2@myseneca.ca?subject=gpu610 Colin Campbell] |
| − | |||
| − | |||
| − | [mailto:cjcampbell2 | + | [mailto:cjcampbell2@myseneca.ca?subject=dps901-gpu610 Email All] |
== Progress == | == Progress == | ||
| Line 19: | Line 17: | ||
The program accepts a single number to specify the size of a square matrix and runs the equation 100 times. When run with a 10000x10000 matrix this is the result: | The program accepts a single number to specify the size of a square matrix and runs the equation 100 times. When run with a 10000x10000 matrix this is the result: | ||
[[Image:GPU610_Turing_A1Profile_10k.jpg|600px]] | [[Image:GPU610_Turing_A1Profile_10k.jpg|600px]] | ||
| + | |||
| + | Running a 10000 x 10000 matrix through 100 time steps takes just over 1 minute. 82.5% of the process time is spent in the evolveTimeStep function, which takes approx 600ms per time step. The timeStep function has a nested for loop giving it a O(N^2) runtime. With a 20000 x 20000 matrix each step takes approx. 2200ms on my machine. I cannot accurately benchmark above this size on my machine as the process requires more memory than my computer has. | ||
===== Potential for parallelism ===== | ===== Potential for parallelism ===== | ||
| Line 24: | Line 24: | ||
This is the function that takes most of the time. As you can see it it a single nested for loop that calculates a value from Matrix ui and stores it in Matrix u. Because the first matrix is never changed in each step, the result can therefore be calculated in independent threads safely. this means that this code should be relatively simple to parallelize and should see large speed increases. | This is the function that takes most of the time. As you can see it it a single nested for loop that calculates a value from Matrix ui and stores it in Matrix u. Because the first matrix is never changed in each step, the result can therefore be calculated in independent threads safely. this means that this code should be relatively simple to parallelize and should see large speed increases. | ||
| + | |||
| + | ==== James's Research ==== | ||
| + | An image processing code was found here: http://www.dreamincode.net/forums/topic/76816-image-processing-tutorial/ | ||
| + | This program takes in an image and processes in various ways. I chose to look at the reflection function (flipping) by editing the code to omit the other sections. Below are the results from profiling where n is the size of the image in bytes. | ||
| + | |||
| + | |||
| + | |||
| + | {| cellspacing="0" border="0" | ||
| + | | align="right" | n | ||
| + | | align="center" | writeImage(char*, Image&) | ||
| + | | align="center" | readImage(char*, Image&) | ||
| + | | align="center" | Image::reflectImage(bool, Image&) | ||
| + | | Image::Image(int, int, int) | ||
| + | | align="center" | Image::operator=(Image const&) | ||
| + | | align="center" | Image::Image(Image const&) | ||
| + | | Elapsed Time | ||
| + | |- | ||
| + | | align="right" | 10077713 | ||
| + | | align="right" | 0.01 | ||
| + | | align="right" | 0.01 | ||
| + | | align="right" | 0.02 | ||
| + | | align="right" | 0.01 | ||
| + | | align="right" | 0.01 | ||
| + | | align="right" | 0.07 | ||
| + | | align="right" | 0.11 | ||
| + | |- | ||
| + | | align="right" | 25435697 | ||
| + | | align="right" | 0.02 | ||
| + | | align="right" | 0.02 | ||
| + | | align="right" | 0.03 | ||
| + | | align="right" | 0.05 | ||
| + | | align="right" | 0.05 | ||
| + | | align="right" | 0.09 | ||
| + | | align="right" | 0.26 | ||
| + | |- | ||
| + | | align="right" | 117430458 | ||
| + | | align="right" | 0.13 | ||
| + | | align="right" | 0.1 | ||
| + | | align="right" | 0.15 | ||
| + | | align="right" | 0.18 | ||
| + | | align="right" | 0.2 | ||
| + | | align="right" | 0.6 | ||
| + | | align="right" | 1.36 | ||
| + | |} | ||
| + | |||
| + | What takes the longest is the function that copies the old image into the new output image. Below is the code for the function. | ||
| + | |||
| + | Image::Image(const Image& oldImage) | ||
| + | { | ||
| + | N = oldImage.N; | ||
| + | M = oldImage.M; | ||
| + | Q = oldImage.Q; | ||
| + | |||
| + | pixelVal = new int* [N]; | ||
| + | for(int i = 0; i < N; i++) | ||
| + | { | ||
| + | pixelVal[i] = new int [M]; | ||
| + | for(int j = 0; j < M; j++) | ||
| + | pixelVal[i][j] = oldImage.pixelVal[i][j]; | ||
| + | } | ||
| + | } | ||
| + | I believe there is potential at possibly parallelizing the nested for loop. | ||
| + | ==== Chadd's Research ==== | ||
| + | Data Decomposition is involves the dividing to a Large chunk a of Data into smaller sections of data. A processes is | ||
| + | then preformed on the smaller pieces of data until the entire chunk of data is processed or the programs end because | ||
| + | it has reached its goal. | ||
| + | |||
| + | ==== Chadd's Example ==== | ||
| + | [[Image:Data Decomp.png|600px ]] | ||
| + | |||
| + | I choose one of the most common application of data decomposition :File Search. I created a program that accepts a file and searches it for a specific word entered by | ||
| + | the user. The program also counts the number of lines in the file and the number of matches found in the file. | ||
| + | |||
| + | ==== Potential for parallelism ==== | ||
| + | |||
| + | [[Image:loop.png|600px ]] | ||
| + | |||
| + | |||
| + | |||
| + | I think by making the nested loop above parallel I should be able to | ||
| + | produce a more efficient program. This section of the code uses a | ||
| + | majority of the CPU's power. This is where the program is actually | ||
| + | though the file line by line and then word by word. Profiling data | ||
| + | is available below. | ||
| + | |||
| + | [[Image:profile2.png|600px ]] | ||
| + | |||
| + | |||
| + | ==== Conclusion ==== | ||
| + | We have decided to use the diffusion equation code for assignment 2 because it uses simple matrixes, making it a good candidate for parallelism. | ||
=== Assignment 2 === | === Assignment 2 === | ||
| + | ==== Colin's Report ==== | ||
| + | For assignment 2 we chose the Heat Equation problem. I profiled both the serial and CUDA versions of the code by taking the average of 25 steps in milliseconds. | ||
| + | |||
| + | The tests were run on a laptop with a GeForce 650 GPU. Due to memory constraints the maximum size of the matrix that could be run was 15000x15000. | ||
| + | |||
| + | I've created a chart comparing the runtimes | ||
| + | |||
| + | [[Image:GPUA2Colin.png|400px]] | ||
| + | |||
| + | ====== Conclusions ====== | ||
| + | There were no major issues converting the code to CUDA as it's a simple matrix, which made it very straightforward. When I first converted the code I did however notice that it was running slower than the CPU version. This was caused by inefficient block sizing. I managed to fix it by modifying the number of threads per block until it made more efficient use of the CUDA cores. In the end, without any other optimizations it runs at around twice the speed of the CPU code. | ||
| + | |||
| + | ==== Chadd's Findings ==== | ||
| + | Profiling the Diffusion Equation I noticed that the majority of the time is spent in the Evolvetimestep function. | ||
| + | Using my home computer with a GTX 560 ti Nvidia graphics card I ran a matrix 9000x9000 10 times. I have the runtime results in the chart below. | ||
| + | |||
| + | I've created a chart comparing the runtimes | ||
| + | |||
| + | [[Image:Runtime.png|400px]] | ||
| + | |||
| + | |||
| + | I used 32 threads per block size in my paralellization of the nested for loop found in the Evolvetimestep function. The results were very good. | ||
| + | |||
=== Assignment 3 === | === Assignment 3 === | ||
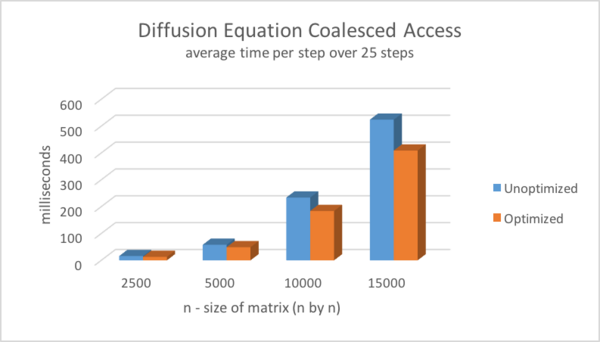
| + | The first optimization I was able to make was using thread coalescence. This lead to a moderate per step speedup as seen in this graph. | ||
| + | |||
| + | [[Image:ColinCampbellGPU610A3G1.png|600px| ]] | ||
| + | |||
| + | I then attempted to modify the code to use shared memory. Unfortunately the way the algorithm accesses rows and columns out of order made this not viable. I tried to convert the problem to use tiling to get around this but was not able to make it work correctly. Because of this I was not able to implement any more optimizations as most were based around using shared memory efficiently. | ||
Latest revision as of 11:58, 13 December 2015
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
Team Turing
Team Members
Progress
Assignment 1
For assignment 1 we each looked at a different application to profile. Colin profiled a 2d Diffusion equation program. Chaddwick profiled data decomposition and James profiled an image manipulation function.
Colin's Findings
I found a python script located at http://www.timteatro.net/2010/10/29/performance-python-solving-the-2d-diffusion-equation-with-numpy/ that uses a nested For Loop to calculate the diffusion equation. I translated the script into C++ and profiled it using XCode's native profiler.
Example
The program accepts a single number to specify the size of a square matrix and runs the equation 100 times. When run with a 10000x10000 matrix this is the result:
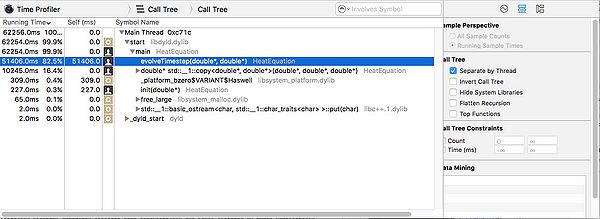
Running a 10000 x 10000 matrix through 100 time steps takes just over 1 minute. 82.5% of the process time is spent in the evolveTimeStep function, which takes approx 600ms per time step. The timeStep function has a nested for loop giving it a O(N^2) runtime. With a 20000 x 20000 matrix each step takes approx. 2200ms on my machine. I cannot accurately benchmark above this size on my machine as the process requires more memory than my computer has.
Potential for parallelism
This is the function that takes most of the time. As you can see it it a single nested for loop that calculates a value from Matrix ui and stores it in Matrix u. Because the first matrix is never changed in each step, the result can therefore be calculated in independent threads safely. this means that this code should be relatively simple to parallelize and should see large speed increases.
James's Research
An image processing code was found here: http://www.dreamincode.net/forums/topic/76816-image-processing-tutorial/ This program takes in an image and processes in various ways. I chose to look at the reflection function (flipping) by editing the code to omit the other sections. Below are the results from profiling where n is the size of the image in bytes.
| n | writeImage(char*, Image&) | readImage(char*, Image&) | Image::reflectImage(bool, Image&) | Image::Image(int, int, int) | Image::operator=(Image const&) | Image::Image(Image const&) | Elapsed Time |
| 10077713 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.07 | 0.11 |
| 25435697 | 0.02 | 0.02 | 0.03 | 0.05 | 0.05 | 0.09 | 0.26 |
| 117430458 | 0.13 | 0.1 | 0.15 | 0.18 | 0.2 | 0.6 | 1.36 |
What takes the longest is the function that copies the old image into the new output image. Below is the code for the function.
Image::Image(const Image& oldImage) {
N = oldImage.N;
M = oldImage.M;
Q = oldImage.Q;
pixelVal = new int* [N];
for(int i = 0; i < N; i++)
{
pixelVal[i] = new int [M];
for(int j = 0; j < M; j++)
pixelVal[i][j] = oldImage.pixelVal[i][j];
}
} I believe there is potential at possibly parallelizing the nested for loop.
Chadd's Research
Data Decomposition is involves the dividing to a Large chunk a of Data into smaller sections of data. A processes is then preformed on the smaller pieces of data until the entire chunk of data is processed or the programs end because it has reached its goal.
Chadd's Example
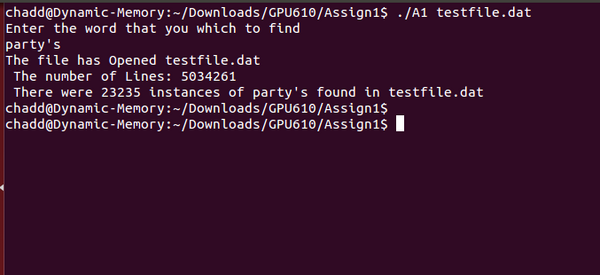
I choose one of the most common application of data decomposition :File Search. I created a program that accepts a file and searches it for a specific word entered by the user. The program also counts the number of lines in the file and the number of matches found in the file.
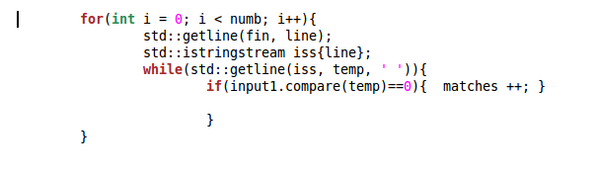
Potential for parallelism
I think by making the nested loop above parallel I should be able to produce a more efficient program. This section of the code uses a majority of the CPU's power. This is where the program is actually though the file line by line and then word by word. Profiling data is available below.
Conclusion
We have decided to use the diffusion equation code for assignment 2 because it uses simple matrixes, making it a good candidate for parallelism.
Assignment 2
Colin's Report
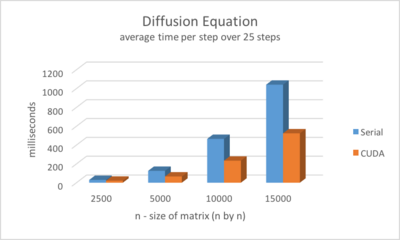
For assignment 2 we chose the Heat Equation problem. I profiled both the serial and CUDA versions of the code by taking the average of 25 steps in milliseconds.
The tests were run on a laptop with a GeForce 650 GPU. Due to memory constraints the maximum size of the matrix that could be run was 15000x15000.
I've created a chart comparing the runtimes
Conclusions
There were no major issues converting the code to CUDA as it's a simple matrix, which made it very straightforward. When I first converted the code I did however notice that it was running slower than the CPU version. This was caused by inefficient block sizing. I managed to fix it by modifying the number of threads per block until it made more efficient use of the CUDA cores. In the end, without any other optimizations it runs at around twice the speed of the CPU code.
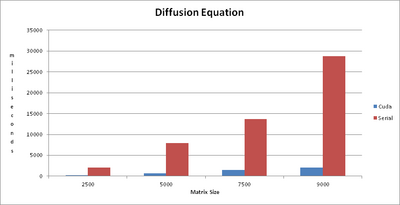
Chadd's Findings
Profiling the Diffusion Equation I noticed that the majority of the time is spent in the Evolvetimestep function. Using my home computer with a GTX 560 ti Nvidia graphics card I ran a matrix 9000x9000 10 times. I have the runtime results in the chart below.
I've created a chart comparing the runtimes
I used 32 threads per block size in my paralellization of the nested for loop found in the Evolvetimestep function. The results were very good.
Assignment 3
The first optimization I was able to make was using thread coalescence. This lead to a moderate per step speedup as seen in this graph.
I then attempted to modify the code to use shared memory. Unfortunately the way the algorithm accesses rows and columns out of order made this not viable. I tried to convert the problem to use tiling to get around this but was not able to make it work correctly. Because of this I was not able to implement any more optimizations as most were based around using shared memory efficiently.