Difference between revisions of "GPU621/MKL"
(→How MKL Improves Efficiency) |
(→What is Math Kernel Library?) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 4: | Line 4: | ||
== Overview == | == Overview == | ||
| − | This project aims to explore the Intel Math Kernel Library and find out how it functions, its efficiency, as well as its advantages and disadvantages when | + | This project aims to explore the Intel Math Kernel Library and find out how it functions, its efficiency, as well as its advantages and disadvantages when utilized in the real world. This will be accomplished through an examination of how to include and apply Math Kernel Library functionality to a program, and the resulting effect on computational efficiency. |
| − | + | == What is Math Kernel Library == | |
| − | == What is Math Kernel Library | ||
Released on May 9, 2003, Intel's oneAPI Math Kernel Library, also known as Intel oneMKL or Intel MKL, is a library tailored towards the optimization of numerical computation in the fields such as science, engineering and finance. MKL functions by parallelizing computation routines processing on both the CPU and GPU. The library provides functionality improvements for calculations including: | Released on May 9, 2003, Intel's oneAPI Math Kernel Library, also known as Intel oneMKL or Intel MKL, is a library tailored towards the optimization of numerical computation in the fields such as science, engineering and finance. MKL functions by parallelizing computation routines processing on both the CPU and GPU. The library provides functionality improvements for calculations including: | ||
Latest revision as of 15:45, 30 November 2022
Contents
- 1 Intel Math Kernel Library
- 1.1 Overview
- 1.2 What is Math Kernel Library
- 1.3 Installation/Setup
- 1.4 Effectiveness of MKL in Matrix Multiplication
- 1.5 Matrix Multiplication Comparison Source Code
- 1.6 How MKL Improves Efficiency
- 1.7 Other Mathematical Functionality
- 1.8 Advantages
- 1.9 Disadvantages
- 1.10 Conclusion
- 1.11 References
Intel Math Kernel Library
Overview
This project aims to explore the Intel Math Kernel Library and find out how it functions, its efficiency, as well as its advantages and disadvantages when utilized in the real world. This will be accomplished through an examination of how to include and apply Math Kernel Library functionality to a program, and the resulting effect on computational efficiency.
What is Math Kernel Library
Released on May 9, 2003, Intel's oneAPI Math Kernel Library, also known as Intel oneMKL or Intel MKL, is a library tailored towards the optimization of numerical computation in the fields such as science, engineering and finance. MKL functions by parallelizing computation routines processing on both the CPU and GPU. The library provides functionality improvements for calculations including:
- Linear algebra
- Fast Fourier transformations
- Vectorization and matrix operations
- Eigenvalue calculations
- Random number generation
MKL has seen use in the real world by handling data sets from a wide range of sources resulting in benefits such as assisting in applying machine learning techniques to large data sets and reducing the usage of energy in office buildings.
Installation/Setup
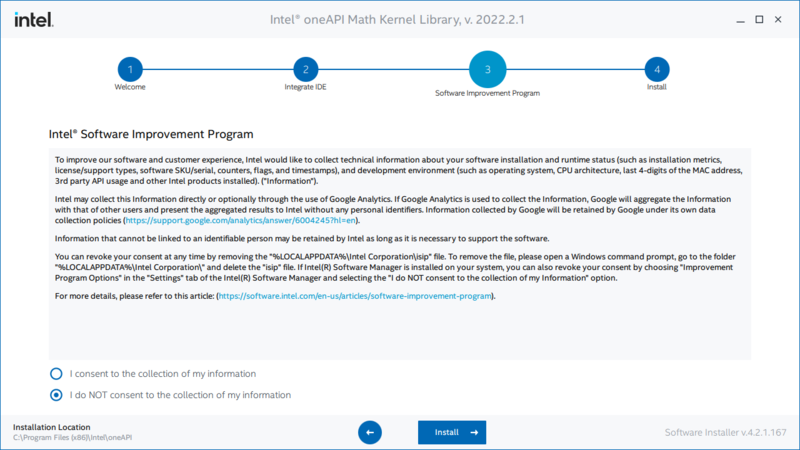
Follow the steps listed below in order to include Math Kernel Library functionality to a program. Alternatively Intel's MKL Get Started Guide can be referenced
In this case we will be using the online installer provided by Intel, support for offline installation and installation via packet managers is also available, for example NuGet Package Manager on Visual Studio.
1. Download MKL
2. Open installer
3. Follow installer instructions
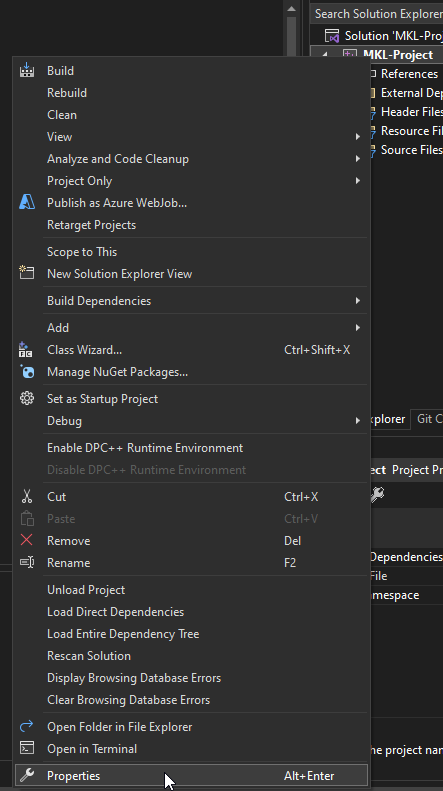
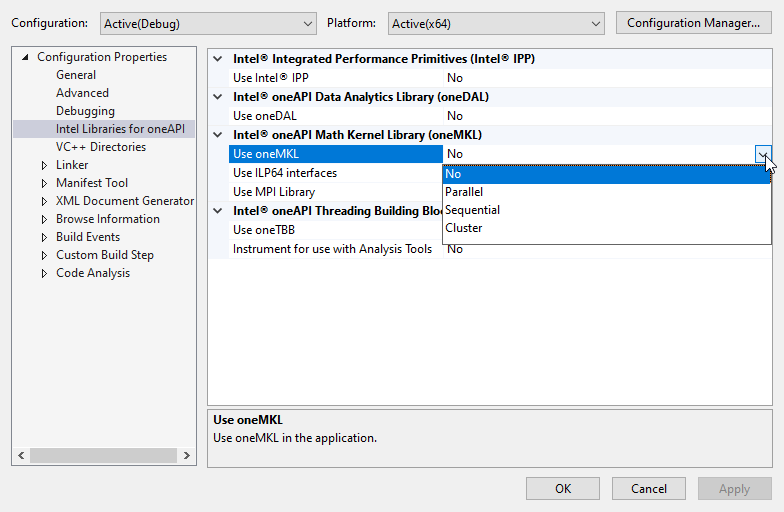
4. Access project properties in Visual Studio
5. Enable usage of MKL
6. Include MKL header file "mkl.h"
Installing and compiling on Linux or macOS may require additional steps such as linking code.
Effectiveness of MKL in Matrix Multiplication
To determine the effectiveness of Math Kernel Library functionality, a comparison using matrix multiplication will be done to see the difference between unoptimized computation and computation using MKL. The source code for both sets of calculations are presented below.
Matrix Multiplication without MKL Optimization (nested loops)
printf (" Making the first run of matrix product using triple nested loop\n"
" to get stable run time measurements \n\n");
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
printf (" Measuring performance of matrix product using triple nested loop \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
}
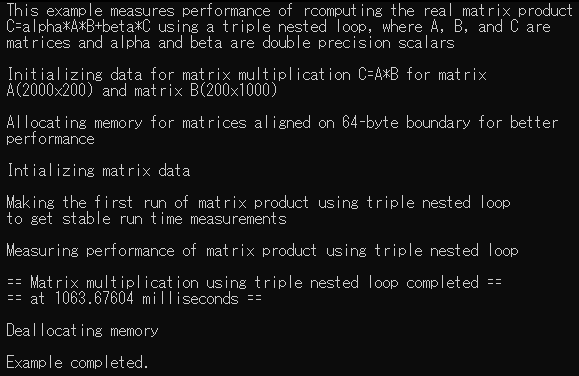
Result of Unoptimized Matrix Multiplication (using nested loops)
Matrix Multiplication with MKL Optimization (cblas_dgemm())
printf(" Making the first run of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface to get stable run time measurements \n\n");
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
printf(" Measuring performance of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
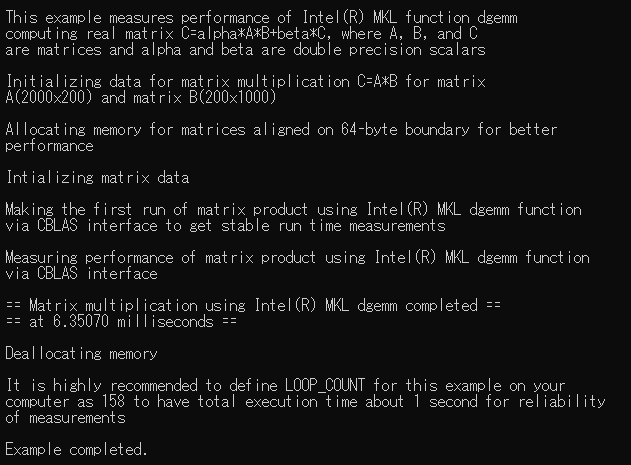
Result of Optimized Matrix Multiplication (using cblas_dgemm())
In this case, the effects of using MKL functionality can be clearly seen in a noticeable 167x increase in computation speed between the unoptimized and optimized calculations. While the proportional increase in performance may not always be so drastic, the difference in performance by using MKL extends both towards smaller and larger scales.
Matrix Multiplication Comparison Source Code
Full Source Code for Unoptimized Calculation
#define min(x,y) (((x) < (y)) ? (x) : (y))
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
/* Consider adjusting LOOP_COUNT based on the performance of your computer */
/* to make sure that total run time is at least 1 second */
#define LOOP_COUNT 10
int main()
{
double *A, *B, *C;
int m, n, p, i, j, k, r;
double alpha, beta;
double sum;
double s_initial, s_elapsed;
printf ("\n This example measures performance of rcomputing the real matrix product \n"
" C=alpha*A*B+beta*C using a triple nested loop, where A, B, and C are \n"
" matrices and alpha and beta are double precision scalars \n\n");
m = 2000, p = 200, n = 1000;
printf (" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf (" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double *)mkl_malloc( m*p*sizeof( double ), 64 );
B = (double *)mkl_malloc( p*n*sizeof( double ), 64 );
C = (double *)mkl_malloc( m*n*sizeof( double ), 64 );
if (A == NULL || B == NULL || C == NULL) {
printf( "\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf (" Intializing matrix data \n\n");
for (i = 0; i < (m*p); i++) {
A[i] = (double)(i+1);
}
for (i = 0; i < (p*n); i++) {
B[i] = (double)(-i-1);
}
for (i = 0; i < (m*n); i++) {
C[i] = 0.0;
}
printf (" Making the first run of matrix product using triple nested loop\n"
" to get stable run time measurements \n\n");
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
printf (" Measuring performance of matrix product using triple nested loop \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p*i+k] * B[n*k+j];
C[n*i+j] = sum;
}
}
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf (" == Matrix multiplication using triple nested loop completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
printf (" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
if (s_elapsed < 0.9/LOOP_COUNT) {
s_elapsed=1.0/LOOP_COUNT/s_elapsed;
i=(int)(s_elapsed*LOOP_COUNT)+1;
printf(" It is highly recommended to define LOOP_COUNT for this example on your \n"
" computer as %i to have total execution time about 1 second for reliability \n"
" of measurements\n\n", i);
}
printf (" Example completed. \n\n");
return 0;
}
Full Source Code for Optimized Calculations
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
/* Consider adjusting LOOP_COUNT based on the performance of your computer */
/* to make sure that total run time is at least 1 second */
#define LOOP_COUNT 10
int main()
{
double* A, * B, * C;
int m, n, p, i, r;
double alpha, beta;
double s_initial, s_elapsed;
printf("\n This example measures performance of Intel(R) MKL function dgemm \n"
" computing real matrix C=alpha*A*B+beta*C, where A, B, and C \n"
" are matrices and alpha and beta are double precision scalars\n\n");
m = 2000, p = 200, n = 1000;
printf(" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf(" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double*)mkl_malloc(m * p * sizeof(double), 64);
B = (double*)mkl_malloc(p * n * sizeof(double), 64);
C = (double*)mkl_malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) {
printf("\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf(" Intializing matrix data \n\n");
for (i = 0; i < (m * p); i++) {
A[i] = (double)(i + 1);
}
for (i = 0; i < (p * n); i++) {
B[i] = (double)(-i - 1);
}
for (i = 0; i < (m * n); i++) {
C[i] = 0.0;
}
printf(" Making the first run of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface to get stable run time measurements \n\n");
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
printf(" Measuring performance of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf(" == Matrix multiplication using Intel(R) MKL dgemm completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
printf(" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
if (s_elapsed < 0.9 / LOOP_COUNT) {
s_elapsed = 1.0 / LOOP_COUNT / s_elapsed;
i = (int)(s_elapsed * LOOP_COUNT) + 1;
printf(" It is highly recommended to define LOOP_COUNT for this example on your \n"
" computer as %i to have total execution time about 1 second for reliability \n"
" of measurements\n\n", i);
}
printf(" Example completed. \n\n");
return 0;
}
How MKL Improves Efficiency
In this instance the MKL used DGEMM to improve the calculation time. DGEMM stands for Double-precision, GEneral Matrix-Matrix multiplication. In the example used to demonstrate matrix multiplication, the code defines the multiplication of two matrices along with scaling factors alpha and beta. It can be noted that without MKL implementation the matrix multiplication is done though nested loops, however in the MKL optimized version cblas_dgemm() is called. The dgemm refers to DGEMM defined above and cblas refers to the CBLAS interface, which stands for Basic Linear Algebra Subprograms in C.
One part of BLAS, level 3, is dedicated to matrix-matrix operations, which in this case includes the matrix multiplication calculations. While the math and logic behind the implementation of the cblas_dgemm() function is fairly complicated, a simplified explanation on how it works can be expressed as the decomposition of either one or both of the matrices being multiplied and taking advantage of cache memory to improve computation speed. The decomposition of matrices into block matrices allows for general matrix-matrix multiplication to be conducted recursively. By using a beta parameter with the block matrices a multiplication calculation can be eliminated from each member of the resulting matrix
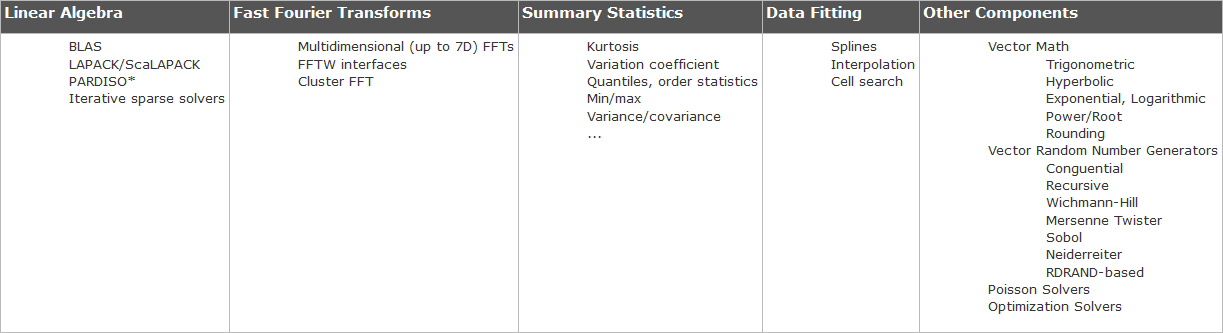
Other Mathematical Functionality
While the example used to explore the effectiveness of MKL utilizes matrix multiplication, the library provides functionality in a variety of other mathematical categories.
Some notable functionality provided in the Math Kernel Library include the following.
Basic Linear Algebra Subprograms (BLAS):
− level 1 BLAS: vector operations
− level 2 BLAS: matrix-vector operations
− level 3 BLAS: matrix-matrix operations
Sparse BLAS Level 1, 2, and 3: Basic operations on sparse vectors and matrices
LAPACK^2: Linear equations, least square problems, eigenvalues
ScaLAPACK^3: Computational, driver, and auxiliary routines for solving systems of linear equations across a compute cluster
PBLAS: Distributed vector, matrix-vector, and matrix-matrix operations
General and Cluster Fast Fourier Transform functions: Computation of Discrete Fourier Transformations and FFT across complete clusters
Solver Routines: Non linear least squares through Trust-Region algorithms
Data Fitting: Spline based approximation functions, derivatives, integrals and cell search
Advantages
- Wide variety of functions
- Highly optimized computation algorithms
- Wide range of compatibility
- Effective use of parallelization in conjunction with hardware
Disadvantages
- Requires standalone installation and implementation
- Mathematical knowledge can be highly beneficial to efficient usage of library functionality
- Poor(er) compatibility and efficiency on AMD hardware
Conclusion
Intel Math Kernel Library is a powerful library which can greatly enhance a program's ability to perform mathematical computations. With proper knowledge on how to effectively utilize MKL functionality, the overall efficiency of the program can be drastically improved. Usage of MKL has already yielded real world results in a variety of fields, and will continue to do so as the scope of programs, data and the issues they tackle increases.
References
https://www.sciencedirect.com/topics/computer-science/intel-math-kernel-library