GPU621/False Sharing

Analyzing False Sharing

Group Members

- Kevin Chou

Introduction

False sharing is a well-known problem that can occur when taking advantage of parallelization in modern multi-processor computers with shared memory. Although the results will be correct, frequent false sharing results in significant performance loss and reduction in scalability, effectively nullifying the benefits of parallel computing.

The Cache

What is a Cache?

Before we can talk about false sharing, we need a brief overview of a cache. Like other storage mediums, a cache is a place used to store data and instructions that the CPU may use.

So why do we have so many types?

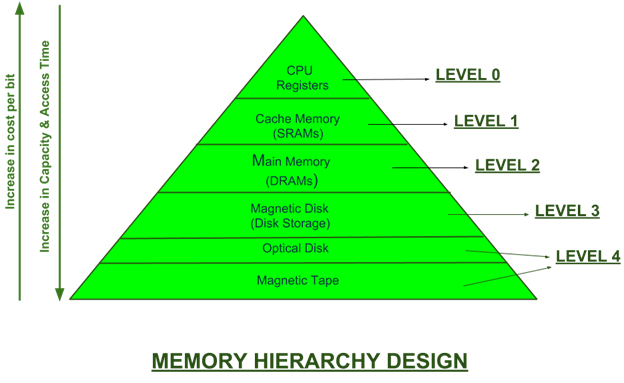
In an ideal world, the CPU would have lightning-fast access to all the data on your machine at any given time to maximize the speed and power of modern-day CPUs. In reality, there are limitations and trade-offs when balancing speed, storage size, location, and cost. To compromise, a computer utilizes many types of memory. To name the major ones in the hierarchy, we have secondary memory like hard drives and SSDs which can permanently hold vast quantities of data but are slow. Next is Dynamic Random Access Memory(DRAM) which is much smaller, faster, and volatile. Last, we have the cache or Static Random Access Memory(SRAM), which is extremely fast, but even smaller and more expensive. If the CPU solely relied on getting data from secondary memory, the slow access speed of the storage device would become a massive bottleneck in computation time. There would be huge gaps of time where the CPU sits around doing nothing waiting for data. To the end user, your machine would appear to be extremely sluggish and non-responsive.

At the same time, only small amounts piece of data is needed at any given moment. Even if you brought everything in from memory, most of it will be unused. Using the different types of memory storage, the most relevant data can be siphoned from secondary memory ahead of time and stored in the cache and RAM. When searching for that data, the CPU can grab it from the cache (cache hit). If it is not there (cache miss), then it looks in RAM and then secondary memory. By minimizing the number of cache misses, this ensures the CPU has a steady flow of data it can quickly retrieve and compute.

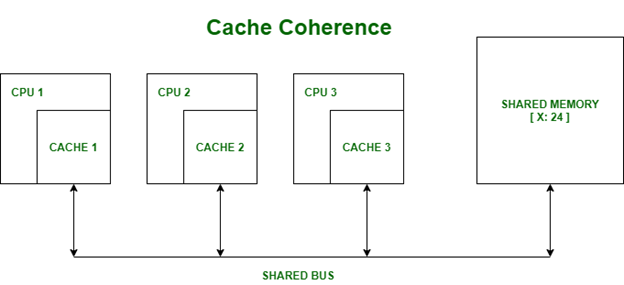
Cache Coherence and Cache Line

Each processor has their own local cache. When data is needed, a fixed block of memory is transferred to the cache; this block is known as a cache line.

However, if they each modify their own copy, how do we know which one correct?

We can’t store all the different versions of the data and or just pick a random one to be the correct version, this would create havoc in our computer systems. The answer is we need cache coherence which is the uniformity of shared resource data that ends up stored in multiple local caches. In other words, we must keep all the local caches synchronized. The challenge of doing so is known as the Cache Coherence Problem. To solve this problem, multiprocessor systems rely on coherence protocols to manage and maintain cache coherency.

False Sharing

What is False Sharing?

Now that we understand the basics of a cache, how does this relate to the concept of false sharing?

False sharing occurs when multiple processors modify data that resides on the same cache line. When this data is written back to memory, the shared cache lines are marked as invalid or dirty. Processors must fetch an updated copy introducing significant delays due to memory access speeds. As you increase the number of processors, this quickly spirals out of control as there is an increasing chance the cache line is invalid.

The key thing to note is that you do not need to modify the same piece of data. If the modified data happens to belong to the same cache line, the cache will be invalidated, forcing a memory update to maintain cache coherency.

Analyzing Workshop Example

#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <chrono>
#include <omp.h>

#define NUM_THREADS 8

using namespace std::chrono;

// report system time
void reportTime(const char* msg, steady_clock::duration span)
{
    auto ms = duration_cast<milliseconds>(span);
    std::cout << msg << " - took - " <<
        ms.count() << " milliseconds" << std::endl;
}

int main(int argc, char** argv)
{
    if (argc != 2)
    {
        std::cerr << argv[0] << ": invalid number of arguments\n";
        std::cerr << "Usage: " << argv[0] << "  no_of_slices\n";
        return 1;
    }
    int n = std::atoi(argv[1]);
    steady_clock::time_point ts, te;

    // calculate pi by integrating the area under 1/(1 + x^2) in n steps
    ts = steady_clock::now();

    int actual_thread_count;
    double pi = 0.0f;
    double sum[NUM_THREADS] = { 0.0f };
    double step = 1.0 / (double)n;

    omp_set_num_threads(NUM_THREADS);
    #pragma omp parallel
    {
        int id, num_threads;
        double x;

        id = omp_get_thread_num();
        num_threads = omp_get_num_threads();

        // get master thread to return how many threads were actually created
        if (id == 0)
        {
            actual_thread_count = num_threads;
        }

        // each thread is responsible for calculating the area of a specific set of sections underneath the curve
        for (int i = id; i < n; i = i + num_threads)
        {
            x = ((double)i + 0.5f) * step;
            sum[id] += 1.0f / (1.0f + x * x);
        }
    }

    // sum up each calculation to get approximation of pi
    for (int i = 0; i < actual_thread_count; i++)
    {
        pi += 4 * sum[i] * step;
    }

    te = steady_clock::now();

    std::cout << "n = " << n <<
        std::fixed << std::setprecision(15) <<
        "\n pi(exact) = " << 3.141592653589793 <<
        "\n pi(calcd) = " << pi << std::endl;
    reportTime("Integration", te - ts);
}