Difference between revisions of "DPS921/OpenACC vs OpenMP Comparison"
m |
(Added professor's comments on GPU computation) |
||
| (27 intermediate revisions by 2 users not shown) | |||
| Line 14: | Line 14: | ||
- Nov 9, 2020: Added project description | - Nov 9, 2020: Added project description | ||
- Nov 13, 2020: Determine content sections to be discussed | - Nov 13, 2020: Determine content sections to be discussed | ||
| + | - Nov 15, 2020: Investigate OpenACC learning material and tools | ||
- Nov 18, 2020: Successful installation of required compiler and compilation of OpenACC code | - Nov 18, 2020: Successful installation of required compiler and compilation of OpenACC code | ||
- Nov 19, 2020: Adding MPI into discussion | - Nov 19, 2020: Adding MPI into discussion | ||
| + | |||
| + | == Important notes (prof's feedback) == | ||
| + | Limitation with GPU computation is that GPU can only handle float precision. When calculating double precision, values need to be broken into floating point precision values, and combined back to double precision. This is one of the primary reasons why GPUs are not used in scientific computations. | ||
| + | |||
| + | Before using GPU to speed up computation, make sure you know the level of precision required for the results and intermediate results. For AI/CV/ML where precision requirement is low, it is safe to use GPU to speed up your computation. | ||
= OpenACC = | = OpenACC = | ||
| + | |||
| + | == GPU parallelization vs CPU == | ||
| + | |||
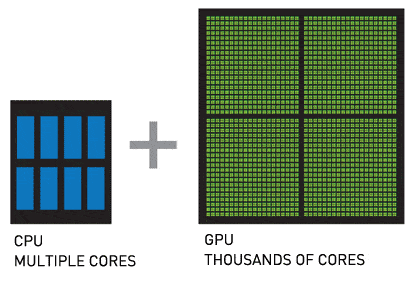
| + | The GPU (Graphics Processing Unit) often consists of thousands of cores, whereas a typical modern multiple core CPU has somewhere between 2 - 128 cores. Even though the GPU cores are smaller than the CPU cores and are much slower at processing serial codes, the high number of cores makes GPUs perform better with parallelized codes in many cases. | ||
| + | |||
| + | [[File:Core-Difference-Between-CPU-and-GPU.gif]] | ||
| + | |||
| + | === Example === | ||
| + | If we want to render a 4k image which has 8.2 million pixels (3,840 x 2,160), we have to do the same rendering algorithm on 8.2 million pixels. The GPU can accomplish this task much more efficient since it has a much higher number of processors that can execute the algorithm at the same time. | ||
== What is OpenACC == | == What is OpenACC == | ||
| − | + | OpenACC (Open Accelerators) is a programming standard for parallel computing on accelerators such as GPUs, which mainly targets Nvidia GPUs. OpenACC is designed to simplify GPU programming, unlike CUDA and OpenCL where you need to write your programs in a different way to achieve GPU acceleration, OpenACC takes a similar approach as OpenMP, which is inserting directives into the code to offload computation onto GPUs and parallelize the code at CUDA core level. It is possible for programmers to create efficient parallel OpenACC code with only minor changes to a serial CPU code. | |
| + | |||
| + | === Benefits of using OpenACC === | ||
| + | * achieve parallelization on GPUs without having to learn an accelerator language such as CUDA | ||
| + | |||
| + | * similar philosophy to OpenMP and very easy to learn | ||
=== Example === | === Example === | ||
| Line 26: | Line 46: | ||
#pragma acc kernels | #pragma acc kernels | ||
{ | { | ||
| − | + | for (int i = 0; i < N; i++) { | |
| − | + | y[i] = a * x[i] + y[i]; | |
| − | + | } | |
} | } | ||
</source> | </source> | ||
| + | For example in this piece of code, the <code>kernels</code> directive tells the compiler that it is up to the compiler to decide how to parallelize the following loop. | ||
| − | == | + | <source> |
| − | [ | + | #pragma acc parallel loop |
| + | { | ||
| + | for (int i = 0; i < N; i++) { | ||
| + | y[i] = a * x[i] + y[i]; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| + | Or if you don't want the compiler to handle everything for you, you can specify there you want this loop to be parallelized, however you as the programmer need to be certain of what you are doing as this will take away some of compiler's freedom of parallelize the code for you. | ||
| − | == | + | == Compiler support == |
Originally, OpenACC compilation is supported by the PGI compiler which requires an expensive subscription, there has been new options in recent years. | Originally, OpenACC compilation is supported by the PGI compiler which requires an expensive subscription, there has been new options in recent years. | ||
| Line 81: | Line 109: | ||
=== GCC[https://gcc.gnu.org/wiki/OpenACC] === | === GCC[https://gcc.gnu.org/wiki/OpenACC] === | ||
| − | + | GCC has added support to OpenACC since GCC 5. The latest GCC version, GCC 10 has support to OpenACC 2.6. | |
| + | To compile OpenACC code with GCC, you need to run | ||
| + | <source> | ||
| + | gcc -fopenacc demo.c | ||
| + | </source> | ||
| + | |||
| + | However, this does not enable any GPU offloading capability. In order to enable GCC with GPU offloading, we need to build some accelerators by ourselves. | ||
| + | |||
| + | For example, to enable GPU offloading on Nvidia GPUs, you need to rebuild GCC with Nvidia PTX, then use the option <code>-foffload=<target></code> to offload generated instructions to accelerator devices. | ||
| + | |||
| + | The instruction of building GCC is over complicated therefore will not be shared here. | ||
= OpenMP vs OpenACC = | = OpenMP vs OpenACC = | ||
| + | |||
| + | [[File:Openaccvsopenmp.png|800px]] | ||
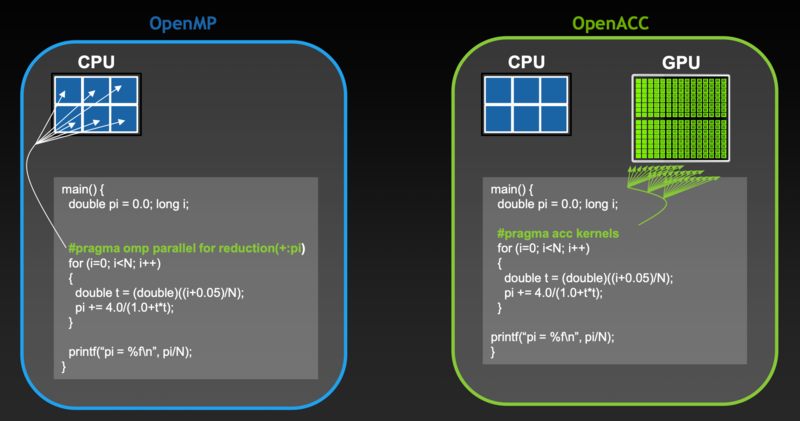
We are comparing with OpenMP for two reasons. First, OpenMP is also based on directives to parallelize code; second, OpenMP started support of offloading to accelerators starting OpenMP 4.0 using <code>target</code> constructs. OpenACC uses directives to tell the compiler where to parallelize loops, and how to manage data between host and accelerator memories. OpenMP takes a more generic approach, it allows programmers to explicitly spread the execution of loops, code regions and tasks across teams of threads. | We are comparing with OpenMP for two reasons. First, OpenMP is also based on directives to parallelize code; second, OpenMP started support of offloading to accelerators starting OpenMP 4.0 using <code>target</code> constructs. OpenACC uses directives to tell the compiler where to parallelize loops, and how to manage data between host and accelerator memories. OpenMP takes a more generic approach, it allows programmers to explicitly spread the execution of loops, code regions and tasks across teams of threads. | ||
| Line 94: | Line 134: | ||
So the real difference between the two is how much freedom is given to the compilers. | So the real difference between the two is how much freedom is given to the compilers. | ||
| − | == | + | |
| + | |||
| + | == Equivalent directives == | ||
'''Explicit conversions''' | '''Explicit conversions''' | ||
| Line 150: | Line 192: | ||
</source> | </source> | ||
| − | '''Copy | + | '''Copy''' |
<source> | <source> | ||
OpenACC OpenMP | OpenACC OpenMP | ||
int x[10],y[10]; int x[10],y[10]; | int x[10],y[10]; int x[10],y[10]; | ||
| − | #pragma acc data copy(x) | + | #pragma acc data copy(x) copy(y) #pragma omp target data map(x,y) |
{ { | { { | ||
... ... | ... ... | ||
| − | #pragma acc kernels copy(x) | + | #pragma acc kernels copy(x) copy(y) #pragma omp target update to(x) |
{ #pragma omp target map(y) | { #pragma omp target map(y) | ||
// Accelerator Code { | // Accelerator Code { | ||
| Line 171: | Line 213: | ||
== Jacobi Iteration == | == Jacobi Iteration == | ||
| + | Jacobi iteration is a common algorithm that iteratively computes the solution based on neighbour values. The following code sample is a serial version of 1D Jacobi iteration. | ||
| + | <source> | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | === OpenMP CPU Implementation === | ||
| + | An OpenMP implementation would look like the following, with shared data and reduction on summation values | ||
| + | <source> | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | #pragma omp parallel | ||
| + | { | ||
| + | #pragma omp for shared(nx, Anew, A) reduction(max:err) | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | #pragma omp for shared(nx, Anew, A) | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | === OpenACC Basic Implementation === | ||
| + | A basic OpenACC implementation looks like this. | ||
| + | <source> | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | #pragma acc parallel loop reduction(max:err) | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | #pragma acc parallel loop | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | Or you can let the compiler handle it by using <code>kernel</code> instead of <code>parallel loop</code>. You will be notified during compilation how the compiler thinks this thing should be parallelized. | ||
| + | <source> | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | #pragma acc kernel | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | #pragma acc kernel | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | === OpenACC Proper Implementation === | ||
| + | The above implementation is actually slower than the serial version, that is due to the fact that there exists data transfer at the end of each iteration. In order to prevent that from happening, we need to copy the data into the accelerator's memory and copy it out when done. | ||
| + | <source> | ||
| + | #pragma acc data copyin(A[0:nx]) copyout(Anew[0:nx]) | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | #pragma acc kernel | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | #pragma acc kernel | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | </source> | ||
| + | In the above code, we added a <code>copyin(list)</code> for the original matrix of values, and <code>copyout(list)</code> for the computed matrix of results. There are other related directives such as <code>copy(list)</code> which is the combination of both <code>copyin(list)</code> and <code>copyout(list)</code>, <code>create(list)</code> for creating a memory region in the accelerator but not copy any data into it, and <code>present(list)</code> which indicates the list is already in the accelerator, which is often used along with <code>create(list)</code> | ||
| + | |||
| + | |||
| + | === OpenMP GPU Basic Implementation === | ||
| + | Here's the OpenMP GPU basic implementation. Almost everything is the same, just need to enclose everything into an <code>omp target</code> region | ||
| + | <source> | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | #pragma omp target | ||
| + | #pragma omp parallel | ||
| + | { | ||
| + | #pragma omp for shared(nx, Anew, A) reduction(max:err) | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | #pragma omp for shared(nx, Anew, A) | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | === OpenMP GPU Proper Implementation === | ||
| + | Similar to OpenACC, the basic is slow because of data transfer issues, but to optimize OpenMP, you need to explicitly tell the thread how to team up and how to distribute. | ||
| + | <source> | ||
| + | #pragma omp target data map(alloc:Anew) map(A) | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | |||
| + | #pragma omp target teams distribute parallel for reduction(max:error) collapse(2) schedule(static,1) | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | |||
| + | #pragma omp target teams distribute parallel for collapse(2) schedule(static,1) | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | |||
| + | === Execution time === | ||
| + | |||
| + | * OpenMP CPU: 1x | ||
| + | * OpenACC Basic: ~2x (twice as slow) | ||
| + | * OpenACC Proper: ~0.14x (7 times faster) | ||
| + | * OpenMP GPU Basic: ~10x (10 times slower) | ||
| + | * OpenMP GPU Proper: ~0.21x (5 times faster) | ||
= Collaboration = | = Collaboration = | ||
== OpenACC with OpenMP == | == OpenACC with OpenMP == | ||
| − | OpenMP and OpenACC can be used together | + | OpenMP and OpenACC can be used together. Using the example above, we can easily come up with something like |
| + | |||
| + | <source> | ||
| + | #pragma acc data copyin(A[0:nx]) copyout(Anew[0:nx]) | ||
| + | while ( err > tol && iter < iter_max ) { | ||
| + | err=0.0f; | ||
| + | #pragma omp parallel for shared(nx, Anew, A) | ||
| + | #pragma acc kernel | ||
| + | for(int i = 1; i < nx-1; i++) { | ||
| + | Anew[i] = 0.5f * (A[i+1] + A[i-1]); | ||
| + | err = fmax(err, fabs(Anew[i] - A[i])); | ||
| + | } | ||
| + | #pragma omp parallel for shared(nx, Anew, A) | ||
| + | #pragma acc kernel | ||
| + | for( int i = 1; i < nx-1; i++ ) { | ||
| + | A[i] = Anew[i]; | ||
| + | } | ||
| + | iter++; | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | this way, for each thread created by OpenMP, the computation will be offloaded to an accelerator, with results joined back together. | ||
| + | |||
| + | Combining OpenACC and OpenMP together may be an overkill for the 1D example, a 2D example may be a better fit. | ||
| + | <source> | ||
| + | #pragma acc data copy(A), create(Anew) | ||
| + | while ( error > tol && iter < iter_max ) | ||
| + | { | ||
| + | error = 0.f; | ||
| + | |||
| + | #pragma omp parallel for shared(m, n, Anew, A) | ||
| + | #pragma acc kernels loop gang(32), vector(16) | ||
| + | for( int j = 1; j < n-1; j++) | ||
| + | { | ||
| + | #pragma acc loop gang(16), vector(32) | ||
| + | for( int i = 1; i < m-1; i++ ) | ||
| + | { | ||
| + | Anew[j][i] = 0.25f * ( A[j][i+1] + A[j][i-1] | ||
| + | + A[j-1][i] + A[j+1][i]); | ||
| + | error = fmaxf( error, fabsf(Anew[j][i]-A[j][i])); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | #pragma omp parallel for shared(m, n, Anew, A) | ||
| + | #pragma acc kernels loop | ||
| + | for( int j = 1; j < n-1; j++) | ||
| + | { | ||
| + | #pragma acc loop gang(16), vector(32) | ||
| + | for( int i = 1; i < m-1; i++ ) | ||
| + | { | ||
| + | A[j][i] = Anew[j][i]; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | iter++; | ||
| + | } | ||
| + | </source> | ||
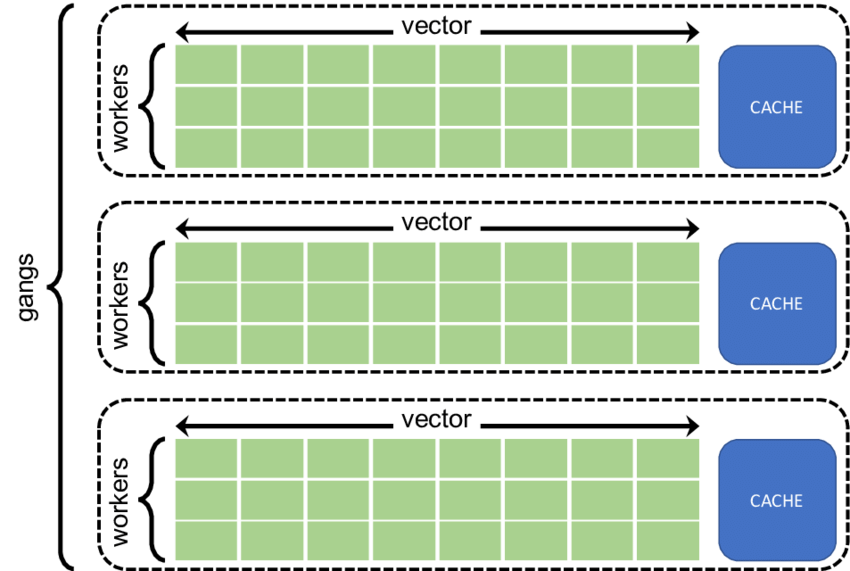
| + | Here we can insert additional instructions into the inner loop on how many gangs and vectors to use. <code>Gang</code> and <code>vector</code> are OpenACC terminologies. A <code>vector</code> is one thread performing single operation on multiple data (SIMD), a <code>worker</code> computes one <code>vector</code>, and a <code>gang</code> comprises of multiple workers that share resource. | ||
| + | |||
| + | [[File: Gangworkervector.png]] | ||
== OpenACC with MPI == | == OpenACC with MPI == | ||
| + | When OpenMP and OpenACC works together, it is usually one CPU with several accelerators as that is how OpenMP works. When there are multiple CPUs and each have access to multiple accelerators, OpenMP will not be enough, and we can introduce MPI. | ||
As we learned that MPI is used to allow communication and data transfer between threads during parallel execution. In the case of multiple accelerators, one of the ways we can use the two together is to use MPI to communicate between different accelerators. | As we learned that MPI is used to allow communication and data transfer between threads during parallel execution. In the case of multiple accelerators, one of the ways we can use the two together is to use MPI to communicate between different accelerators. | ||
| + | |||
| + | The following is a screenshot taken from Nvidia's Advanced OpenACC lecture, showing how does MPI works with OpenACC. | ||
| + | [[File: Mpiopenacc.png|800px]] | ||
| + | |||
| + | = References = | ||
| + | https://developer.nvidia.com/blog/benchmarking-cuda-aware-mpi/ | ||
| + | |||
| + | https://developer.nvidia.com/hpc-sdk | ||
| + | |||
| + | https://gcc.gnu.org/wiki/OpenACC | ||
| + | |||
| + | https://on-demand.gputechconf.com/gtc/2015/webinar/openacc-course/advanced-openacc-techniques.pdf | ||
| + | |||
| + | https://on-demand.gputechconf.com/gtc/2016/presentation/s6510-jeff-larkin-targeting-gpus-openmp.pdf | ||
| + | |||
| + | https://on-demand.gputechconf.com/gtc/2016/webinar/openacc-course/Advanced-OpenACC-Course-Lecture2--Multi-GPU-20160602.pdf | ||
Latest revision as of 18:03, 7 December 2020
Contents
Project Overview
The idea of this project is to introduce OpenACC as a parallel processing library, compare how parallelization is done in different libraries, and identify benefits of using each of the libraries. According to description of both libraries, OpenACC does parallelization more automatically whereas OpenMP allows developers to manually set regions to parallelize and assign to threads. The deliverable of this project would be a introduction to OpenACC along with performance comparison between OpenMP and OpenACC, and a discussion on usage of each one.
Group Members
1. Ruiqi Yu
2. Hanlin Li
3. Le Minh Pham
Progress
- Nov 9, 2020: Added project description - Nov 13, 2020: Determine content sections to be discussed - Nov 15, 2020: Investigate OpenACC learning material and tools - Nov 18, 2020: Successful installation of required compiler and compilation of OpenACC code - Nov 19, 2020: Adding MPI into discussion
Important notes (prof's feedback)
Limitation with GPU computation is that GPU can only handle float precision. When calculating double precision, values need to be broken into floating point precision values, and combined back to double precision. This is one of the primary reasons why GPUs are not used in scientific computations.
Before using GPU to speed up computation, make sure you know the level of precision required for the results and intermediate results. For AI/CV/ML where precision requirement is low, it is safe to use GPU to speed up your computation.
OpenACC
GPU parallelization vs CPU
The GPU (Graphics Processing Unit) often consists of thousands of cores, whereas a typical modern multiple core CPU has somewhere between 2 - 128 cores. Even though the GPU cores are smaller than the CPU cores and are much slower at processing serial codes, the high number of cores makes GPUs perform better with parallelized codes in many cases.
Example
If we want to render a 4k image which has 8.2 million pixels (3,840 x 2,160), we have to do the same rendering algorithm on 8.2 million pixels. The GPU can accomplish this task much more efficient since it has a much higher number of processors that can execute the algorithm at the same time.
What is OpenACC
OpenACC (Open Accelerators) is a programming standard for parallel computing on accelerators such as GPUs, which mainly targets Nvidia GPUs. OpenACC is designed to simplify GPU programming, unlike CUDA and OpenCL where you need to write your programs in a different way to achieve GPU acceleration, OpenACC takes a similar approach as OpenMP, which is inserting directives into the code to offload computation onto GPUs and parallelize the code at CUDA core level. It is possible for programmers to create efficient parallel OpenACC code with only minor changes to a serial CPU code.
Benefits of using OpenACC
- achieve parallelization on GPUs without having to learn an accelerator language such as CUDA
- similar philosophy to OpenMP and very easy to learn
Example
#pragma acc kernels
{
for (int i = 0; i < N; i++) {
y[i] = a * x[i] + y[i];
}
}For example in this piece of code, the kernels directive tells the compiler that it is up to the compiler to decide how to parallelize the following loop.
#pragma acc parallel loop
{
for (int i = 0; i < N; i++) {
y[i] = a * x[i] + y[i];
}
}Or if you don't want the compiler to handle everything for you, you can specify there you want this loop to be parallelized, however you as the programmer need to be certain of what you are doing as this will take away some of compiler's freedom of parallelize the code for you.
Compiler support
Originally, OpenACC compilation is supported by the PGI compiler which requires an expensive subscription, there has been new options in recent years.
Nvidia HPC SDK[1]
Evolved from PGI Compiler community edition. Installation guide are provided in the official website. Currently only supports Linux systems, but Windows support will come soon.
wget https://developer.download.nvidia.com/hpc-sdk/20.9/nvhpc-20-9_20.9_amd64.deb \
https://developer.download.nvidia.com/hpc-sdk/20.9/nvhpc-2020_20.9_amd64.deb
sudo apt-get install ./nvhpc-20-9_20.9_amd64.deb ./nvhpc-2020_20.9_amd64.debAfter installation, the compilers can be found under /opt/nvidia/hpc_sdk/Linux_x86_64/20.9/compilers/bin, and OpenACC code can be compiled with nvc -acc -gpu=manage demo.c, where -acc indicates that the code will include OpenACC directives, and -gpu=manage indicates how should memory be managed. nvc is used here because source code is C code, there is nvc++ for compiling C++ code.
The compiler can also tell how the parallel regions are generalized if you pass in a -Minfo option like
$ nvc -acc -gpu=managed -Minfo demo.c
main:
79, Generating implicit copyin(A[:256][:256]) [if not already present]
Generating implicit copy(_error) [if not already present]
Generating implicit copyout(Anew[1:254][1:254]) [if not already present]
83, Loop is parallelizable
85, Loop is parallelizable
Accelerator kernel generated
Generating Tesla code
83, #pragma acc loop gang, vector(4) /* blockIdx.y threadIdx.y */
Generating implicit reduction(max:_error)
85, #pragma acc loop gang, vector(32) /* blockIdx.x threadIdx.x */
91, Generating implicit copyout(A[1:254][1:254]) [if not already present]
Generating implicit copyin(Anew[1:254][1:254]) [if not already present]
95, Loop is parallelizable
97, Loop is parallelizable
Accelerator kernel generated
Generating Tesla code
95, #pragma acc loop gang, vector(4) /* blockIdx.y threadIdx.y */
97, #pragma acc loop gang, vector(32) /* blockIdx.x threadIdx.x */This tells which loops are parallelized with line numbers for reference.
For Windows users that would like to try this SDK, WSL2 is one option. WSL2 does not fully support this SDK at this moment, due to the fact that most virtualization technologies cannot let virtualized systems use the graphic card directly. Nvidia had released a preview driver[2] that allows the Linux subsystem to recognize graphic cards installed on the machine, it allows WSL2 users to compile programs with CUDA toolkits but not with the HPC SDK yet.
Nvidia CUDA WSL2
We are not going to go over how to deal with CUDA on WSL2. We included the installation guide for using CUDA on WSL2 here for anyone's interest [3]. Note that you need to have registered in the Windows Insider Program to get one of the preview Win10 versions.
GCC[4]
GCC has added support to OpenACC since GCC 5. The latest GCC version, GCC 10 has support to OpenACC 2.6.
To compile OpenACC code with GCC, you need to run
gcc -fopenacc demo.cHowever, this does not enable any GPU offloading capability. In order to enable GCC with GPU offloading, we need to build some accelerators by ourselves.
For example, to enable GPU offloading on Nvidia GPUs, you need to rebuild GCC with Nvidia PTX, then use the option -foffload=<target> to offload generated instructions to accelerator devices.
The instruction of building GCC is over complicated therefore will not be shared here.
OpenMP vs OpenACC
We are comparing with OpenMP for two reasons. First, OpenMP is also based on directives to parallelize code; second, OpenMP started support of offloading to accelerators starting OpenMP 4.0 using target constructs. OpenACC uses directives to tell the compiler where to parallelize loops, and how to manage data between host and accelerator memories. OpenMP takes a more generic approach, it allows programmers to explicitly spread the execution of loops, code regions and tasks across teams of threads.
OpenMP's directives tell the compiler to generate parallel code in that specific way, leaving little room to the discretion of the compiler and the optimizer. The compiler must do as instructed. It is up to the programmer to guarantee that generated code is correct, parallelization and scheduling are also responsibility of the programmer, not the compiler at runtime.
OpenACC's parallel directives tells the compiler that the loop is a parallel loop. It is up to the compiler to decide how to parallelize the loop. For example the compiler can generate code to run the iterations across threads, or run the iterations across SIMD lanes. The compiler gets to decide method of parallelization based on the underlying hardware architecture, or use a mixture of different methods.
So the real difference between the two is how much freedom is given to the compilers.
Equivalent directives
Explicit conversions
OpenACC OpenMP
#pragma acc kernels #pragma omp target
{ {
#pragma acc loop worker #pragma omp parallel for private(tmp)
for(int i = 0; i < N; i++){ for(int i = 0; i < N; i++){
tmp = …; tmp = …;
array[i] = tmp * …; array[i] = tmp * …;
} }
#pragma acc loop vector #pragma omp simd
for(int i = 0; i < N; i++) for(int i = 0; i < N; i++)
array2[i] = …; array2[i] = …;
} }ACC parallel
OpenACC OpenMP
#pragma acc parallel #pragma omp target
{ #pragma omp parallel
#pragma acc loop {
for(int i = 0; i < N; i++){ #pragma omp for private(tmp) nowait
tmp = …; for(int i = 0; i < N; i++){
array[i] = tmp * …; tmp = …;
} array[i] = tmp * …;
#pragma acc loop }
for(int i = 0; i < N; i++) #pragma omp for simd
array2[i] = …; for(int i = 0; i < N; i++)
} array2[i] = …;
}ACC Kernels
OpenACC OpenMP
#pragma acc kernels #pragma omp target
{ #pragma omp parallel
for(int i = 0; i < N; i++){ {
tmp = …; #pragma omp for private(tmp)
array[i] = tmp * …; for(int i = 0; i < N; i++){
} tmp = …;
for(int i = 0; i < N; i++) array[i] = tmp * …;
array2[i] = … }
} #pragma omp for simd
for(int i = 0; i < N; i++)
array2[i] = …
}Copy
OpenACC OpenMP
int x[10],y[10]; int x[10],y[10];
#pragma acc data copy(x) copy(y) #pragma omp target data map(x,y)
{ {
... ...
#pragma acc kernels copy(x) copy(y) #pragma omp target update to(x)
{ #pragma omp target map(y)
// Accelerator Code {
... // Accelerator Code
} ...
... }
} }Performance Comparison
Jacobi Iteration
Jacobi iteration is a common algorithm that iteratively computes the solution based on neighbour values. The following code sample is a serial version of 1D Jacobi iteration.
while ( err > tol && iter < iter_max ) {
err=0.0f;
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}OpenMP CPU Implementation
An OpenMP implementation would look like the following, with shared data and reduction on summation values
while ( err > tol && iter < iter_max ) {
err=0.0f;
#pragma omp parallel
{
#pragma omp for shared(nx, Anew, A) reduction(max:err)
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
#pragma omp for shared(nx, Anew, A)
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}
}OpenACC Basic Implementation
A basic OpenACC implementation looks like this.
while ( err > tol && iter < iter_max ) {
err=0.0f;
#pragma acc parallel loop reduction(max:err)
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
#pragma acc parallel loop
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}Or you can let the compiler handle it by using kernel instead of parallel loop. You will be notified during compilation how the compiler thinks this thing should be parallelized.
while ( err > tol && iter < iter_max ) {
err=0.0f;
#pragma acc kernel
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
#pragma acc kernel
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}OpenACC Proper Implementation
The above implementation is actually slower than the serial version, that is due to the fact that there exists data transfer at the end of each iteration. In order to prevent that from happening, we need to copy the data into the accelerator's memory and copy it out when done.
#pragma acc data copyin(A[0:nx]) copyout(Anew[0:nx])
while ( err > tol && iter < iter_max ) {
err=0.0f;
#pragma acc kernel
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
#pragma acc kernel
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}In the above code, we added a copyin(list) for the original matrix of values, and copyout(list) for the computed matrix of results. There are other related directives such as copy(list) which is the combination of both copyin(list) and copyout(list), create(list) for creating a memory region in the accelerator but not copy any data into it, and present(list) which indicates the list is already in the accelerator, which is often used along with create(list)
OpenMP GPU Basic Implementation
Here's the OpenMP GPU basic implementation. Almost everything is the same, just need to enclose everything into an omp target region
while ( err > tol && iter < iter_max ) {
err=0.0f;
#pragma omp target
#pragma omp parallel
{
#pragma omp for shared(nx, Anew, A) reduction(max:err)
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
#pragma omp for shared(nx, Anew, A)
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}
}OpenMP GPU Proper Implementation
Similar to OpenACC, the basic is slow because of data transfer issues, but to optimize OpenMP, you need to explicitly tell the thread how to team up and how to distribute.
#pragma omp target data map(alloc:Anew) map(A)
while ( err > tol && iter < iter_max ) {
err=0.0f;
#pragma omp target teams distribute parallel for reduction(max:error) collapse(2) schedule(static,1)
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
#pragma omp target teams distribute parallel for collapse(2) schedule(static,1)
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}
Execution time
- OpenMP CPU: 1x
- OpenACC Basic: ~2x (twice as slow)
- OpenACC Proper: ~0.14x (7 times faster)
- OpenMP GPU Basic: ~10x (10 times slower)
- OpenMP GPU Proper: ~0.21x (5 times faster)
Collaboration
OpenACC with OpenMP
OpenMP and OpenACC can be used together. Using the example above, we can easily come up with something like
#pragma acc data copyin(A[0:nx]) copyout(Anew[0:nx])
while ( err > tol && iter < iter_max ) {
err=0.0f;
#pragma omp parallel for shared(nx, Anew, A)
#pragma acc kernel
for(int i = 1; i < nx-1; i++) {
Anew[i] = 0.5f * (A[i+1] + A[i-1]);
err = fmax(err, fabs(Anew[i] - A[i]));
}
#pragma omp parallel for shared(nx, Anew, A)
#pragma acc kernel
for( int i = 1; i < nx-1; i++ ) {
A[i] = Anew[i];
}
iter++;
}this way, for each thread created by OpenMP, the computation will be offloaded to an accelerator, with results joined back together.
Combining OpenACC and OpenMP together may be an overkill for the 1D example, a 2D example may be a better fit.
#pragma acc data copy(A), create(Anew)
while ( error > tol && iter < iter_max )
{
error = 0.f;
#pragma omp parallel for shared(m, n, Anew, A)
#pragma acc kernels loop gang(32), vector(16)
for( int j = 1; j < n-1; j++)
{
#pragma acc loop gang(16), vector(32)
for( int i = 1; i < m-1; i++ )
{
Anew[j][i] = 0.25f * ( A[j][i+1] + A[j][i-1]
+ A[j-1][i] + A[j+1][i]);
error = fmaxf( error, fabsf(Anew[j][i]-A[j][i]));
}
}
#pragma omp parallel for shared(m, n, Anew, A)
#pragma acc kernels loop
for( int j = 1; j < n-1; j++)
{
#pragma acc loop gang(16), vector(32)
for( int i = 1; i < m-1; i++ )
{
A[j][i] = Anew[j][i];
}
}
iter++;
}Here we can insert additional instructions into the inner loop on how many gangs and vectors to use. Gang and vector are OpenACC terminologies. A vector is one thread performing single operation on multiple data (SIMD), a worker computes one vector, and a gang comprises of multiple workers that share resource.
OpenACC with MPI
When OpenMP and OpenACC works together, it is usually one CPU with several accelerators as that is how OpenMP works. When there are multiple CPUs and each have access to multiple accelerators, OpenMP will not be enough, and we can introduce MPI. As we learned that MPI is used to allow communication and data transfer between threads during parallel execution. In the case of multiple accelerators, one of the ways we can use the two together is to use MPI to communicate between different accelerators.
The following is a screenshot taken from Nvidia's Advanced OpenACC lecture, showing how does MPI works with OpenACC.

References
https://developer.nvidia.com/blog/benchmarking-cuda-aware-mpi/
https://developer.nvidia.com/hpc-sdk
https://gcc.gnu.org/wiki/OpenACC
https://on-demand.gputechconf.com/gtc/2015/webinar/openacc-course/advanced-openacc-techniques.pdf
https://on-demand.gputechconf.com/gtc/2016/presentation/s6510-jeff-larkin-targeting-gpus-openmp.pdf