Difference between revisions of "Group 6"
(→The Monte Carlo Simulation (PI Calculation)) |
m (→Assignment 3 - Optimize) |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
# [mailto:xhuang110@myseneca.ca?subject=gpu610 Xiaowei Huang] | # [mailto:xhuang110@myseneca.ca?subject=gpu610 Xiaowei Huang] | ||
# [mailto:yyuan34@myseneca.ca?subject=gpu610 Yihang Yuan] | # [mailto:yyuan34@myseneca.ca?subject=gpu610 Yihang Yuan] | ||
| − | |||
| − | [mailto:xhuang110@myseneca.ca,yyuan34 | + | [mailto:xhuang110@myseneca.ca,yyuan34@myseneca.ca?subject=dps901-gpu610 Email All] |
== Progress == | == Progress == | ||
| Line 130: | Line 129: | ||
==== The Monte Carlo Simulation (PI Calculation) ==== | ==== The Monte Carlo Simulation (PI Calculation) ==== | ||
| − | + | The Monte Carlo Simulation (PI Calculation) | |
Got the code from here: | Got the code from here: | ||
https://rosettacode.org/wiki/Monte_Carlo_methods#C.2B.2B | https://rosettacode.org/wiki/Monte_Carlo_methods#C.2B.2B | ||
| Line 136: | Line 135: | ||
It uses random sampling to define constraints on the value and then makes a sort of "best guess." | It uses random sampling to define constraints on the value and then makes a sort of "best guess." | ||
| − | |||
{| class="wikitable mw-collapsible mw-collapsed" | {| class="wikitable mw-collapsible mw-collapsed" | ||
| Line 199: | Line 197: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
As this algorithm is based on random sampling, so there is only one function that does all the work. | As this algorithm is based on random sampling, so there is only one function that does all the work. | ||
| − | |||
Flat profile: | Flat profile: | ||
<pre> | <pre> | ||
| Line 230: | Line 226: | ||
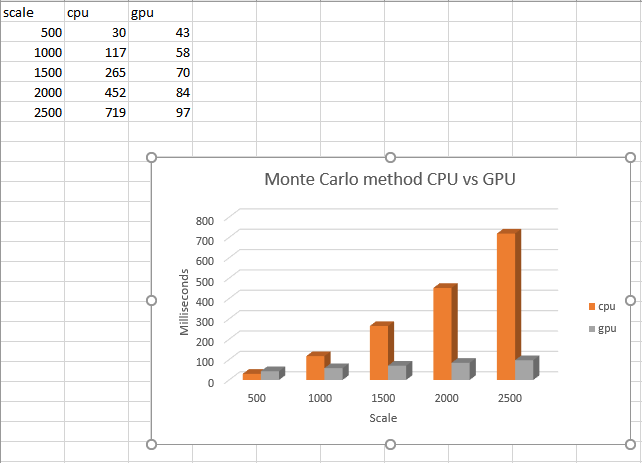
'''Results for different scale of calculation''' | '''Results for different scale of calculation''' | ||
| + | |||
[[File:Yihang.JPG]] | [[File:Yihang.JPG]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Assignment 2 - Parallelize === | === Assignment 2 - Parallelize === | ||
| Line 449: | Line 441: | ||
=== Assignment 3 - Optimize === | === Assignment 3 - Optimize === | ||
| + | The main kernel optimization did on 2 parts | ||
| + | |||
| + | The new '''third kernel''' is to sum up the PI results which generated in each block, by applying serial reduction algorithm which could reduce its Big-O classification is O(log n). Beside, it also sets the limitation to check whether the calculation is out of the range. As it can stop the sum-up to those useless thread value. And the total value of that block is passed to the first element of that block. | ||
| + | <pre> | ||
| + | // kernel 3 | ||
| + | // the third kernel sum the result in each block | ||
| + | __global__ void sumPi(float* d_a, float*d_b, const int n) { | ||
| + | int i = blockIdx.x * blockDim.x + threadIdx.x; | ||
| + | int t = threadIdx.x; | ||
| + | __shared__ float s[ntpb]; | ||
| + | s[t] = d_a[i]; | ||
| + | __syncthreads(); | ||
| + | |||
| + | // sum the data in shared memory | ||
| + | for (int stride = 1; stride < blockDim.x; stride <<= 1) { | ||
| + | if ((t % (2 * stride) == 0) && (i + stride < n)) { | ||
| + | s[t] += s[t + stride]; | ||
| + | } | ||
| + | __syncthreads(); | ||
| + | } | ||
| + | |||
| + | // store the sum in d_b; | ||
| + | if (t == 0) { | ||
| + | d_b[blockIdx.x] = s[0]; | ||
| + | } | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | To reduce the data transfer from device to host, the new '''forth kernel''' is created. It uses to sum up all blocks results from passing back to the host, which also applies the reduction algorithm. | ||
| + | <pre> | ||
| + | // kernel 4 | ||
| + | // the forth kernel sum the result of all blocks | ||
| + | __global__ void accumulate(float* c, const int nblocks) { | ||
| + | // store the elements of c[] in shared memory | ||
| + | int i = blockIdx.x * blockDim.x + threadIdx.x; | ||
| + | int t = threadIdx.x; | ||
| + | __shared__ float s[ntpb]; | ||
| + | s[t] = c[i]; | ||
| + | __syncthreads(); | ||
| + | |||
| + | // sum the data in shared memory | ||
| + | for (int stride = 1; stride < blockDim.x; stride <<= 1) { | ||
| + | if ((t % (2 * stride) == 0) && (i + stride < nblocks)) { | ||
| + | s[t] += s[t + stride]; | ||
| + | } | ||
| + | __syncthreads(); | ||
| + | } | ||
| + | |||
| + | // store the sum in c[0] | ||
| + | if (t == 0) { | ||
| + | c[blockIdx.x] = s[0]; | ||
| + | } | ||
| + | } | ||
| + | </pre> | ||
| + | |||
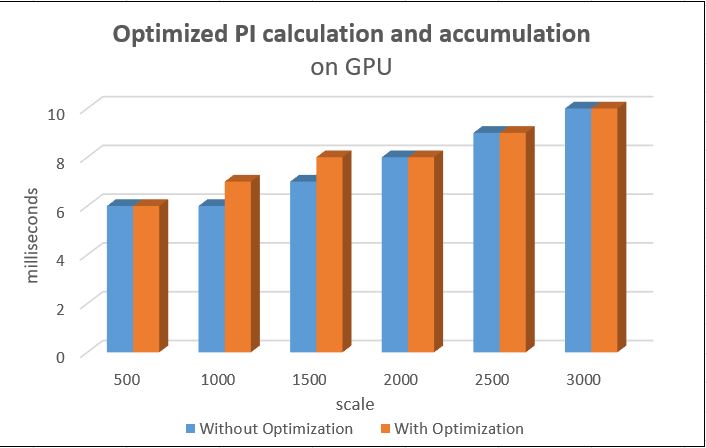
| + | Even though the runtime is closed after implementing the optimization, the kernels has a heavy load than before. It also finishes the accumulation of all randomly generated PI. I consider this optimization performs well. | ||
| + | |||
| + | [[File:Optimized PI calculation and accumulation.jpg]] | ||
Latest revision as of 23:00, 7 April 2019
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
[hide]Group 6
Team Members
Progress
Assignment 1 - Select and Assess
Array Processing
Subject: Array Processing
Blaise Barney introduced Parallel Computing https://computing.llnl.gov/tutorials/parallel_comp/ Array processing could become one of the parallel example, which "demonstrates calculations on 2-dimensional array elements; a function is evaluated on each array element."
Here is my source code
| [Expand] arrayProcessing.cpp |
|---|
Standard random method is used to initialize a 2-dimentional array. The purpose of this program is to perform a 2-dimension array calculation, which is a matrix-matrix multiplication in this example.
In this following profile example, n = 1000
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 100.11 1.48 1.48 multiply(float**, float**, float**, int) 0.68 1.49 0.01 init(float**, int) 0.00 1.49 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z4initPPfi
Call graph
granularity: each sample hit covers 2 byte(s) for 0.67% of 1.49 seconds
index % time self children called name
<spontaneous>
[1] 99.3 1.48 0.00 multiply(float**, float**, float**, int) [1]
-----------------------------------------------
<spontaneous>
[2] 0.7 0.01 0.00 init(float**, int) [2]
-----------------------------------------------
0.00 0.00 1/1 __libc_csu_init [16]
[10] 0.0 0.00 0.00 1 _GLOBAL__sub_I__Z4initPPfi [10]
-----------------------------------------------
�
Index by function name
[10] _GLOBAL__sub_I__Z4initPPfi (arrayProcessing.cpp) [2] init(float**, int) [1] multiply(float**, float**, float**, int)
From the call graph, multiply() took major runtime to more than 99%, as it contains 3 for-loop, which T(n) is O(n^3). Besides, init() also became the second busy one, which has a O(n^2).
As the calculation of elements is independent of one another - leads to an embarrassingly parallel solution. Arrays elements are evenly distributed so that each process owns a portion of the array (subarray). It can be solved in less time with multiple compute resources than with a single compute resource.
The Monte Carlo Simulation (PI Calculation)
The Monte Carlo Simulation (PI Calculation) Got the code from here: https://rosettacode.org/wiki/Monte_Carlo_methods#C.2B.2B A Monte Carlo Simulation is a way of approximating the value of a function where calculating the actual value is difficult or impossible.
It uses random sampling to define constraints on the value and then makes a sort of "best guess."
| [Expand] Source Code |
|---|
As this algorithm is based on random sampling, so there is only one function that does all the work. Flat profile:
Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 101.05 0.02 0.02 calculatePI(int, float*) 0.00 0.02 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z11calculatePIiPf
Call graph
granularity: each sample hit covers 2 byte(s) for 0.47% of 2.11 seconds
index % time self children called name
<spontaneous>
[1] 100.0 2.11 0.00 calculatePI(int, float*) [1]
-----------------------------------------------
0.00 0.00 1/1 __libc_csu_init [17]
[9] 0.0 0.00 0.00 1 _GLOBAL__sub_I__Z11calculatePIiPf [9]
-----------------------------------------------
�
Index by function name
[9] _GLOBAL__sub_I__Z11calculatePIiPf (a1.cpp) [1] calculatePI(int, float*)
Results for different scale of calculation
Assignment 2 - Parallelize
Serial Algorithm:
void calculatePI(int n, float* h_a) {
float x, y;
int hit;
srand(time(NULL));
for (int j = 0; j < n; j++) {
hit = 0;
x = 0;
y = 0;
for (int i = 0; i < n; i++) {
x = float(rand()) / float(RAND_MAX);
y = float(rand()) / float(RAND_MAX);
if (y <= sqrt(1 - (x * x))) {
hit += 1;
}
}
h_a[j] = 4 * float(hit) / float(n);
}
}
Kernels for Parallel Algorithm:
__global__ void setRng(curandState *rng) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
curand_init(123456, idx, 0, &rng[idx]);
}
__global__ void calPI(float* d_a, int n, curandState *rng) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
unsigned int counter = 0;
while (counter < n) {
float x = curand_uniform(&rng[idx]);
float y = curand_uniform(&rng[idx]);
if (y <= sqrt(1 - (x * x))) {
d_a[idx]++;
}
counter++;
}
d_a[idx] = 4.0 * (float(d_a[idx])) / float(n);
}
| [Expand] Full Code |
|---|
Result:
In conclusion, by parallelized the serial version of the algorithm, we see an immediate improvement of performance.
Assignment 3 - Optimize
The main kernel optimization did on 2 parts
The new third kernel is to sum up the PI results which generated in each block, by applying serial reduction algorithm which could reduce its Big-O classification is O(log n). Beside, it also sets the limitation to check whether the calculation is out of the range. As it can stop the sum-up to those useless thread value. And the total value of that block is passed to the first element of that block.
// kernel 3
// the third kernel sum the result in each block
__global__ void sumPi(float* d_a, float*d_b, const int n) {
int i = blockIdx.x * blockDim.x + threadIdx.x;
int t = threadIdx.x;
__shared__ float s[ntpb];
s[t] = d_a[i];
__syncthreads();
// sum the data in shared memory
for (int stride = 1; stride < blockDim.x; stride <<= 1) {
if ((t % (2 * stride) == 0) && (i + stride < n)) {
s[t] += s[t + stride];
}
__syncthreads();
}
// store the sum in d_b;
if (t == 0) {
d_b[blockIdx.x] = s[0];
}
}
To reduce the data transfer from device to host, the new forth kernel is created. It uses to sum up all blocks results from passing back to the host, which also applies the reduction algorithm.
// kernel 4
// the forth kernel sum the result of all blocks
__global__ void accumulate(float* c, const int nblocks) {
// store the elements of c[] in shared memory
int i = blockIdx.x * blockDim.x + threadIdx.x;
int t = threadIdx.x;
__shared__ float s[ntpb];
s[t] = c[i];
__syncthreads();
// sum the data in shared memory
for (int stride = 1; stride < blockDim.x; stride <<= 1) {
if ((t % (2 * stride) == 0) && (i + stride < nblocks)) {
s[t] += s[t + stride];
}
__syncthreads();
}
// store the sum in c[0]
if (t == 0) {
c[blockIdx.x] = s[0];
}
}
Even though the runtime is closed after implementing the optimization, the kernels has a heavy load than before. It also finishes the accumulation of all randomly generated PI. I consider this optimization performs well.
Here is my final source code
| [Expand] p03_reduction.cu |
|---|