Revision as of 21:54, 7 April 2019

GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary

Group 6

Team Members

Progress

Assignment 1 - Select and Assess

Array Processing

Subject: Array Processing

Blaise Barney introduced Parallel Computing https://computing.llnl.gov/tutorials/parallel_comp/ Array processing could become one of the parallel example, which "demonstrates calculations on 2-dimensional array elements; a function is evaluated on each array element."

Here is my source code

arrayProcessing.cpp

 
// arrayProcessing.cpp
// Array processing implement parallel solution 
#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <ctime>

void init(float** randomValue, int n) {
	//std::srand(std::time(nullptr));
    float f = 1.0f / RAND_MAX;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			randomValue[i][j] = std::rand() * f;
}

void multiply(float** a, float** b, float** c, int n) {
    for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++) {
            float sum = 0.0f;
            for (int k = 0; k < n; k++)
				sum += a[i][k] * b[k][j];
            
			c[i][j] = sum;
			if(n <= 10){
				std::cout << "array c[" << i << "," << j << "]: " << c[i][j] << std::endl;
			}
        }
}

int main(int argc, char* argv[]) {
    // interpret command-line argument
    if (argc != 2) {
        std::cerr << argv[0] << ": invalid number of arguments\n"; 
        std::cerr << "Usage: " << argv[0] << "  size_of_matrices\n"; 
		return 1;
    }
    int n  = std::atoi(argv[1]);   // size of matrices

    float** a = new float*[n];
    for (int i = 0; i < n; i++)       
		a[i] = new float[n];
    float** b = new float*[n];
    for (int i = 0; i < n; i++)
        b[i] = new float[n];
    float** c = new float*[n];
    for (int i = 0; i < n; i++)
        c[i] = new float[n];
    
	std::srand(std::time(nullptr));
    init(a, n);
    init(b, n);

    multiply(a, b, c, n);

    for (int i = 0; i < n; i++)
        delete [] a[i];
    delete [] a;
    for (int i = 0; i < n; i++)
        delete [] b[i];
    delete [] b;
    for (int i = 0; i < n; i++)
		delete [] c[i];
    delete [] c;
}

Standard random method is used to initialize a 2-dimentional array. The purpose of this program is to perform a 2-dimension array calculation, which is a matrix-matrix multiplication in this example.

In this following profile example, n = 1000

Flat profile:
Each sample counts as 0.01 seconds.
  %   cumulative   self              self     total           
 time   seconds   seconds    calls  Ts/call  Ts/call  name    
100.11      1.48     1.48                             multiply(float**, float**, float**, int)
  0.68      1.49     0.01                             init(float**, int)
  0.00      1.49     0.00        1     0.00     0.00  _GLOBAL__sub_I__Z4initPPfi

Call graph

granularity: each sample hit covers 2 byte(s) for 0.67% of 1.49 seconds

index % time    self  children    called     name
                                             <spontaneous>
[1]     99.3    1.48    0.00                 multiply(float**, float**, float**, int) [1]
-----------------------------------------------
                                             <spontaneous>
[2]      0.7    0.01    0.00                 init(float**, int) [2]
-----------------------------------------------
                0.00    0.00       1/1       __libc_csu_init [16]
[10]     0.0    0.00    0.00       1         _GLOBAL__sub_I__Z4initPPfi [10]
-----------------------------------------------
�
Index by function name
  [10] _GLOBAL__sub_I__Z4initPPfi (arrayProcessing.cpp) [2] init(float**, int) [1] multiply(float**, float**, float**, int)

From the call graph, multiply() took major runtime to more than 99%, as it contains 3 for-loop, which T(n) is O(n^3). Besides, init() also became the second busy one, which has a O(n^2).

As the calculation of elements is independent of one another - leads to an embarrassingly parallel solution. Arrays elements are evenly distributed so that each process owns a portion of the array (subarray). It can be solved in less time with multiple compute resources than with a single compute resource.

The Monte Carlo Simulation (PI Calculation)

The Monte Carlo Simulation (PI Calculation) Got the code from here: https://rosettacode.org/wiki/Monte_Carlo_methods#C.2B.2B A Monte Carlo Simulation is a way of approximating the value of a function where calculating the actual value is difficult or impossible.

It uses random sampling to define constraints on the value and then makes a sort of "best guess."

Source Code

#include<iostream>
#include<fstream>
#include<math.h>
#include<stdlib.h>
#include<time.h>

using namespace std;

void calculatePI(int n, float* h_a) {
	float x, y;
	int hit;
	srand(time(NULL));
	for (int j = 0; j < n; j++) {
		hit = 0;
		x = 0;
		y = 0;
		for (int i = 0; i < n; i++) {
			x = float(rand()) / float(RAND_MAX);
			y = float(rand()) / float(RAND_MAX);
			if (y <= sqrt(1 - (x * x))) {
				hit += 1;
			}
		}
		h_a[j] = 4 * float(hit) / float(n);
	}
}

int main(int argc, char* argv[]) {

	if (argc != 2) {
		std::cerr << argv[0] << ": invalid number of arguments\n";
		std::cerr << "Usage: " << argv[0] << "  size_of_matrices\n";
		return 1;
	}
	int n = std::atoi(argv[1]); // scale
	float* cpu_a;
	cpu_a = new float[n];


	calculatePI(n, cpu_a);

	ofstream h_file;
	h_file.open("h_result.txt");
	float cpuSum = 0.0f;
	for (int i = 0; i < n; i++) {
		cpuSum += cpu_a[i];
		h_file << "Host: " << cpu_a[i] << endl;
	}
	cpuSum = cpuSum / (float)n;
	cout << "CPU Result: " << cpuSum << endl;
	h_file.close();
}

As this algorithm is based on random sampling, so there is only one function that does all the work. Flat profile:

Each sample counts as 0.01 seconds.
  %   cumulative   self              self     total           
 time   seconds   seconds    calls  Ts/call  Ts/call  name    
101.05      0.02     0.02                             calculatePI(int, float*)
  0.00      0.02     0.00        1     0.00     0.00  _GLOBAL__sub_I__Z11calculatePIiPf

Call graph

granularity: each sample hit covers 2 byte(s) for 0.47% of 2.11 seconds

index % time    self  children    called     name
                                                 <spontaneous>
[1]    100.0    2.11    0.00                 calculatePI(int, float*) [1]
-----------------------------------------------
                0.00    0.00       1/1           __libc_csu_init [17]
[9]      0.0    0.00    0.00       1         _GLOBAL__sub_I__Z11calculatePIiPf [9]
-----------------------------------------------
�
Index by function name

   [9] _GLOBAL__sub_I__Z11calculatePIiPf (a1.cpp) [1] calculatePI(int, float*)

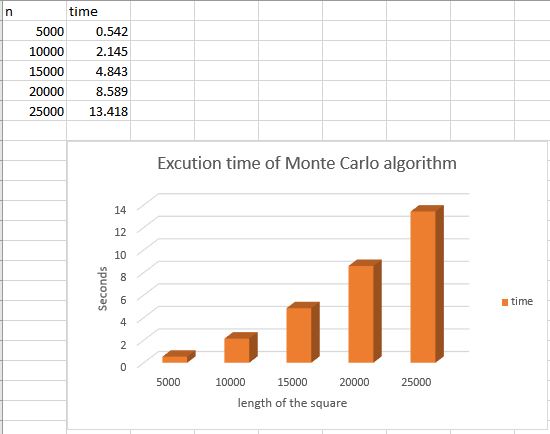
Results for different scale of calculation

Assignment 2 - Parallelize

Serial Algorithm:

void calculatePI(int n, float* h_a) {
	float x, y;
	int hit;
	srand(time(NULL));
	for (int j = 0; j < n; j++) {
		hit = 0;
		x = 0; 
		y = 0;
		for (int i = 0; i < n; i++) {
			x = float(rand()) / float(RAND_MAX);
			y = float(rand()) / float(RAND_MAX);
			if (y <= sqrt(1 - (x * x))) {
				hit += 1;
			}
		}

		h_a[j] = 4 * float(hit) / float(n);

	}
}

Kernels for Parallel Algorithm:

__global__ void setRng(curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	curand_init(123456, idx, 0, &rng[idx]);
}


__global__ void calPI(float* d_a, int n, curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;

	unsigned int counter = 0;
	while (counter < n) {
		float x = curand_uniform(&rng[idx]);
		float y = curand_uniform(&rng[idx]);

		if (y <= sqrt(1 - (x * x))) {
			d_a[idx]++;
		}
		counter++;
	}
	d_a[idx] = 4.0 * (float(d_a[idx])) / float(n);
}

Full Code

#include<iostream>
#include<fstream>
#include<math.h>
#include<stdlib.h>
#include<time.h>
#include <chrono>
#include <cstdlib>
#include <iomanip>

#include <cuda_runtime.h>
#include <curand_kernel.h>
// to remove intellisense highlighting
#include <device_launch_parameters.h>

const int ntpb = 512;
using namespace std;
using namespace std::chrono;

void calculatePI(int n, float* h_a) {
	float x, y;
	int hit;
	srand(time(NULL));
	for (int j = 0; j < n; j++) {
		hit = 0;
		x = 0; 
		y = 0;
		for (int i = 0; i < n; i++) {
			x = float(rand()) / float(RAND_MAX);
			y = float(rand()) / float(RAND_MAX);
			if (y <= sqrt(1 - (x * x))) {
				hit += 1;
			}
		}

		h_a[j] = 4 * float(hit) / float(n);

	}
}

__global__ void setRng(curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	curand_init(123456, idx, 0, &rng[idx]);
}


__global__ void calPI(float* d_a, int n, curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;

	unsigned int counter = 0;
	while (counter < n) {
		float x = curand_uniform(&rng[idx]);
		float y = curand_uniform(&rng[idx]);

		if (y <= sqrt(1 - (x * x))) {
			d_a[idx]++;
		}
		counter++;
	}
	d_a[idx] = 4.0 * (float(d_a[idx])) / float(n);
}



void reportTime(const char* msg, steady_clock::duration span) {
	auto ms = duration_cast<milliseconds>(span);
	std::cout << msg << " took - " <<
		ms.count() << " millisecs" << std::endl;
}
int main(int argc, char* argv[]) {

	if (argc != 2) {
		std::cerr << argv[0] << ": invalid number of arguments\n";
		std::cerr << "Usage: " << argv[0] << "  size_of_matrices\n";
		return 1;
	}
	int n = std::atoi(argv[1]); // scale
	int nblks = (n + ntpb - 1) / ntpb;
	cout << "scale: " << n << endl << endl;
	steady_clock::time_point ts, te;

	float* cpu_a;
	cpu_a = new float[n];

	ts = steady_clock::now();
	calculatePI(n, cpu_a);
	te = steady_clock::now();
	reportTime("CPU", te - ts);




	ofstream h_file;
	h_file.open("h_result.txt");
	float cpuSum = 0.0f;
	for (int i = 0; i < n; i++) {
		cpuSum += cpu_a[i];
		h_file << "Host: " << cpu_a[i] << endl;
	}
	cpuSum = cpuSum / (float)n;
	cout << "CPU Result: " << cpuSum << endl;
	h_file.close();

	cout << endl;
	////////////////////////////////////////

	curandState *d_rng;
	float* d_a;
	float* h_a;
	h_a = new float[n];

	cudaMalloc((void**)&d_a, n * sizeof(float));
	cudaMalloc((void**)&d_rng, n * sizeof(curandState));

	ts = steady_clock::now();

	setRng << < nblks, ntpb >> > (d_rng);
	cudaDeviceSynchronize();	// synchronize [new added]
	calPI << <nblks, ntpb >> > (d_a, n, d_rng);
	cudaDeviceSynchronize();

	te = steady_clock::now();
	reportTime("GPU", te - ts);

	cudaMemcpy(h_a, d_a, n * sizeof(float), cudaMemcpyDeviceToHost);


	ofstream d_file;
	d_file.open("d_result.txt");
	float gpuSum = 0.0f;
	for (int i = 0; i < n; i++) {
		gpuSum += h_a[i];
		d_file << "Device: " << h_a[i] << endl;
	}
	gpuSum = gpuSum / (float)n;
	cout << "GPU Result: " << gpuSum << endl;
	d_file.close();


	delete[] cpu_a;
	delete[] h_a;
	cudaFree(d_a);
	cudaFree(d_rng);

}

Result:

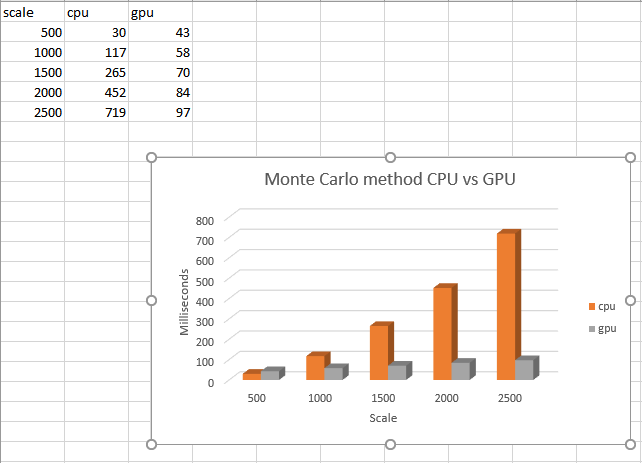
In conclusion, by parallelized the serial version of the algorithm, we see an immediate improvement of performance.

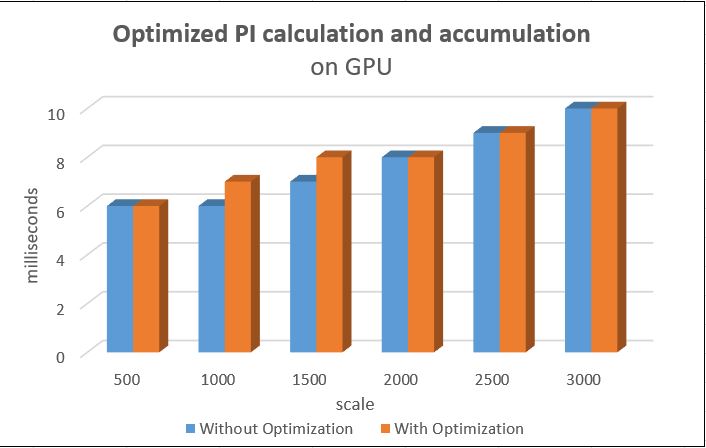
Assignment 3 - Optimize

The main kernel optimization did on 2 parts

The new third kernel is to sum up the PI results which generated in each block, by applying serial reduction algorithm which could reduce its Big-O classification is O(log n). Beside, it also sets the limitation to check whether the calculation is out of the range. As it can stop the sum-up to those useless thread value. And the total value of that block is passed to the first element of that block.

 
// kernel 3 
// the third kernel sum the result in each block 
__global__ void sumPi(float* d_a, float*d_b, const int n) {		 
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	int t = threadIdx.x;
	__shared__ float s[ntpb];
	s[t] = d_a[i];
	__syncthreads();

	// sum the data in shared memory 
	for (int stride = 1; stride < blockDim.x; stride <<= 1) {
		if ((t % (2 * stride) == 0) && (i + stride <  n)) {
			s[t] += s[t + stride];
		}
		__syncthreads();
	}

	// store the sum in d_b; 
	if (t == 0) {
		d_b[blockIdx.x] = s[0];
	}
}

To reduce the data transfer from device to host, the new forth kernel is created. It uses to sum up all blocks results from passing back to the host, which also applies the reduction algorithm.

// kernel 4
// the forth kernel sum the result of all blocks
__global__ void accumulate(float* c, const int nblocks) {
	// store the elements of c[] in shared memory
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	int t = threadIdx.x;
	__shared__ float s[ntpb];
	s[t] = c[i];
	__syncthreads();

	// sum the data in shared memory
	for (int stride = 1; stride < blockDim.x; stride <<= 1) {
		if ((t % (2 * stride) == 0) && (i + stride <  nblocks)) {
			s[t] += s[t + stride];
		}
		__syncthreads();
	}

	// store the sum in c[0]
	if (t == 0) {
		c[blockIdx.x] = s[0];
	}
}

Even though the runtime is closed after implementing the optimization, the kernels has a heavy load than before. It also finishes the accumulation of all randomly generated PI. I consider this optimization performs well.

Here is my final source code

p03_reduction.cu

 
// part 3.1 : reduction
// update 2: 
// add comments to all kernels
// mdf kernel 2 only returns the numbers of dot inside the quadrant, and this number passes to next blocks
// new kernel 3 sums the elements of d_a as generated by the kernel 2, and accumulate the block sums
// new kernel 4 sums all block PI value before passing back to host

#include<iostream>
#include<fstream>
#include<math.h>
#include<stdlib.h>
#include<time.h>
#include <chrono>
#include <cstdlib>
#include <iomanip>

#include <cuda_runtime.h>
#include <curand_kernel.h>
// to remove intellisense highlighting
#include <device_launch_parameters.h>
#ifndef __CUDACC__
#define __CUDACC__
#endif
#include <device_functions.h>

using namespace std;
using namespace std::chrono;
const int ntpb = 512;

// this function uses to calculate PI on CPU 
void calculatePI(int n, float* h_a) {
	float x, y;
	int hit;
	srand(time(NULL));
	for (int j = 0; j < n; j++) {
		hit = 0;
		x = 0;
		y = 0;
		for (int i = 0; i < n; i++) {
			x = float(rand()) / float(RAND_MAX);
			y = float(rand()) / float(RAND_MAX);
			if (y <= sqrt(1 - (x * x))) {
				hit += 1;
			}
		}

		h_a[j] = 4 * float(hit) / float(n);

	}
}


// kernel 1
// The first kernel uses to generate random numbers 
__global__ void setRng(curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	curand_init(123456, idx, 0, &rng[idx]);
}

// kernel 2
// The second kernel identifis the dot location (use the kernel 1 passed random number to create) 
// whether it is been in the quadrant or not 
__global__ void calPI(float* d_a, int n, curandState *rng) {
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	unsigned int counter = 0;		// this variable counts the total number of dot be placed
	unsigned int hit = 0;			// this variable counts the number of dot inside the cirle
	
	// in one Threat, it generates n dots
	while (counter < n) {
		float x = curand_uniform(&rng[idx]);
		float y = curand_uniform(&rng[idx]);

		if (y*y <= (1 - (x * x))) {
			hit++;
		}
		counter++;
	}

	d_a[idx] = 4.0 * (float(hit)) / float(n);
}

// kernel 3 
// the third kernel sum the result in each block 
__global__ void sumPi(float* d_a, float*d_b, const int n) {		 
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	int t = threadIdx.x;
	__shared__ float s[ntpb];
	s[t] = d_a[i];
	__syncthreads();

	// sum the data in shared memory 
	for (int stride = 1; stride < blockDim.x; stride <<= 1) {
		if ((t % (2 * stride) == 0) && (i + stride <  n)) {
			s[t] += s[t + stride];
		}
		__syncthreads();
	}

	// store the sum in d_b; 
	if (t == 0) {
		d_b[blockIdx.x] = s[0];
	}
}

// kernel 4
// the forth kernel sum the result of all blocks
__global__ void accumulate(float* c, const int nblocks) {
	// store the elements of c[] in shared memory
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	int t = threadIdx.x;
	__shared__ float s[ntpb];
	s[t] = c[i];
	__syncthreads();

	// sum the data in shared memory
	for (int stride = 1; stride < blockDim.x; stride <<= 1) {
		if ((t % (2 * stride) == 0) && (i + stride <  nblocks)) {
			s[t] += s[t + stride];
		}
		__syncthreads();
	}

	// store the sum in c[0]
	if (t == 0) {
		c[blockIdx.x] = s[0];
	}
}

void reportTime(const char* msg, steady_clock::duration span) {
	auto ms = duration_cast<milliseconds>(span);
	std::cout << msg << " took - " <<
		ms.count() << " millisecs" << std::endl;
}

int main(int argc, char* argv[]) {

	if (argc != 2) {
		std::cerr << argv[0] << ": invalid number of arguments\n";
		std::cerr << "Usage: " << argv[0] << "  size_of_matrices\n";
		return 1;
	}
	int n = std::atoi(argv[1]); // scale
	int nblks = (n + ntpb - 1) / ntpb;

	cout << "scale: " << n << endl << endl;
	steady_clock::time_point ts, te;

	float* cpu_a;
	cpu_a = new float[n];

	ts = steady_clock::now();
	calculatePI(n, cpu_a);
	te = steady_clock::now();
	reportTime("CPU", te - ts);


	ofstream h_file;
	h_file.open("h_result.txt");
	float cpuSum = 0.0f;
	for (int i = 0; i < n; i++) {
		cpuSum += cpu_a[i];
		h_file << "Host: " << cpu_a[i] << endl;
	}
	cpuSum = cpuSum / (float)n;
	cout << "CPU Result: " << cpuSum << endl;
	h_file.close();

	cout << endl;
	////////////////////////////////////////

	curandState *d_rng;
	float* d_a;
	float* d_b;
	float* h_a;
	h_a = new float[n];

	cudaMalloc((void**)&d_a, n * sizeof(float));
	cudaMalloc((void**)&d_b, n * sizeof(float));
	cudaMalloc((void**)&d_rng, n * sizeof(curandState));

	ts = steady_clock::now();

	setRng << < nblks, ntpb >> > (d_rng);
	cudaDeviceSynchronize();

	// calculate PI in each thread and pass its value
	calPI << <nblks, ntpb >> > (d_a, n, d_rng);
	cudaDeviceSynchronize();

	// sum PI in total and pass back on the device
	sumPi << <nblks, ntpb >> > (d_a, d_b, n);	
	cudaDeviceSynchronize();

	// accumulate the block sums 
	accumulate << <1, nblks >> >(d_b, nblks);
	cudaDeviceSynchronize();

	te = steady_clock::now();
	reportTime("GPU", te - ts);

	// host h_a only receives one element from device d_b
	cudaMemcpy(h_a, d_b, n * sizeof(float), cudaMemcpyDeviceToHost);


	ofstream d_file;
	d_file.open("d_result.txt");
	float gpuSum = 0.0f;
	gpuSum = h_a[0] / (float)n;
	cout << "GPU Result: " << gpuSum << "\n \n"<< endl;
	d_file.close();

	cudaFree(d_a);
	cudaFree(d_rng);
	delete[] cpu_a;
	delete[] h_a;

	// reset the device
	cudaDeviceReset();
}

Revision as of 21:50, 7 April 2019 (view source) Xhuang110 (talk \| contribs) m (→‎Assignment 3 - Optimize) ← Older edit		Revision as of 21:54, 7 April 2019 (view source) Xhuang110 (talk \| contribs) (→‎Assignment 3 - Optimize) Newer edit →
Line 729:		Line 729:

	\|}		\|}
		+
		+	[[File:Optimized PI calculation and accumulation.jpg]]

Difference between revisions of "Group 6"

Revision as of 21:54, 7 April 2019

Contents

Group 6

Team Members

Progress

Assignment 1 - Select and Assess

Array Processing

The Monte Carlo Simulation (PI Calculation)

Assignment 2 - Parallelize

Serial Algorithm:

Assignment 3 - Optimize

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

get involved with CDOT

courses

course projects

links

Tools