Difference between revisions of "Pixels"
(→Part 2) |
(→Cholesky) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 34: | Line 34: | ||
With Mr Szalwinski's advice we've starting looking into how to invert a matrix and use NVidia's cuSOLVER library. Our research has shown that by inverting a Matrix we are solving linear system of equations. And if the goal is to solve equations there are better ways of doing so. <br/><br/> | With Mr Szalwinski's advice we've starting looking into how to invert a matrix and use NVidia's cuSOLVER library. Our research has shown that by inverting a Matrix we are solving linear system of equations. And if the goal is to solve equations there are better ways of doing so. <br/><br/> | ||
| − | NVidia cuSOLVER library provides hight-level API functions for common matrix factorization and triangular solve routines for dense matrices. While it also provides routines for sparse matrix factorization it lies beyond the scope of this | + | NVidia cuSOLVER library provides hight-level API functions for common matrix factorization and triangular solve routines for dense matrices. While it also provides routines for sparse matrix factorization it lies beyond the scope of this assi |
| + | ---- | ||
| + | gnment. Our code includes 3 factorization methods on the GPU: LU, QR and Cholesky decomposition as well as LU decomposition on CPU to benchmark the runtimes. <br/><br/> | ||
| − | [[File:file9.png|500px]] | + | [[File:file9.png|500px]] <br/> |
| − | + | <b>This methods involves</b> <br/> | |
| + | 1. Transformation of the original matrix into two parts - lower and upper, such that if we multiply them together we get the original matrix. Since the lower matrix has 1's in its diagonal we only need to store everything below that. This effectively means that both upper and lower matrices could be stored in the original matrix's size. However extra space is needed for the calculations.<br/> | ||
| + | 2. Having two triangular matrices we are able to solve the equation by either forward-backword substitution or Gaussian elimination.<br/><br/> | ||
| + | |||
| + | [[File:file10.png|800px]] <br/><br/> | ||
| + | The code above (PART 1) creates a matrix of NxN size and two vectors of N size. To solve for b1 in A*b1=b. It then uses cblas level 2 function for Matrix * Vector multiplication to get a result.<br/><br/> | ||
| + | [[File:file11.png|750px]] <br/><br/> | ||
| + | The code above (PART 2) creates and allocates memory on the device and on line 54 calculates the size required for factorization even though the end result will be stored in the original matrix. On line 61 the function <code>cusolverDnDget | ||
| + | ---- | ||
| + | rf()</code> uses d_A matrix and decomposes it into two triangular matrices with partial pivoting (only rows exchanged). On line 62 <code>cusolverDnDgetrs()</code> solves triangular system by USING two triangular matrices stored in d_A AND a result we calculated earlier in d_B. The output of this function is a vector which is placed in d_B. At this point the resulting vector d_B should match the initialized B1 vector on line 29. This is how we know we have solved. <br/><br/> | ||
| + | |||
| + | Similar decomposition can be found in QR and Cholesky | ||
| + | |||
| + | ---- | ||
| + | |||
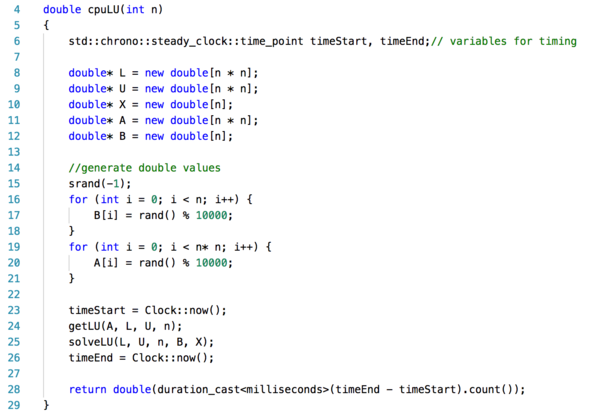
| + | === LU decomposition on the CPU is presented below with Big O(n^3) runtime === | ||
| + | ===== Runner ===== | ||
| + | [[File:file12.png|600px]] <br/><br/> | ||
| + | ===== Solvers ===== | ||
| + | [[File:file13.png|700px]] <br/><br/> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | === Run Times === | ||
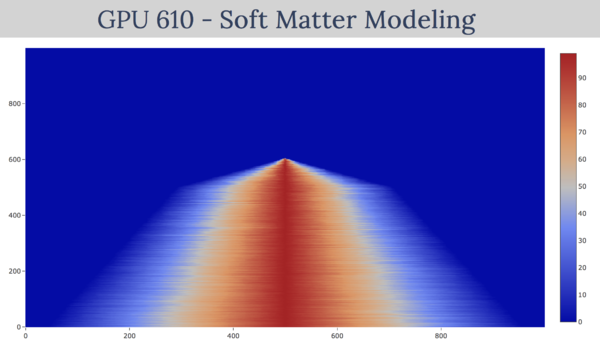
| + | We have decided to include the information about GPU in our final output as we were testing it on different graphics cards.<br/> | ||
| + | [[File:file14.png|700px]][[File:resultPixels.png|700px]] <br/><br/> | ||
| + | Looking at the Matrix size of 10,000 x 10,000 the LU decomposition on GPU runs about <b>39 times</b> faster then CPU, which is substantial improvements in the runtimes. <br/><br/> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | It is also interesting to note the difference in runtime between LU, QR and Cholesky methods. <br/> | ||
| + | [[File:resultPixels2.png|500px]] | ||
| + | ===== QR ===== | ||
| + | QR is ideal if the matrix you are using needs to be transformed into an orthogonal matrix at some point. This method would be combining two tasks into one. | ||
| + | |||
| + | =====Cholesky ===== | ||
| + | Ideal if the matrix you are working with is already symmetrical. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | <br/><br/> The complete code can be found at Github repo [https://github.com/YuriyKartuzov/cuSOLVER HERE] | ||
Latest revision as of 22:04, 16 April 2018
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
Pixels
Team Members
Progress
Part 1
In part one we were looking at using CImg c++ library to optize the code.
(Yuriy Kartuzov)One idea was to use ASCII art, by taking a grayscale image and turning it into a text file. Each individual character would represent a portion of an image. It was important to keep the ratio or x, y pixels fixed and equal to that of monospace font. We estimated that to be about 8x:5y. Below is a sample of original and ascii art image.


Scaling of characters is problematic when fonts size gets smaller then 4-5 pixels, so image above is of lower quality then otherwise possible. If we zoom in then individual characters become visible


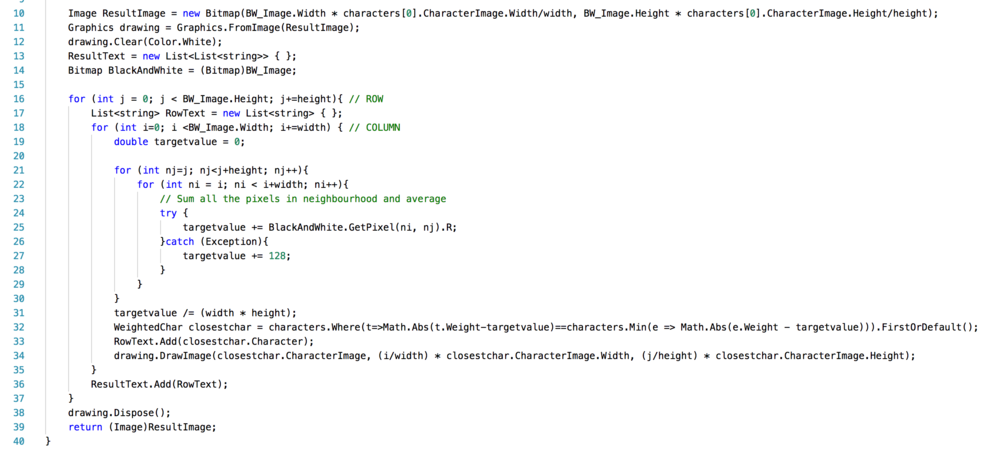
The idea was to take a handful of pixels and average it to a single grayscale value. It is possible because each pixel's luminosity is expressed as a single value from 0 - 255. Then we would create a look up table of how each character is mapped to the same grayscale value. During our research we found that there is an unofficial standard 70 characters.

The following code is a snippet that does most of the work described. It has 4 nested for-loops - a prime candidate for parallelization.
I was going to use CImg library to import and image and get at it's pixel data. However on a MAC there was an issue, it complained about X11 library not being found (Mac dropped support for X11). There is open-source project that can be installed on the Mac www.xquartz.org, however that did not help. I tried setting different flags in CImg header file without success.
I moved on to trying to code my own BMP decoder by reading specification for this file format found here. This proved to be harder that I thought since each BMP file is split into 4 parts: File header, Info header, RGB array and colour-index (actual data). And parsing would depend on different flags in those headers, which was way more work then I was willing to take on. This also was pretty far from course curriculum of putting the code on GPU.
(Adam Kolodko) was looking into taking a function from CImg library that is used to resize the image.

However this function uses different approaches to do that depending on the size of the image and other properties, which meant that optimized code would only run in certain cases. And also it already has multithreading implemented for some of it's computationally intensive tasks.
We also played with the idea of modelling/plotting large data interactively in the browser by using Plotly.JS, the website could be found here
Part 2
With Mr Szalwinski's advice we've starting looking into how to invert a matrix and use NVidia's cuSOLVER library. Our research has shown that by inverting a Matrix we are solving linear system of equations. And if the goal is to solve equations there are better ways of doing so.
NVidia cuSOLVER library provides hight-level API functions for common matrix factorization and triangular solve routines for dense matrices. While it also provides routines for sparse matrix factorization it lies beyond the scope of this assi
gnment. Our code includes 3 factorization methods on the GPU: LU, QR and Cholesky decomposition as well as LU decomposition on CPU to benchmark the runtimes.
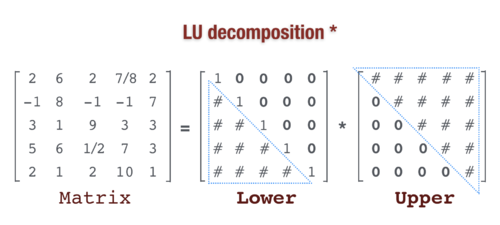
This methods involves
1. Transformation of the original matrix into two parts - lower and upper, such that if we multiply them together we get the original matrix. Since the lower matrix has 1's in its diagonal we only need to store everything below that. This effectively means that both upper and lower matrices could be stored in the original matrix's size. However extra space is needed for the calculations.
2. Having two triangular matrices we are able to solve the equation by either forward-backword substitution or Gaussian elimination.
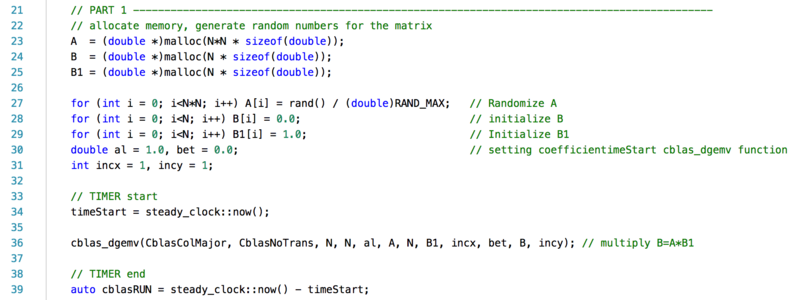
The code above (PART 1) creates a matrix of NxN size and two vectors of N size. To solve for b1 in A*b1=b. It then uses cblas level 2 function for Matrix * Vector multiplication to get a result.

The code above (PART 2) creates and allocates memory on the device and on line 54 calculates the size required for factorization even though the end result will be stored in the original matrix. On line 61 the function cusolverDnDget
rf() uses d_A matrix and decomposes it into two triangular matrices with partial pivoting (only rows exchanged). On line 62 cusolverDnDgetrs() solves triangular system by USING two triangular matrices stored in d_A AND a result we calculated earlier in d_B. The output of this function is a vector which is placed in d_B. At this point the resulting vector d_B should match the initialized B1 vector on line 29. This is how we know we have solved.
Similar decomposition can be found in QR and Cholesky
LU decomposition on the CPU is presented below with Big O(n^3) runtime
Runner
Solvers
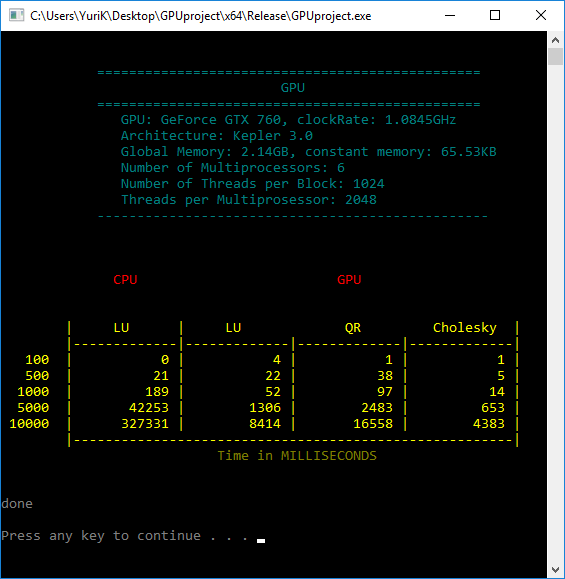
Run Times
We have decided to include the information about GPU in our final output as we were testing it on different graphics cards.
![]()
Looking at the Matrix size of 10,000 x 10,000 the LU decomposition on GPU runs about 39 times faster then CPU, which is substantial improvements in the runtimes.
It is also interesting to note the difference in runtime between LU, QR and Cholesky methods.
![]()
QR
QR is ideal if the matrix you are using needs to be transformed into an orthogonal matrix at some point. This method would be combining two tasks into one.
Cholesky
Ideal if the matrix you are working with is already symmetrical.
The complete code can be found at Github repo HERE