Difference between revisions of "Team NP Complete"
Jali-clarke (talk | contribs) (→Initial Performance) |
(→OpenMP) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 23: | Line 23: | ||
OpenMP is a parallel programming API provided by Intel for C, C++, and Fortran. It enables flexible implementation of parallel algorithms, allowing computers of all builds to utilize all cores it has access to. | OpenMP is a parallel programming API provided by Intel for C, C++, and Fortran. It enables flexible implementation of parallel algorithms, allowing computers of all builds to utilize all cores it has access to. | ||
| − | In this project, the <nowiki>#pragma omp parallel for</nowiki> statement was used in several locations in the program where for loops had no | + | In this project, the <nowiki>#pragma omp parallel for</nowiki> statement was used in several locations in the program where for loops had no dependencies. Where there were dependencies, math was used in such a way that the for loops no longer had the dependencies. Their usage will be discussed further down. |
=Program= | =Program= | ||
| − | ==Without | + | ==Without OpenMP== |
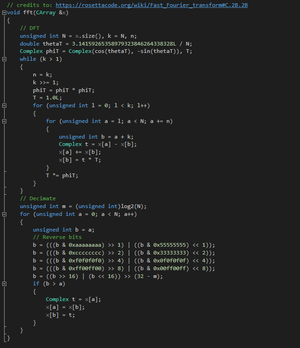
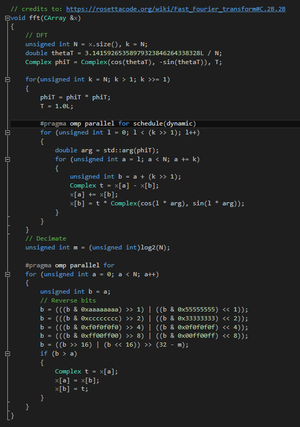
[[File:FFT.png|thumb|fig 3.1 Fourier transformation code block.]] | [[File:FFT.png|thumb|fig 3.1 Fourier transformation code block.]] | ||
| Line 38: | Line 38: | ||
[[File:NonParallel.png|1000px|center|Non-Parallel Process]] | [[File:NonParallel.png|1000px|center|Non-Parallel Process]] | ||
| − | + | ==With OpenMP and Optimization== | |
| − | ==With | ||
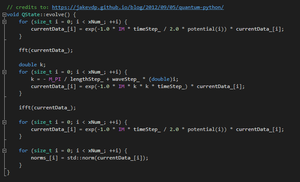
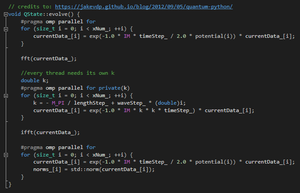
[[File:PFFT.png|thumb|fig 4.1 Fourier transformation code block, with OpenMP parallelization.]] | [[File:PFFT.png|thumb|fig 4.1 Fourier transformation code block, with OpenMP parallelization.]] | ||
[[File:PFT.png|thumb|fig 4.2 Fourier transformations called in OpenMP.]] | [[File:PFT.png|thumb|fig 4.2 Fourier transformations called in OpenMP.]] | ||
| Line 48: | Line 47: | ||
[[File:Parallel.png|1000px|center|Non-Parallel Process]] | [[File:Parallel.png|1000px|center|Non-Parallel Process]] | ||
| − | |||
=Comparison and Analysis= | =Comparison and Analysis= | ||
| Line 67: | Line 65: | ||
We parallelized the code for rendering and state evolution above. We did not, however, yet parallelize the FFT code. The reason for this is that we initially thought that there was a loop-carried dependency that could not be resolved: | We parallelized the code for rendering and state evolution above. We did not, however, yet parallelize the FFT code. The reason for this is that we initially thought that there was a loop-carried dependency that could not be resolved: | ||
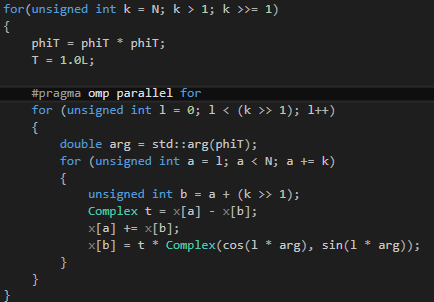
| − | [[File:FFT_crop.png| | + | [[File:FFT_crop.png|500px|none|Hotspot]] |
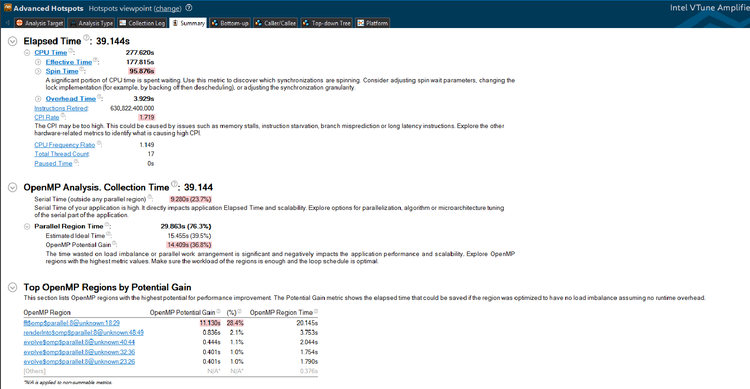
The issue is the <code>T *= phiT;</code> line. This means that every time the loop counter <code>l</code> increases, <code>T</code> gets multiplied by <code>phiT</code>. This statement seems painfully obvious, but it prevents us from parallelizing the code since the iterations can't be done in an arbitrary order. What it does mean, however, is that we can remove that line and replace any usage of <code>T</code> with <code>pow(phiT, l)</code>. We can then parallelize it, since the iterations are now order-invariant. When we do that, the FPS somehow does not change. In fact, if we remove the parallel for construct, the FPS drops to a meager 1 frame per second. This is awful, and likely because the <code>pow()</code> operation is very computationally expensive. Are we stuck? Of course not. We can apply math. There is a property of complex numbers which allows us to turn exponentiation into multiplication. If we write the complex number <code>phiT</code> as <code>phiT = cos(arg) + i * sin(arg)</code>, and we can since it has norm 1, we have <code>phiT ** l = cos(l * arg) + i * sin(l * arg)</code>. This gave a tremendous speedup since the trigonometric functions are apparently less costly than exponentiation. The code and new vTune analyses are below. | The issue is the <code>T *= phiT;</code> line. This means that every time the loop counter <code>l</code> increases, <code>T</code> gets multiplied by <code>phiT</code>. This statement seems painfully obvious, but it prevents us from parallelizing the code since the iterations can't be done in an arbitrary order. What it does mean, however, is that we can remove that line and replace any usage of <code>T</code> with <code>pow(phiT, l)</code>. We can then parallelize it, since the iterations are now order-invariant. When we do that, the FPS somehow does not change. In fact, if we remove the parallel for construct, the FPS drops to a meager 1 frame per second. This is awful, and likely because the <code>pow()</code> operation is very computationally expensive. Are we stuck? Of course not. We can apply math. There is a property of complex numbers which allows us to turn exponentiation into multiplication. If we write the complex number <code>phiT</code> as <code>phiT = cos(arg) + i * sin(arg)</code>, and we can since it has norm 1, we have <code>phiT ** l = cos(l * arg) + i * sin(l * arg)</code>. This gave a tremendous speedup since the trigonometric functions are apparently less costly than exponentiation. The code and new vTune analyses are below. | ||
| − | [[File:PFFT_crop_no_dynamic.png| | + | [[File:PFFT_crop_no_dynamic.png|500px|none|No dynamic]] |
| − | [[File:after_fft_analysis.png| | + | [[File:after_fft_analysis.png|750px|none|After FFT analysis]] |
| − | [[File:after_fft_hist.png| | + | [[File:after_fft_hist.png|750px|none|After FFT analysis]] |
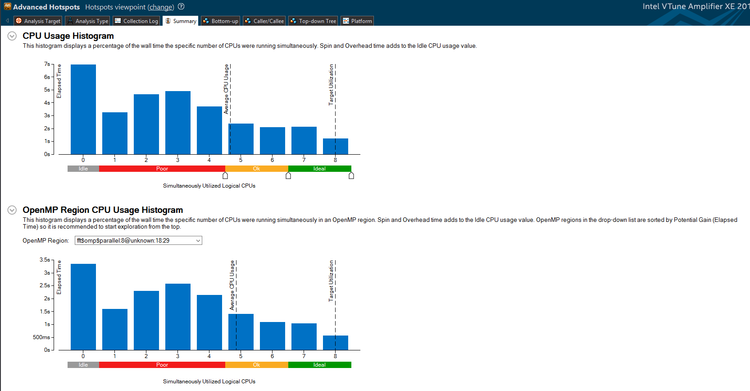
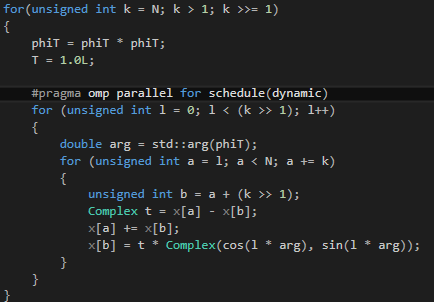
So we've better parallelized the program by attacking a computationally expensive loop which runs many times. We have achieved a massive speedup. That said, it seems that a lot of CPU time is spent idle, especially in the region we have just parallelized. (In addition, the FPS is not very stable). This is because each loop iteration is guaranteed to do a different amount of work. When the loop counter <code>l</code> is small, the inner loop runs many times. When it is large, it does not. This is most easily fixed by adding dynamic scheduling. | So we've better parallelized the program by attacking a computationally expensive loop which runs many times. We have achieved a massive speedup. That said, it seems that a lot of CPU time is spent idle, especially in the region we have just parallelized. (In addition, the FPS is not very stable). This is because each loop iteration is guaranteed to do a different amount of work. When the loop counter <code>l</code> is small, the inner loop runs many times. When it is large, it does not. This is most easily fixed by adding dynamic scheduling. | ||
| − | [[File:PFFT_crop.png| | + | [[File:PFFT_crop.png|500px|none|Dynamic]] |
| − | [[File:after_dynamic_analysis.png| | + | [[File:after_dynamic_analysis.png|750px|none|Dynamic Performance]] |
| − | [[File:after_dynamic_histo.png| | + | [[File:after_dynamic_histo.png|750px|none|Dynamic Histogram]] |
As the analyses show, that loop now shows more efficient CPU usage. It also gave a slightly higher, stabilized FPS. | As the analyses show, that loop now shows more efficient CPU usage. It also gave a slightly higher, stabilized FPS. | ||
Latest revision as of 11:58, 22 December 2017
Contents
Simulating Quantum Tunneling With OpenMP
Members:
Introduction
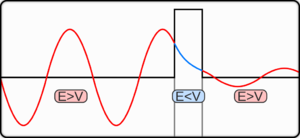
The concept of quantum tunneling is a subset of the Quantum Mechanics branch of theoretical physics. The core concept of Quantum Mechanics is that on a microscopic level, particles behave strangely, often in counter-intuitive ways. Quantum Tunneling refers to the phenomenon in which particles pass through barriers if the particles have enough energy and if the barrier is thin enough. In essence, said particles 'ignore' the barrier, continuing on as if nothing were there at all.
Visualizing
A good way to contrast quantum tunneling with intuition is to consider the following scenario: picture yourself at the bottom of a large hill. You have a tennis ball that you want to roll up the hill far enough that it rolls down the other side. If you don't give it enough energy to reach the top of the hill, the ball will merely roll back to you.
Now replace the tennis ball with an electron. The electron, intuitively, would require a specific amount of energy needed to surpass a barrier, such as a gap of air. However, quantum mechanics and intuition tend not to occupy the same space! The electron, instead, always has a probability of passing through the barrier without ever having come in contact with the barrier in the first place. If this happens, the electron's probability will from there on out be lower than it was prior to tunneling through the barrier.
Keep in mind: this really only happens on the particle level, and not even to all particles. Only particles with low mass and high energy are capable of quantum tunneling, at least consistently.
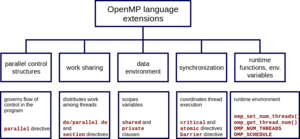
OpenMP
OpenMP is a parallel programming API provided by Intel for C, C++, and Fortran. It enables flexible implementation of parallel algorithms, allowing computers of all builds to utilize all cores it has access to.
In this project, the #pragma omp parallel for statement was used in several locations in the program where for loops had no dependencies. Where there were dependencies, math was used in such a way that the for loops no longer had the dependencies. Their usage will be discussed further down.
Program
Without OpenMP
Originally, this program would calculate the path of a particle using Fourier transformations. These were used in place of the time resource consuming Schrodinger equations because the Schrodinger equations require the simulation to take into account, at each point: the potential energy after a half step, the kinetic energy after a whole step, then finally going back to take the potential energy of the half step. This was even more complicated because, for each particle, every neighboring particle had to be analyzed and accounted for as well. The Fourier transformations converted this into a simple process of multiplication, as shown in the code in figure 1.2:
After the values for all the particles' energies are calculated, they are rendered on the screen. Also rendered on the top left are the frames per second being rendered on the screen.
With OpenMP and Optimization
With the introduction of OpenMP into this project, several processes could be done in parallel. In the evolve() function, whenever a for loop was called, it could be parallelized because none of them had external variable dependencies. That eliminated quite a bit of overhead in the runtime. With the inclusion of OpenMP, the Fourier function, itself, was condensed substantially. This was achieved by introducing the Complex type into the program, so that complex calculations could be done in-line. The dynamic call to #pragma omp parallel also cut out a considerable amount of idle time that the CPU spent waiting to initialized all the threads that the program indicated that it required, rather than created threads on a need basis.
On this screen, the parallelized version of this code is running. Observe that the framerate is considerably better than the non-OpenMP program.
Comparison and Analysis
Initial Performance
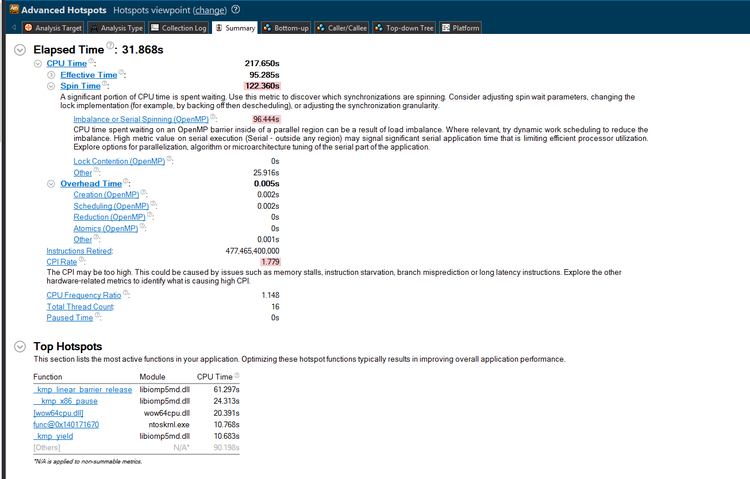
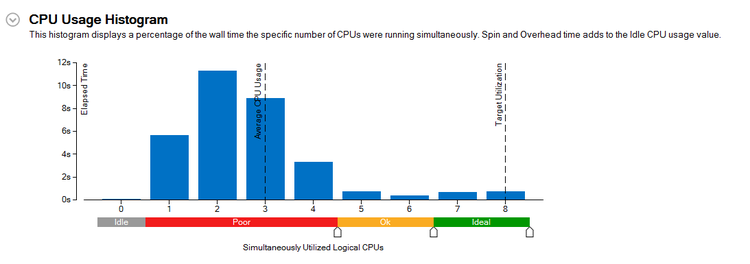
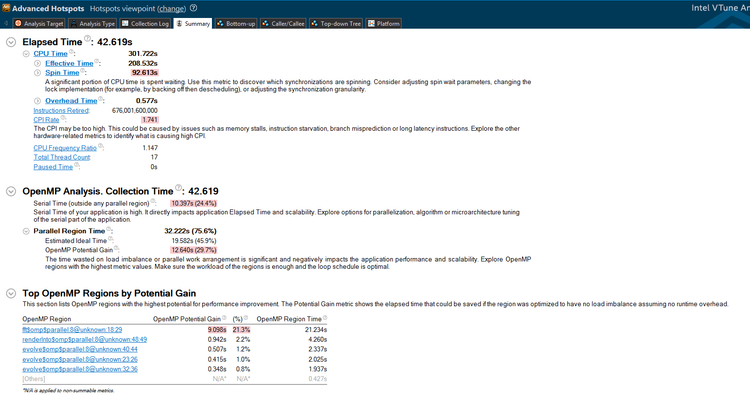
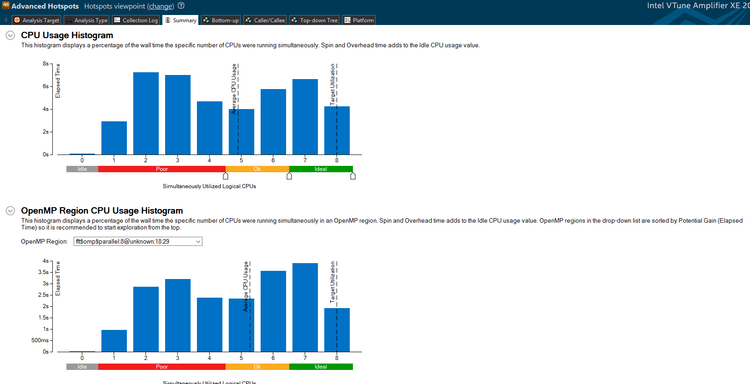
Below, you can see the analysis provided by the VTune Amplifier, through visual studio. Here we can see the total elapsed time as well as the overhead time that the program used:
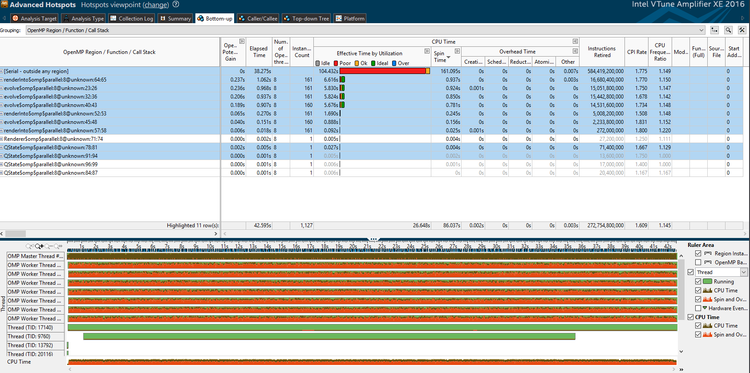
What these graphs and figures are telling us is that we've efficiently parallelized the lowest of the low hanging fruit. The parallel regions themselves are reasonably efficient at what they do, but as it turns out, they contributed very, very little to the computational load in the first place. A lot of CPU time is spent at synchronization barriers, and there is a major hotspot which can still be parallelized.
Parallelized and Dynamic Performance
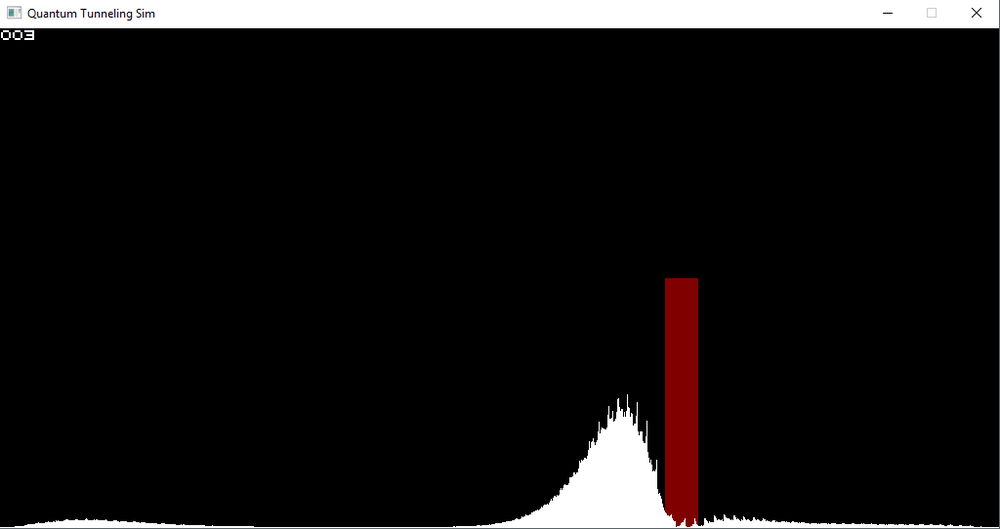
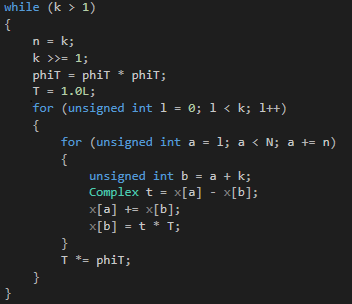
We parallelized the code for rendering and state evolution above. We did not, however, yet parallelize the FFT code. The reason for this is that we initially thought that there was a loop-carried dependency that could not be resolved:
The issue is the T *= phiT; line. This means that every time the loop counter l increases, T gets multiplied by phiT. This statement seems painfully obvious, but it prevents us from parallelizing the code since the iterations can't be done in an arbitrary order. What it does mean, however, is that we can remove that line and replace any usage of T with pow(phiT, l). We can then parallelize it, since the iterations are now order-invariant. When we do that, the FPS somehow does not change. In fact, if we remove the parallel for construct, the FPS drops to a meager 1 frame per second. This is awful, and likely because the pow() operation is very computationally expensive. Are we stuck? Of course not. We can apply math. There is a property of complex numbers which allows us to turn exponentiation into multiplication. If we write the complex number phiT as phiT = cos(arg) + i * sin(arg), and we can since it has norm 1, we have phiT ** l = cos(l * arg) + i * sin(l * arg). This gave a tremendous speedup since the trigonometric functions are apparently less costly than exponentiation. The code and new vTune analyses are below.
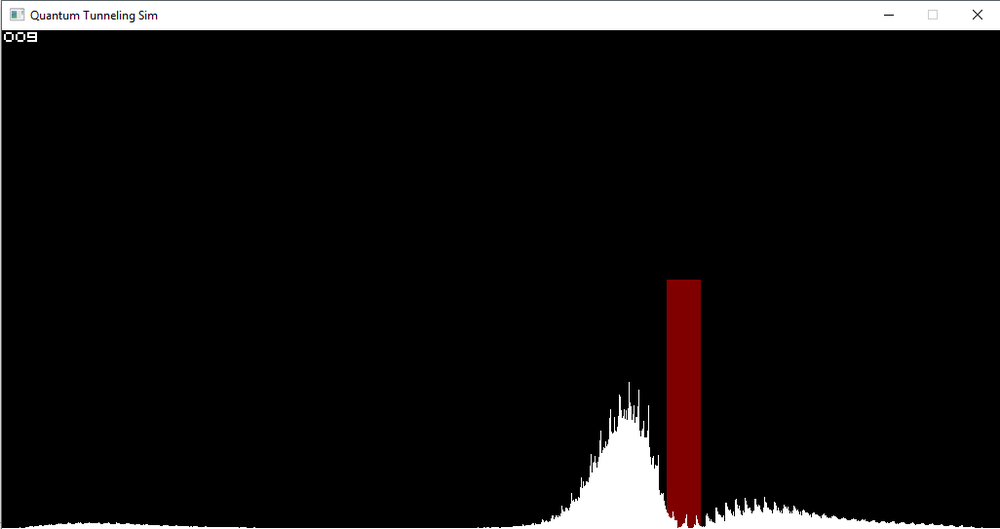
So we've better parallelized the program by attacking a computationally expensive loop which runs many times. We have achieved a massive speedup. That said, it seems that a lot of CPU time is spent idle, especially in the region we have just parallelized. (In addition, the FPS is not very stable). This is because each loop iteration is guaranteed to do a different amount of work. When the loop counter l is small, the inner loop runs many times. When it is large, it does not. This is most easily fixed by adding dynamic scheduling.
As the analyses show, that loop now shows more efficient CPU usage. It also gave a slightly higher, stabilized FPS.
Conclusion
After countless hours programming this simulation, incorporating OpenMP into the finished program did not prove to be very difficult. The most challenging part of including it was identifying the bottleneck for the performance, where CPU idle time was occurring. After the Fourier Transformation Function was identified as the cause of the bottleneck, the loop-carried dependency was factored out and an OpenMP for loop was added. After observing that there was still a considerable amount of CPU idle time, the program was changed to include a dynamic version of the OpenMP for loop, which indicated to the program to dynamically load-balance threads, as opposed to wasting time creating a (statically) set amount of threads that it may not have much to actually compute. After the dynamic scheduling was added, the program jumped to a consistent efficiency and run time.