Difference between revisions of "Team NP Complete"
| Line 1: | Line 1: | ||
| + | = Simulating Quantum Tunneling With OpenMP = | ||
| + | |||
Members: | Members: | ||
# [mailto:jali-clarke@myseneca.ca?subject=DPS921 Jinnah Ali-Clarke] | # [mailto:jali-clarke@myseneca.ca?subject=DPS921 Jinnah Ali-Clarke] | ||
# [mailto:claffan@myseneca.ca?subject=DPS921 Cassandra Laffan] | # [mailto:claffan@myseneca.ca?subject=DPS921 Cassandra Laffan] | ||
| − | + | =Introduction= | |
| − | |||
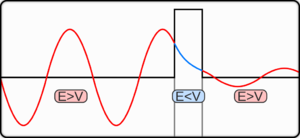
The concept of ''quantum tunneling'' is a subset of the Quantum Mechanics branch of theoretical physics. The core concept of Quantum Mechanics is that on a microscopic level, particles behave strangely, often in counter-intuitive ways. ''Quantum Tunneling'' refers to the phenomenon in which particles pass through barriers if the particles have enough energy and if the barrier is thin enough. In essence, said particles 'ignore' the barrier, continuing on as if nothing were there at all. | The concept of ''quantum tunneling'' is a subset of the Quantum Mechanics branch of theoretical physics. The core concept of Quantum Mechanics is that on a microscopic level, particles behave strangely, often in counter-intuitive ways. ''Quantum Tunneling'' refers to the phenomenon in which particles pass through barriers if the particles have enough energy and if the barrier is thin enough. In essence, said particles 'ignore' the barrier, continuing on as if nothing were there at all. | ||
[[File:TunnelEffektKling1.png|thumb| fig 1.1 Quantum tunnelling through a barrier. The energy of the tunnelled particle is the same but the probability amplitude is decreased.]] | [[File:TunnelEffektKling1.png|thumb| fig 1.1 Quantum tunnelling through a barrier. The energy of the tunnelled particle is the same but the probability amplitude is decreased.]] | ||
| − | + | ==Visualizing== | |
A good way to contrast quantum tunneling with intuition is to consider the following scenario: picture yourself at the bottom of a large hill. You have a tennis ball that you want to roll up the hill far enough that it rolls down the other side. If you don't give it enough energy to reach the top of the hill, the ball will merely roll back to you. | A good way to contrast quantum tunneling with intuition is to consider the following scenario: picture yourself at the bottom of a large hill. You have a tennis ball that you want to roll up the hill far enough that it rolls down the other side. If you don't give it enough energy to reach the top of the hill, the ball will merely roll back to you. | ||
| Line 19: | Line 20: | ||
| − | ==Program== | + | =OpenMP= |
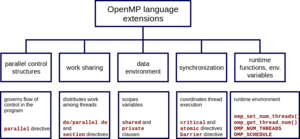
| − | + | [[File:OpenMP.png|thumb| fig 2.1 A chart of OpenMP constructs.]] | |
| − | [[File:FFT.png|thumb|fig | + | |
| − | [[File:FT.png|thumb|fig | + | OpenMP is a parallel programming API provided by Intel for C, C++, and Fortran. It enables flexible implementation of parallel algorithms, allowing computers of all builds to utilize all cores it has access to. |
| + | |||
| + | In this project, the <nowiki>#pragma omp parallel for</nowiki> statement was used in several locations in the program where for loops had no external dependencies. Where there were dependencies, math was used in such a way that the for loops no longer required the external variables. Their usage will be discussed further down. | ||
| + | |||
| + | =Program= | ||
| + | ==Without Parallel Processes== | ||
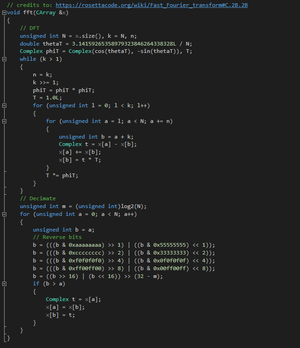
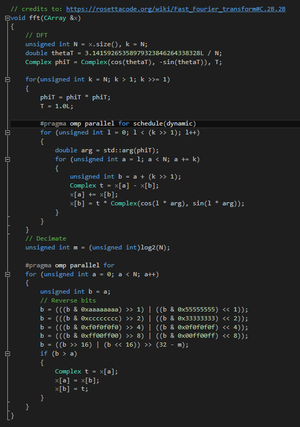
| + | [[File:FFT.png|thumb|fig 3.1 Fourier transformation code block.]] | ||
| + | [[File:FT.png|thumb|fig 3.2 Fourier transformations are called, in which the potential energy half step is calculated, then the full kinetic energy step, then finally the final potential energy half step.]] | ||
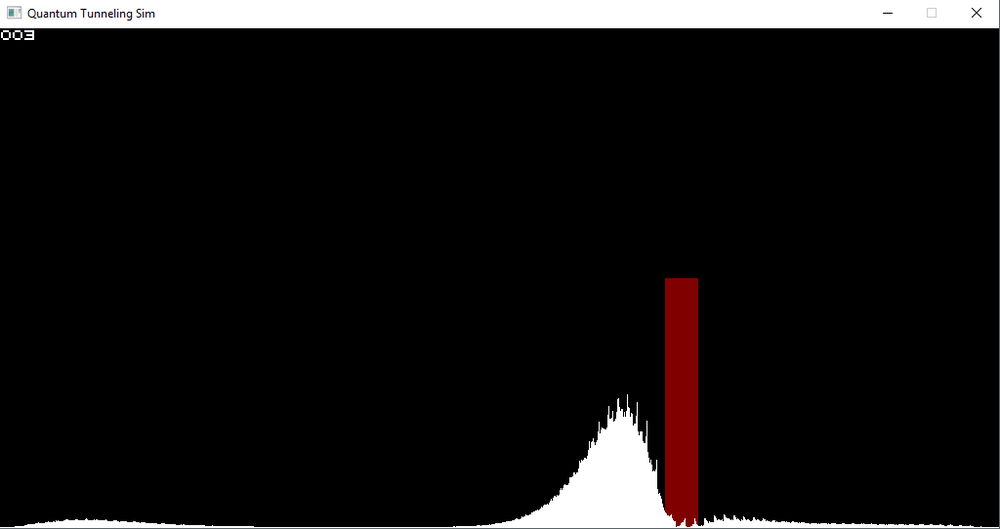
Originally, this program would calculate the path of a particle using Fourier transformations. These were used in place of the time resource consuming Schrodinger equations because the Schrodinger equations require the simulation to take into account, at each point: the potential energy after a half step, the kinetic energy after a whole step, then finally going back to take the potential energy of the half step. This was even more complicated because, for each particle, every neighboring particle had to be analyzed and accounted for as well. The Fourier transformations converted this into a simple process of multiplication, as shown in the code in figure 1.2: | Originally, this program would calculate the path of a particle using Fourier transformations. These were used in place of the time resource consuming Schrodinger equations because the Schrodinger equations require the simulation to take into account, at each point: the potential energy after a half step, the kinetic energy after a whole step, then finally going back to take the potential energy of the half step. This was even more complicated because, for each particle, every neighboring particle had to be analyzed and accounted for as well. The Fourier transformations converted this into a simple process of multiplication, as shown in the code in figure 1.2: | ||
| Line 33: | Line 41: | ||
| − | + | ==With Optimized Parallel Processes== | |
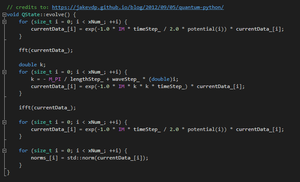
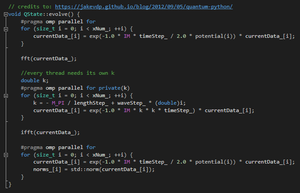
| − | [[File:PFFT.png|thumb|fig | + | [[File:PFFT.png|thumb|fig 4.1 Fourier transformation code block, with OpenMP parallelization.]] |
| − | [[File:PFT.png|thumb|fig | + | [[File:PFT.png|thumb|fig 4.2 Fourier transformations called in OpenMP.]] |
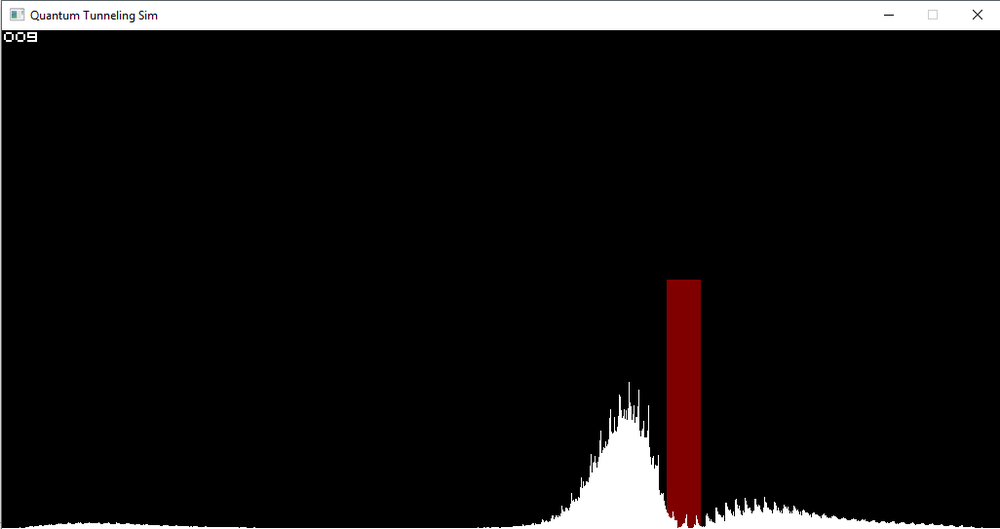
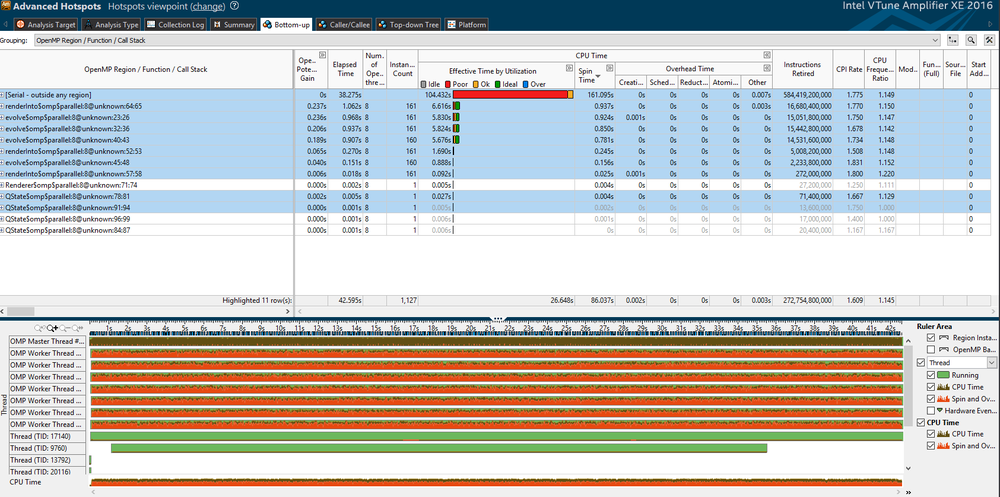
With the introduction of OpenMP into this project, several processes could be done in parallel. In the evolve() function, whenever a for loop was called, it could be parallelized because none of them had external variable dependencies. That eliminated quite a bit of overhead in the runtime. With the inclusion of OpenMP, the Fourier function, itself, was condensed substantially. This was achieved by introducing the Complex type into the program, so that complex calculations could be done in-line. The dynamic call to #pragma omp parallel also cut out a considerable amount of idle time that the CPU spent waiting to initialized all the threads that the program indicated that it required, rather than created threads on a need basis. | With the introduction of OpenMP into this project, several processes could be done in parallel. In the evolve() function, whenever a for loop was called, it could be parallelized because none of them had external variable dependencies. That eliminated quite a bit of overhead in the runtime. With the inclusion of OpenMP, the Fourier function, itself, was condensed substantially. This was achieved by introducing the Complex type into the program, so that complex calculations could be done in-line. The dynamic call to #pragma omp parallel also cut out a considerable amount of idle time that the CPU spent waiting to initialized all the threads that the program indicated that it required, rather than created threads on a need basis. | ||
| Line 44: | Line 52: | ||
| − | + | =Comparison and Analysis= | |
| + | ==Initial Performance== | ||
| + | |||
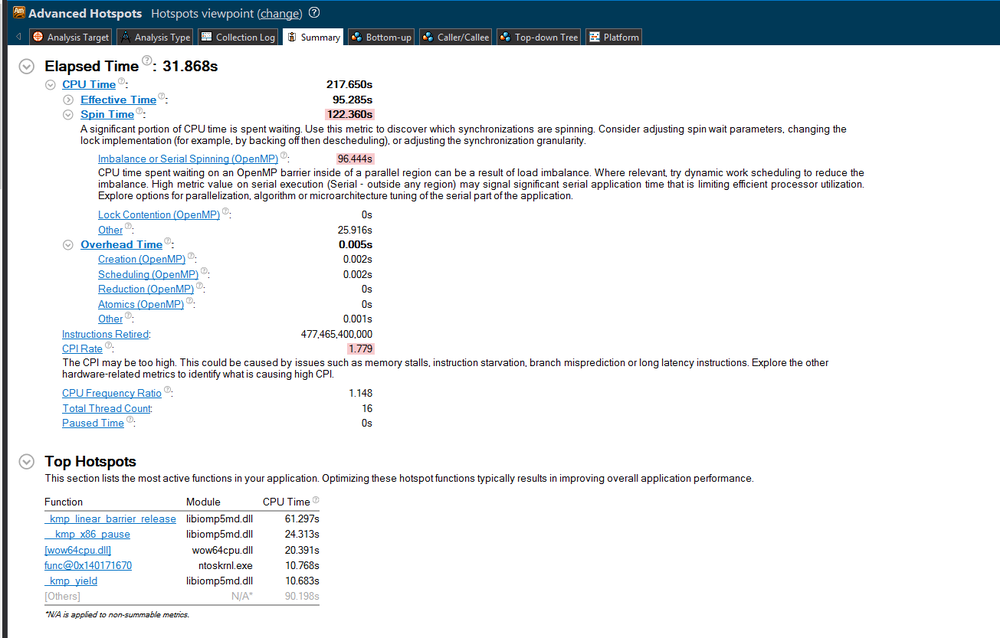
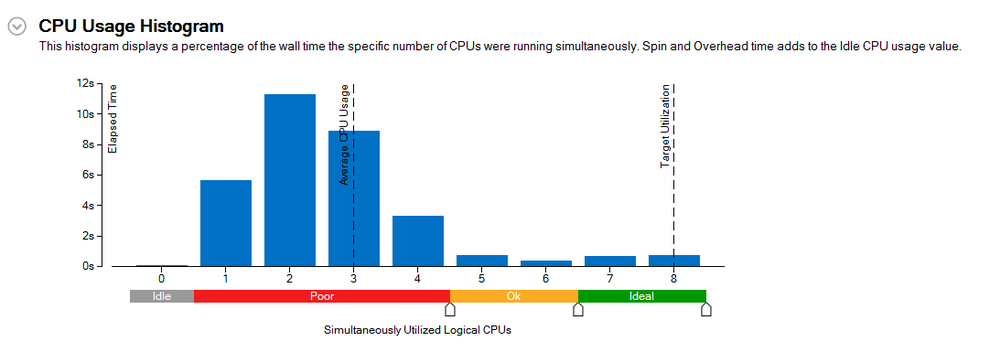
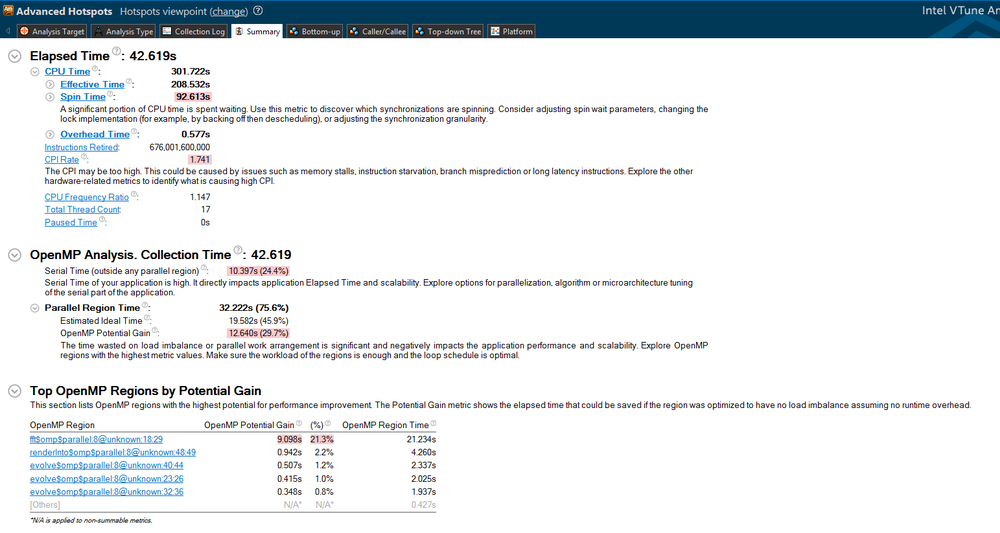
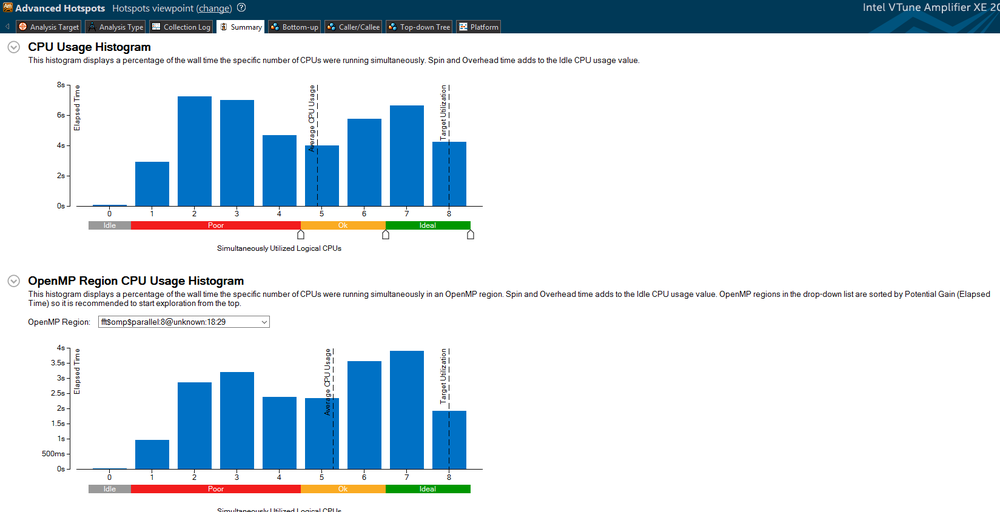
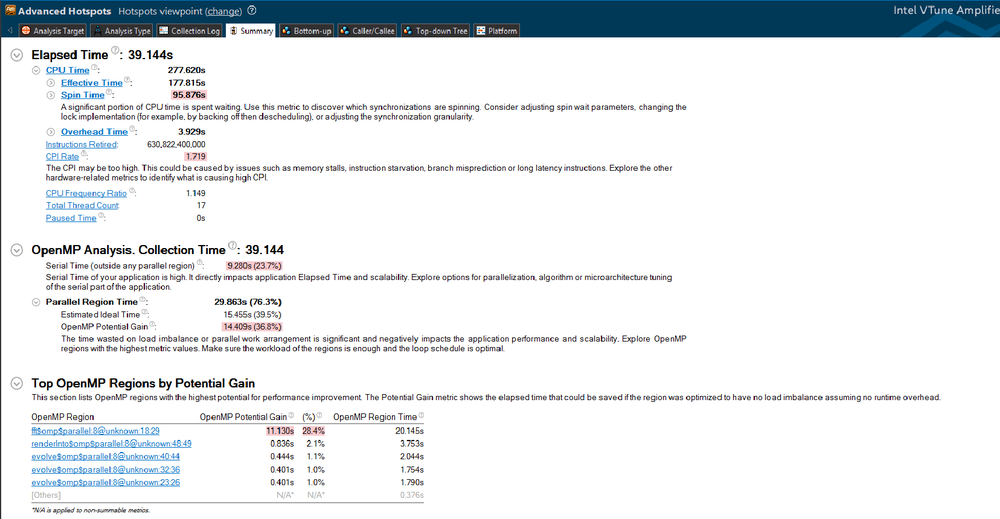
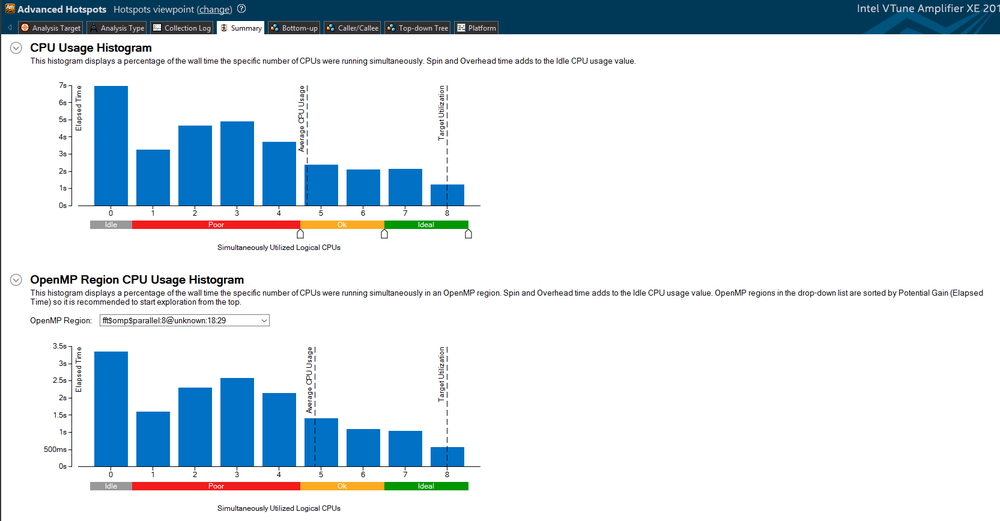
| + | Below, you can see the analysis provided by the VTune Amplifier, through visual studio. Here we can see the total elapsed time as well as the overhead time that the program used: | ||
[[File:initial_analysis.png|1000px|center|Initial performance ]] | [[File:initial_analysis.png|1000px|center|Initial performance ]] | ||
Revision as of 13:40, 21 December 2017
Contents
Simulating Quantum Tunneling With OpenMP
Members:
Introduction
The concept of quantum tunneling is a subset of the Quantum Mechanics branch of theoretical physics. The core concept of Quantum Mechanics is that on a microscopic level, particles behave strangely, often in counter-intuitive ways. Quantum Tunneling refers to the phenomenon in which particles pass through barriers if the particles have enough energy and if the barrier is thin enough. In essence, said particles 'ignore' the barrier, continuing on as if nothing were there at all.
Visualizing
A good way to contrast quantum tunneling with intuition is to consider the following scenario: picture yourself at the bottom of a large hill. You have a tennis ball that you want to roll up the hill far enough that it rolls down the other side. If you don't give it enough energy to reach the top of the hill, the ball will merely roll back to you.
Now replace the tennis ball with an electron. The electron, intuitively, would require a specific amount of energy needed to surpass a barrier, such as a gap of air. However, quantum mechanics and intuition tend not to occupy the same space! The electron, instead, always has a probability of passing through the barrier without ever having come in contact with the barrier in the first place. If this happens, the electron's probability will from there on out be lower than it was prior to tunneling through the barrier.
Keep in mind: this really only happens on the particle level, and not even to all particles. Only particles with low mass and high energy are capable of quantum tunneling, at least consistently.
OpenMP
OpenMP is a parallel programming API provided by Intel for C, C++, and Fortran. It enables flexible implementation of parallel algorithms, allowing computers of all builds to utilize all cores it has access to.
In this project, the #pragma omp parallel for statement was used in several locations in the program where for loops had no external dependencies. Where there were dependencies, math was used in such a way that the for loops no longer required the external variables. Their usage will be discussed further down.
Program
Without Parallel Processes
Originally, this program would calculate the path of a particle using Fourier transformations. These were used in place of the time resource consuming Schrodinger equations because the Schrodinger equations require the simulation to take into account, at each point: the potential energy after a half step, the kinetic energy after a whole step, then finally going back to take the potential energy of the half step. This was even more complicated because, for each particle, every neighboring particle had to be analyzed and accounted for as well. The Fourier transformations converted this into a simple process of multiplication, as shown in the code in figure 1.2:
After the values for all the particles' energies are calculated, they are rendered on the screen. Also rendered on the top left are the frames per second being rendered on the screen.
With Optimized Parallel Processes
With the introduction of OpenMP into this project, several processes could be done in parallel. In the evolve() function, whenever a for loop was called, it could be parallelized because none of them had external variable dependencies. That eliminated quite a bit of overhead in the runtime. With the inclusion of OpenMP, the Fourier function, itself, was condensed substantially. This was achieved by introducing the Complex type into the program, so that complex calculations could be done in-line. The dynamic call to #pragma omp parallel also cut out a considerable amount of idle time that the CPU spent waiting to initialized all the threads that the program indicated that it required, rather than created threads on a need basis.
On this screen, the parallelized version of this code is running. Observe that the framerate is considerably better than the non-OpenMP program.
Comparison and Analysis
Initial Performance
Below, you can see the analysis provided by the VTune Amplifier, through visual studio. Here we can see the total elapsed time as well as the overhead time that the program used: