Difference between revisions of "BETTERRED"

From CDOT Wiki
Jump to: navigation, search
(→‎Code)
 
(36 intermediate revisions by 3 users not shown)
Line 23: Line 23:
 
The program can then be executed by running the compiled binary and it will display the time it took to generate the Mandelbrot set and save the pictures.
 
The program can then be executed by running the compiled binary and it will display the time it took to generate the Mandelbrot set and save the pictures.
  
−
=== Observations ===
+
{| class="wikitable mw-collapsible mw-collapsed"
 +
! Mandelbrot CPU( ... )
 +
|-
 +
|
 +
<syntaxhighlight lang="cpp">
 +
#include <iostream>
 +
#include <complex>
 +
#include <vector>
 +
#include <chrono>
 +
#include <functional>
  
−
The program takes a significant amount of time to run as the calculations are being done on the CPU. There are nested loops present within the program that can be parallelized to make the program faster.
+
#include "window.h"
 +
#include "save_image.h"
 +
#include "utils.h"
  
−
The code also has the size of the image and the iterations hard-coded which can be modified to make the program significantly longer to process and make it tough on the GPU's for benchmarking and stability testing by running the process in a loop. The code is relatively straight forward and the parallelization should also be easy to implement and test.
+
// clang++ -std=c++11 -stdlib=libc++ -O3 save_image.cpp utils.cpp mandel.cpp -lfreeimage
  
 +
// Use an alias to simplify the use of complex type
 +
using Complex = std::complex<float>;
  
−
=== Hotspot ===
+
// Convert a pixel coordinate to the complex domain
 +
Complex scale(window<int> &scr, window<float> &fr, Complex c) {
 +
Complex aux(c.real() / (float)scr.width() * fr.width() + fr.x_min(),
 +
c.imag() / (float)scr.height() * fr.height() + fr.y_min());
 +
return aux;
 +
}
  
−
Hotspot for the program was found in the fractal() function which calls the get_iterations() function that contains 2-nested for loops and a call to escape() which contains a while loop. Profiling the runtime with Instruments on OSX displayed that the fractal() function took up the most amount of runtime and this is the function that will be parallelized using CUDA. Once the function is parallelized, the iterations and size of the image can be increased in order to make the computation relatively stressful on the GPU to get a benchmark or looped in order to do stress testing for GPUs.
+
// Check if a point is in the set or escapes to infinity, return the number if iterations
 +
int escape(Complex c, int iter_max, const std::function<Complex( Complex, Complex)> &func) {
 +
Complex z(0);
 +
int iter = 0;
  
 +
while (abs(z) < 2.0 && iter < iter_max) {
 +
z = func(z, c);
 +
iter++;
 +
}
 +
return iter;
 +
}
  
−
=== Profiling Data Screenshots ===
+
// Loop over each pixel from our image and check if the points associated with this pixel escape to infinity
 +
void get_number_iterations(window<int> &scr, window<float> &fract, int iter_max, std::vector<int> &colors,
 +
const std::function<Complex( Complex, Complex)> &func) {
 +
int k = 0, progress = -1;
 +
for(int i = scr.y_min(); i < scr.y_max(); ++i) {
 +
for(int j = scr.x_min(); j < scr.x_max(); ++j) {
 +
Complex c((float)j, (float)i);
 +
c = scale(scr, fract, c);
 +
colors[k] = escape(c, iter_max, func);
 +
k++;
 +
}
 +
if(progress < (int)(i*100.0/scr.y_max())){
 +
progress = (int)(i*100.0/scr.y_max());
 +
std::cout << progress << "%\n";
 +
}
 +
}
 +
}
  
−
Profile - [https://drive.google.com/open?id=0B2Y_atB3DptbUG5oRWMyUGNQdlU  Profile]
+
void fractal(window<int> &scr, window<float> &fract, int iter_max, std::vector<int> &colors,
 +
const std::function<Complex( Complex, Complex)> &func, const char *fname, bool smooth_color) {
 +
auto start = std::chrono::steady_clock::now();
 +
get_number_iterations(scr, fract, iter_max, colors, func);
 +
auto end = std::chrono::steady_clock::now();
 +
std::cout << "Time to generate " << fname << " = " << std::chrono::duration <float, std::milli> (end - start).count() << " [ms]" << std::endl;
  
−
Hotspot Code - [https://drive.google.com/open?id=0B2Y_atB3DptbRlhCUTNyeEFDbEk Hotspot Code]
+
// Save (show) the result as an image
 +
plot(scr, colors, iter_max, fname, smooth_color);
 +
}
  
−
----
+
void mandelbrot() {
 +
// Define the size of the image
 +
window<int> scr(0, 1000, 0, 1000);
 +
// The domain in which we test for points
 +
window<float> fract(-2.2, 1.2, -1.7, 1.7);
  
−
== Introduction : GPU Benchmarking/Testing for NBody : Joshua Kraitberg ==
+
// The function used to calculate the fractal
 +
auto func = [] (Complex z, Complex c) -> Complex {return z * z + c; };
  
−
This program uses Newtonian mechanics and a four-order symplectic Candy-Rozmus integration (a symplectic algorithm guarantees exact conservation of energy and angular momentum). The initial conditions are obtained from JPL Horizons, ahd constants (like masses, gravitational constant) are those recommended by the International Astronomical Union. The program currently does not take into account effects like general relativity, the non-spherical shapes of celestial objects, tidal effects on Earth, etc. It also does not take the 500 asteroids used by JPL Horizons into accound in its model of the Solar System.
+
int iter_max = 500;
 +
const char *fname = "mandelbrot.png";
 +
bool smooth_color = true;
 +
std::vector<int> colors(scr.size());
  
−
[https://github.com/fding/nbody Source]
+
// Experimental zoom (bugs ?). This will modify the fract window (the domain in which we calculate the fractal function)
 +
//zoom(1.0, -1.225, -1.22, 0.15, 0.16, fract); //Z2
 +
 +
fractal(scr, fract, iter_max, colors, func, fname, smooth_color);
 +
}
  
−
=== Compilation Instructions: ===
+
void triple_mandelbrot() {
 +
// Define the size of the image
 +
window<int> scr(0, 2000, 0, 2000);
 +
// The domain in which we test for points
 +
window<float> fract(-1.5, 1.5, -1.5, 1.5);
  
−
For Unix/Linux based systems:
+
// The function used to calculate the fractal
 +
auto func = [] (Complex z, Complex c) -> Complex {return z * z * z + c; };
  
−
    g++ -std=c++11 c++/nbody.cpp
+
int iter_max = 500;
 +
const char *fname = "triple_mandelbrot.png";
 +
bool smooth_color = true;
 +
std::vector<int> colors(scr.size());
 +
 
 +
fractal(scr, fract, iter_max, colors, func, fname, smooth_color);
 +
}
 +
 
 +
int main() {
 +
 
 +
mandelbrot();
 +
// triple_mandelbrot();
 +
 
 +
return 0;
 +
}
 +
 
 +
</syntaxhighlight>
 +
|}
  
 
=== Observations ===
 
=== Observations ===
  
−
The program is quite fast for being a single-threaded CPU application. Almost all the CPU time is spent manipulating data and iterating in vectors.
+
The program takes a significant amount of time to run as the calculations are being done on the CPU. There are nested loops present within the program that can be parallelized to make the program faster.
 +
 
 +
The code also has the size of the image and the iterations hard-coded which can be modified to make the program significantly longer to process and make it tough on the GPU's for benchmarking and stability testing by running the process in a loop. The code is relatively straight forward and the parallelization should also be easy to implement and test.
 +
 
  
 
=== Hotspot ===
 
=== Hotspot ===
  
−
Essentially all the time spent running is spent in the doing calculation on vectors.  The dowork function iteratively calls the CRO_step function found in integrators.h file.  The CRO_step function is where most of the vector calculations take place. A large amount of is also done in the calculate_a function which is used to calulate the acceleration on all the planets.
+
Hotspot for the program was found in the fractal() function which calls the get_iterations() function that contains 2-nested for loops and a call to escape() which contains a while loop. Profiling the runtime with Instruments on OSX displayed that the fractal() function took up the most amount of runtime and this is the function that will be parallelized using CUDA. Once the function is parallelized, the iterations and size of the image can be increased in order to make the computation relatively stressful on the GPU to get a benchmark or looped in order to do stress testing for GPUs.
  
−
=== Profiling Data and Screenshots ===
 
  
−
{| class="wikitable mw-collapsible mw-collapsed"
+
=== Profiling Data Screenshots ===
−
! NBody Hot Functions
 
−
|-
 
−
|
 
  
−
<syntaxhighlight lang="cpp">
+
Profile - [https://drive.google.com/open?id=0B2Y_atB3DptbUG5oRWMyUGNQdlU Profile]
−
void dowork(double t){
 
−
int numtimes=int(abs(t/dt));
 
−
dt=t/double(numtimes+1);
 
−
numtimes=numtimes+1;
 
−
for (int i=0;i<numtimes;i++){
 
−
CRO_step(dt,a);
 
−
}
 
−
}  
 
  
−
void CRO_step(register double mydt,void (*a)()){
+
Hotspot Code - [https://drive.google.com/open?id=0B2Y_atB3DptbRlhCUTNyeEFDbEk Hotspot Code]
−
long double macr_a[4] = {0.5153528374311229364, -0.085782019412973646,0.4415830236164665242, 0.1288461583653841854};
 
−
long double macr_b[4] = {0.1344961992774310892, -0.2248198030794208058, 0.7563200005156682911, 0.3340036032863214255};
 
−
for (int i=0;i<4;i++){
 
−
            a();
 
−
            for (int j=0;j<ncobjects;j++){
 
−
                cobjects[j]->v +=  cobjects[j]->a * mydt*macr_b[i];
 
−
                cobjects[j]->pos += cobjects[j]->v  * mydt*macr_a[i];
 
−
}
 
−
} //We should really expand the loop for efficiency
 
−
} 
 
  
−
void calculate_a(){
+
----
−
for (int j1=0;j1<ncobjects;j1++){
 
−
cobjects[j1]->a=vect(0,0,0);
 
−
}
 
−
for (int j1=0; j1<ncobjects;j1++){
 
−
for (int j2=j1+1;j2<ncobjects;j2++){
 
−
double m1=cobjects[j1]->m;
 
−
double m2=cobjects[j2]->m;
 
−
vect dist=cobjects[j1]->pos-cobjects[j2]->pos;
 
−
double magd=dist.mag();
 
−
vect base=dist*(1.0/(magd*magd*magd));
 
−
cobjects[j1]->a+=base*(-m2);
 
−
cobjects[j2]->a+=base*m1;
 
−
}
 
−
}
 
−
}
 
−
</syntaxhighlight>
 
  
−
|}
+
== Introduction : GPU Benchmarking/Testing for NBody : Joshua Kraitberg ==
  
−
{| class="wikitable mw-collapsible mw-collapsed"
+
This program uses Newtonian mechanics and a four-order symplectic Candy-Rozmus integration (a symplectic algorithm guarantees exact conservation of energy and angular momentum). The initial conditions are obtained from JPL Horizons, ahd constants (like masses, gravitational constant) are those recommended by the International Astronomical Union. The program currently does not take into account effects like general relativity, the non-spherical shapes of celestial objects, tidal effects on Earth, etc. It also does not take the 500 asteroids used by JPL Horizons into accound in its model of the Solar System.
−
! NBody Hot Spot Data
+
 
−
|-
+
[https://github.com/fding/nbody Source]
−
|     Call graph (explanation follows)
+
 
 +
=== Compilation Instructions: ===
 +
 
 +
For Unix/Linux based systems:
 +
 
 +
    g++ -std=c++11 c++/nbody.cpp
 +
 
 +
=== Observations ===
 +
 
 +
The program is quite fast for being a single-threaded CPU application.  Almost all the CPU time is spent manipulating data and iterating in vectors.
 +
 
 +
=== Hotspot ===
  
 +
Essentially all the time spent running is spent in the doing calculation on vectors.  The dowork function iteratively calls the CRO_step function found in integrators.h file.  The CRO_step function is where most of the vector calculations take place.  A large amount of is also done in the calculate_a function which is used to calulate the acceleration on all the planets.
  
−
granularity: each sample hit covers 4 byte(s) for 0.16% of 6.18 seconds
+
=== Profiling Data and Screenshots ===
  
−
index % time    self  children    called    name
+
{| class="wikitable mw-collapsible mw-collapsed"
−
                                                <spontaneous>
+
! NBody Hot Functions
−
[1]    99.7    0.00    6.16                main [1]
+
|-
−
                0.00    6.15      1/1           dowork(double) [3]
+
|
−
                0.00    0.01      1/1          totalL() [14]
+
 
−
                0.00    0.00      1/1          totalE() [16]
+
<syntaxhighlight lang="cpp">
−
                0.00    0.00      1/1          initialize() [17]
+
void dowork(double t){
−
                0.00    0.00      28/32712799    vect::operator-(vect const&) [8]
+
int numtimes=int(abs(t/dt));
−
                0.00    0.00      14/118268959    vect::operator*(double const&) [5]
+
dt=t/double(numtimes+1);
−
                0.00    0.00      14/5032775    vect::operator=(vect const&) [11]
+
numtimes=numtimes+1;
−
                0.00    0.00      42/42          std::vector<int, std::allocator<int> >::operator[](unsigned int) [22]
+
for (int i=0;i<numtimes;i++){
−
                0.00    0.00      16/16          bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*) [33]
+
CRO_step(dt,a);
−
                0.00    0.00      15/35          std::vector<int, std::allocator<int> >::size() const [23]
+
}
−
                0.00    0.00      14/14          std::vector<int, std::allocator<int> >::push_back(int const&) [39]
+
} 
−
                0.00    0.00      14/14          getobj(int) [36]
+
 
−
                0.00    0.00      3/3          std::vector<double, std::allocator<double> >::operator[](unsigned int) [90]
+
void CRO_step(register double mydt,void (*a)()){
−
                0.00    0.00      2/2          print_hline() [94]
+
long double macr_a[4] = {0.5153528374311229364, -0.085782019412973646,0.4415830236164665242, 0.1288461583653841854};
−
                0.00    0.00      2/10          std::vector<double, std::allocator<double> >::size() const [45]
+
long double macr_b[4] = {0.1344961992774310892, -0.2248198030794208058, 0.7563200005156682911, 0.3340036032863214255};
−
                0.00   0.00       1/1           std::ios_base::precision(int) [146]
+
for (int i=0;i<4;i++){
−
                 0.00    0.00       1/1          std::vector<double, std::allocator<double> >::vector() [142]
+
            a();
−
                 0.00    0.00       1/1          std::vector<int, std::allocator<int> >::vector() [144]
+
            for (int j=0;j<ncobjects;j++){
−
                 0.00    0.00      1/1          std::vector<double, std::allocator<double> >::push_back(double const&) [141]
+
                cobjects[j]->v +=  cobjects[j]->a * mydt*macr_b[i];
−
                 0.00    0.00      1/1          std::vector<std::string, std::allocator<std::string> >::vector() [135]
+
                cobjects[j]->pos += cobjects[j]->v  * mydt*macr_a[i];
−
                 0.00    0.00       1/1          std::vector<std::string, std::allocator<std::string> >::~vector() [136]
+
}
−
                 0.00    0.00       1/1          JD(tm*) [103]
+
} //We should really expand the loop for efficiency
−
                 0.00    0.00       1/1          std::vector<double, std::allocator<double> >::push_back(double&&) [140]
+
} 
−
                 0.00    0.00       1/1          std::vector<int, std::allocator<int> >::~vector() [145]
+
 
−
                 0.00    0.00       1/1          std::vector<double, std::allocator<double> >::~vector() [143]
+
void calculate_a(){
−
-----------------------------------------------
+
for (int j1=0;j1<ncobjects;j1++){
−
                0.14    6.01  89870/89870      dowork(double) [3]
+
cobjects[j1]->a=vect(0,0,0);
−
[2]    99.6   0.14   6.01  89870        CRO_step(double, void (*)()) [2]
+
}
−
                 1.18   4.22  359480/359480      calculate_a() [4]
+
for (int j1=0; j1<ncobjects;j1++){
−
                 0.20   0.29 20130880/118268959    vect::operator*(double const&) [5]
+
for (int j2=j1+1;j2<ncobjects;j2++){
−
                 0.12   0.00 10065440/75490814    vect::operator+=(vect const&) [7]
+
double m1=cobjects[j1]->m;
−
-----------------------------------------------
+
double m2=cobjects[j2]->m;
−
                 0.00    6.15       1/1          main [1]
+
vect dist=cobjects[j1]->pos-cobjects[j2]->pos;
−
[3]    99.6   0.00   6.15       1         dowork(double) [3]
+
double magd=dist.mag();
−
                 0.14   6.01  89870/89870      CRO_step(double, void (*)()) [2]
+
vect base=dist*(1.0/(magd*magd*magd));
−
                 0.00    0.00      1/1          std::abs(double) [147]
+
cobjects[j1]->a+=base*(-m2);
−
-----------------------------------------------
+
cobjects[j2]->a+=base*m1;
−
                 1.18   4.22  359480/359480      CRO_step(double, void (*)()) [2]
+
}
−
[4]    87.5   1.18    4.22  359480        calculate_a() [4]
+
}
−
                 1.00    1.39 98138040/118268959    vect::operator*(double const&) [5]
+
}
−
                 0.78   0.00 65425360/75490814    vect::operator+=(vect const&) [7]
+
</syntaxhighlight>
−
                 0.26   0.37 32712680/32712799    vect::operator-(vect const&) [8]
+
 
−
                0.32    0.00 32712680/32712785    vect::mag() [10]
+
|}
−
                0.08    0.00 5032720/5032775    vect::operator=(vect const&) [11]
+
 
−
                0.01    0.00 5032720/5032775    vect::vect(double, double, double) [13]
+
{| class="wikitable mw-collapsible mw-collapsed"
−
-----------------------------------------------
+
! NBody Hot Spot Data
−
                0.00    0.00      11/118268959    initialize() [17]
+
|-
−
                0.00    0.00      14/118268959    main [1]
+
|     Call graph (explanation follows)
−
                0.00    0.00      14/118268959    totalL() [14]
+
 
−
                0.20    0.29 20130880/118268959    CRO_step(double, void (*)()) [2]
+
 
−
                1.00    1.39 98138040/118268959    calculate_a() [4]
+
granularity: each sample hit covers 4 byte(s) for 0.16% of 6.18 seconds
−
[5]    46.5    1.20    1.67 118268959        vect::operator*(double const&) [5]
+
 
−
                1.67    0.00 118268959/118268959    vect::operator*=(double const&) [6]
+
index % time    self  children    called    name
−
-----------------------------------------------
+
                                                <spontaneous>
−
                1.67    0.00 118268959/118268959    vect::operator*(double const&) [5]
+
[1]     99.7   0.00   6.16                main [1]
−
[6]    27.1    1.67    0.00 118268959        vect::operator*=(double const&) [6]
+
                 0.00    6.15       1/1          dowork(double) [3]
−
-----------------------------------------------
+
                 0.00    0.01       1/1          totalL() [14]
−
                0.00    0.00      14/75490814    totalL() [14]
+
                 0.00    0.00      1/1          totalE() [16]
−
                0.12    0.00 10065440/75490814    CRO_step(double, void (*)()) [2]
+
                 0.00    0.00      1/1          initialize() [17]
−
                0.78    0.00 65425360/75490814    calculate_a() [4]
+
                 0.00    0.00     28/32712799    vect::operator-(vect const&) [8]
−
[7]    14.6    0.91    0.00 75490814        vect::operator+=(vect const&) [7]
+
                 0.00    0.00     14/118268959    vect::operator*(double const&) [5]
−
-----------------------------------------------
+
                 0.00    0.00     14/5032775    vect::operator=(vect const&) [11]
−
                0.00    0.00      28/32712799    main [1]
+
                 0.00    0.00     42/42          std::vector<int, std::allocator<int> >::operator[](unsigned int) [22]
−
                0.00    0.00      91/32712799    totalE() [16]
+
                 0.00    0.00     16/16          bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*) [33]
−
                0.26    0.37 32712680/32712799    calculate_a() [4]
+
                0.00    0.00      15/35          std::vector<int, std::allocator<int> >::size() const [23]
−
[8]    10.4    0.27    0.38 32712799        vect::operator-(vect const&) [8]
+
                0.00   0.00      14/14         std::vector<int, std::allocator<int> >::push_back(int const&) [39]
−
                0.38    0.00 32712799/32712799    vect::operator-=(vect const&) [9]
+
                 0.00   0.00      14/14          getobj(int) [36]
−
-----------------------------------------------
+
                 0.00   0.00      3/3          std::vector<double, std::allocator<double> >::operator[](unsigned int) [90]
−
                0.38    0.00 32712799/32712799    vect::operator-(vect const&) [8]
+
                 0.00   0.00       2/2          print_hline() [94]
−
[9]      6.1    0.38    0.00 32712799        vect::operator-=(vect const&) [9]
+
                0.00    0.00      2/10          std::vector<double, std::allocator<double> >::size() const [45]
−
-----------------------------------------------
+
                 0.00    0.00       1/1          std::ios_base::precision(int) [146]
−
                0.00    0.00    105/32712785    totalE() [16]
+
                0.00   0.00      1/1          std::vector<double, std::allocator<double> >::vector() [142]
−
                0.32    0.00 32712680/32712785    calculate_a() [4]
+
                 0.00   0.00      1/1          std::vector<int, std::allocator<int> >::vector() [144]
−
[10]    5.2    0.32    0.00 32712785        vect::mag() [10]
+
                 0.00    0.00      1/1          std::vector<double, std::allocator<double> >::push_back(double const&) [141]
 +
                0.00    0.00      1/1          std::vector<std::string, std::allocator<std::string> >::vector() [135]
 +
                 0.00   0.00      1/1          std::vector<std::string, std::allocator<std::string> >::~vector() [136]
 +
                0.00   0.00      1/1          JD(tm*) [103]
 +
                 0.00    0.00      1/1          std::vector<double, std::allocator<double> >::push_back(double&&) [140]
 +
                 0.00   0.00       1/1          std::vector<int, std::allocator<int> >::~vector() [145]
 +
                 0.00   0.00      1/1          std::vector<double, std::allocator<double> >::~vector() [143]
 
-----------------------------------------------
 
-----------------------------------------------
−
                 0.00   0.00      14/5032775    main [1]
+
                 0.14    6.01  89870/89870      dowork(double) [3]
−
                 0.00   0.00     41/5032775    initialize() [17]
+
[2]    99.6   0.14   6.01  89870        CRO_step(double, void (*)()) [2]
−
                 0.08   0.00 5032720/5032775     calculate_a() [4]
+
                 1.18   4.22  359480/359480     calculate_a() [4]
−
[11]    1.4    0.08   0.00 5032775        vect::operator=(vect const&) [11]
+
                 0.20   0.29 20130880/118268959     vect::operator*(double const&) [5]
 +
                0.12   0.00 10065440/75490814    vect::operator+=(vect const&) [7]
 
-----------------------------------------------
 
-----------------------------------------------
−
                                                <spontaneous>
+
                0.00    6.15      1/1          main [1]
−
[12]    0.3    0.02   0.00                 vect::operator+(vect const&) [12]
+
[3]    99.6    0.00    6.15      1        dowork(double) [3]
 +
                0.14   6.01  89870/89870      CRO_step(double, void (*)()) [2]
 +
                0.00   0.00       1/1          std::abs(double) [147]
 
-----------------------------------------------
 
-----------------------------------------------
−
                 0.00   0.00     14/5032775     cross(vect const&, vect const&) [15]
+
                1.18    4.22  359480/359480      CRO_step(double, void (*)()) [2]
−
                 0.00   0.00     41/5032775     initialize() [17]
+
[4]    87.5    1.18    4.22  359480        calculate_a() [4]
−
                 0.01   0.00 5032720/5032775    calculate_a() [4]
+
                1.00    1.39 98138040/118268959    vect::operator*(double const&) [5]
−
[13]    0.2    0.01    0.00 5032775         vect::vect(double, double, double) [13]
+
                 0.78   0.00 65425360/75490814     vect::operator+=(vect const&) [7]
 +
                0.26    0.37 32712680/32712799    vect::operator-(vect const&) [8]
 +
                 0.32   0.00 32712680/32712785     vect::mag() [10]
 +
                 0.08   0.00 5032720/5032775    vect::operator=(vect const&) [11]
 +
                0.01    0.00 5032720/5032775     vect::vect(double, double, double) [13]
 
-----------------------------------------------
 
-----------------------------------------------
−
                 0.00    0.01      1/1          main [1]
+
                 0.00    0.00      11/118268959    initialize() [17]
−
[14]    0.1   0.00   0.01      1         totalL() [14]
+
                0.00   0.00     14/118268959    main [1]
−
                 0.01   0.00      14/14          cross(vect const&, vect const&) [15]
+
                 0.00   0.00      14/118268959    totalL() [14]
−
                 0.00   0.00      14/118268959    vect::operator*(double const&) [5]
+
                 0.20   0.29 20130880/118268959    CRO_step(double, void (*)()) [2]
−
                 0.00    0.00      14/75490814     vect::operator+=(vect const&) [7]
+
                 1.00    1.39 98138040/118268959    calculate_a() [4]
−
                 0.00   0.00       1/85          vect::vect() [21]
+
[5]     46.5    1.20    1.67 118268959        vect::operator*(double const&) [5]
 +
                 1.67   0.00 118268959/118268959    vect::operator*=(double const&) [6]
 
-----------------------------------------------
 
-----------------------------------------------
−
                 0.01   0.00      14/14          totalL() [14]
+
                1.67    0.00 118268959/118268959    vect::operator*(double const&) [5]
−
[15]    0.1   0.01   0.00      14         cross(vect const&, vect const&) [15]
+
[6]    27.1    1.67    0.00 118268959        vect::operator*=(double const&) [6]
−
                 0.00   0.00     14/5032775     vect::vect(double, double, double) [13]
+
-----------------------------------------------
−
|}
+
                 0.00   0.00      14/75490814    totalL() [14]
−
 
+
                0.12    0.00 10065440/75490814    CRO_step(double, void (*)()) [2]
−
{| class="wikitable mw-collapsible mw-collapsed"
+
                0.78    0.00 65425360/75490814    calculate_a() [4]
−
! NBody gprof Complete Data (Warning: long)
+
[7]    14.6    0.91    0.00 75490814        vect::operator+=(vect const&) [7]
−
|-
+
-----------------------------------------------
−
|     Call graph (explanation follows)
+
                0.00    0.00      28/32712799    main [1]
−
 
+
                0.00   0.00      91/32712799    totalE() [16]
−
 
+
                0.26    0.37 32712680/32712799    calculate_a() [4]
−
granularity: each sample hit covers 4 byte(s) for 0.16% of 6.18 seconds
+
[8]    10.4    0.27    0.38 32712799         vect::operator-(vect const&) [8]
−
 
+
                0.38    0.00 32712799/32712799    vect::operator-=(vect const&) [9]
−
index % time   self  children   called    name
+
-----------------------------------------------
−
                                                 <spontaneous>
+
                 0.38   0.00 32712799/32712799     vect::operator-(vect const&) [8]
−
[1]    99.7   0.00   6.16                 main [1]
+
[9]      6.1    0.38    0.00 32712799        vect::operator-=(vect const&) [9]
−
                 0.00    6.15      1/1          dowork(double) [3]
+
-----------------------------------------------
−
                 0.00    0.01      1/1          totalL() [14]
+
                0.00    0.00    105/32712785    totalE() [16]
−
                 0.00    0.00       1/1          totalE() [16]
+
                0.32    0.00 32712680/32712785    calculate_a() [4]
−
                 0.00    0.00       1/1          initialize() [17]
+
[10]    5.2    0.32    0.00 32712785        vect::mag() [10]
−
                 0.00   0.00      28/32712799    vect::operator-(vect const&) [8]
+
-----------------------------------------------
 +
                0.00    0.00      14/5032775    main [1]
 +
                0.00    0.00      41/5032775    initialize() [17]
 +
                0.08    0.00 5032720/5032775    calculate_a() [4]
 +
[11]    1.4   0.08   0.00 5032775        vect::operator=(vect const&) [11]
 +
-----------------------------------------------
 +
                                                 <spontaneous>
 +
[12]    0.3   0.02   0.00                 vect::operator+(vect const&) [12]
 +
-----------------------------------------------
 +
                 0.00    0.00      14/5032775    cross(vect const&, vect const&) [15]
 +
                 0.00    0.00      41/5032775    initialize() [17]
 +
                 0.01    0.00 5032720/5032775    calculate_a() [4]
 +
[13]    0.2    0.01   0.00 5032775        vect::vect(double, double, double) [13]
 +
-----------------------------------------------
 +
                 0.00    0.01       1/1          main [1]
 +
[14]    0.1    0.00    0.01      1        totalL() [14]
 +
                 0.01   0.00      14/14          cross(vect const&, vect const&) [15]
 
                 0.00    0.00      14/118268959    vect::operator*(double const&) [5]
 
                 0.00    0.00      14/118268959    vect::operator*(double const&) [5]
−
                 0.00    0.00      14/5032775    vect::operator=(vect const&) [11]
+
                0.00    0.00      14/75490814    vect::operator+=(vect const&) [7]
−
                 0.00    0.00      42/42          std::vector<int, std::allocator<int> >::operator[](unsigned int) [22]
+
                0.00    0.00      1/85          vect::vect() [21]
−
                 0.00    0.00      16/16          bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*) [33]
+
-----------------------------------------------
−
                 0.00    0.00      15/35          std::vector<int, std::allocator<int> >::size() const [23]
+
                0.01    0.00      14/14          totalL() [14]
−
                 0.00    0.00      14/14          std::vector<int, std::allocator<int> >::push_back(int const&) [39]
+
[15]    0.1    0.01    0.00      14        cross(vect const&, vect const&) [15]
−
                 0.00    0.00      14/14          getobj(int) [36]
+
                0.00    0.00      14/5032775    vect::vect(double, double, double) [13]
−
                 0.00    0.00      3/3          std::vector<double, std::allocator<double> >::operator[](unsigned int) [90]
+
|}
 +
 
 +
{| class="wikitable mw-collapsible mw-collapsed"
 +
! NBody gprof Complete Data (Warning: long)
 +
|-
 +
|     Call graph (explanation follows)
 +
 
 +
 
 +
granularity: each sample hit covers 4 byte(s) for 0.16% of 6.18 seconds
 +
 
 +
index % time    self  children    called    name
 +
                                                <spontaneous>
 +
[1]    99.7    0.00    6.16                main [1]
 +
                0.00    6.15      1/1          dowork(double) [3]
 +
                0.00    0.01      1/1          totalL() [14]
 +
                0.00    0.00      1/1          totalE() [16]
 +
                0.00    0.00      1/1          initialize() [17]
 +
                0.00    0.00      28/32712799    vect::operator-(vect const&) [8]
 +
                0.00    0.00      14/118268959    vect::operator*(double const&) [5]
 +
                 0.00    0.00      14/5032775    vect::operator=(vect const&) [11]
 +
                 0.00    0.00      42/42          std::vector<int, std::allocator<int> >::operator[](unsigned int) [22]
 +
                 0.00    0.00      16/16          bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*) [33]
 +
                 0.00    0.00      15/35          std::vector<int, std::allocator<int> >::size() const [23]
 +
                 0.00    0.00      14/14          std::vector<int, std::allocator<int> >::push_back(int const&) [39]
 +
                 0.00    0.00      14/14          getobj(int) [36]
 +
                 0.00    0.00      3/3          std::vector<double, std::allocator<double> >::operator[](unsigned int) [90]
 
                 0.00    0.00      2/2          print_hline() [94]
 
                 0.00    0.00      2/2          print_hline() [94]
 
                 0.00    0.00      2/10          std::vector<double, std::allocator<double> >::size() const [45]
 
                 0.00    0.00      2/10          std::vector<double, std::allocator<double> >::size() const [45]
Line 1,103: Line 1,219:
  
 
An even better way would be to integrate the Gaussian function instead of just taking point samples. Refer to the two graphs on the right.<br/>
 
An even better way would be to integrate the Gaussian function instead of just taking point samples. Refer to the two graphs on the right.<br/>
−
The graphs plot the continuous distribution function and the discrete kernel approximation. One thing to look out for are the tails of the distribution vs. kernel support:<br/>
+
The graphs plot the continuous distribution function and the discrete kernel approximation. One thing to look out for are the tails of the distribution vs. kernel weight:<br/>
 
For the current configuration, we have 13.36% of the curve’s area outside the discrete kernel. Note that the weights are renormalized such that the sum of all weights is one. Or in other words:<br/>
 
For the current configuration, we have 13.36% of the curve’s area outside the discrete kernel. Note that the weights are renormalized such that the sum of all weights is one. Or in other words:<br/>
 
the probability mass outside the discrete kernel is redistributed evenly to all pixels within the kernel. The weights are calculated by numerical integration of the continuous gaussian distribution<br/>
 
the probability mass outside the discrete kernel is redistributed evenly to all pixels within the kernel. The weights are calculated by numerical integration of the continuous gaussian distribution<br/>
Line 1,682: Line 1,798:
 
   char *destFileName = argv[2];
 
   char *destFileName = argv[2];
  
−
#endif /* RUN_GROF */
+
#endif /* RUN_GPROF */
  
 
   if (showUsage)
 
   if (showUsage)
Line 1,782: Line 1,898:
 
To compile and run the program:
 
To compile and run the program:
 
# Navigate to the directory you want to run the program in.
 
# Navigate to the directory you want to run the program in.
−
# Save [http://matrix.senecac.on.ca/~cpaul12/cinque_terre.bmp this] image and place it directory you will be running the program from.  
+
# Save [http://matrix.senecac.on.ca/~cpaul12/cinque_terre.bmp this] image and place it into the directory you will be running the program from.  
 
# Copy the Linux version of the main source code above and paste it into a [your chosen file name].cpp file.
 
# Copy the Linux version of the main source code above and paste it into a [your chosen file name].cpp file.
 
# Copy the Linux version of the header source code above and paste it into a file named windows.h.
 
# Copy the Linux version of the header source code above and paste it into a file named windows.h.
Line 1,795: Line 1,911:
 
To compile and run the program:
 
To compile and run the program:
 
# Navigate to the directory you want to run the program in.
 
# Navigate to the directory you want to run the program in.
−
# Save [http://matrix.senecac.on.ca/~cpaul12/cinque_terre.bmp this] image and place it directory you will be running the program from.  
+
# Save [http://matrix.senecac.on.ca/~cpaul12/cinque_terre.bmp this] image and place it into the directory you will be running the program from.  
 
# Copy the Linux version of the main source code above and paste it into a [your chosen file name].cpp file.
 
# Copy the Linux version of the main source code above and paste it into a [your chosen file name].cpp file.
 
# Copy the Linux version of the header source code above and paste it into a file named windows.h.
 
# Copy the Linux version of the header source code above and paste it into a file named windows.h.
Line 1,940: Line 2,056:
 
for parallelization using CUDA. The sigma (&sigma;) and the kernel size can be increased in order to make the computation stressful on the GPU to get a significant benchmark.
 
for parallelization using CUDA. The sigma (&sigma;) and the kernel size can be increased in order to make the computation stressful on the GPU to get a significant benchmark.
  
−
= Assignment 2 - Parallelize =
+
= Assignment 2/3 - Parallelize & Optimize =
 +
&#42; For gaussian blur we say it's unoptimized because we feel that there is more that can be done to reduce the execution times.<br/>
 +
&nbsp;&nbsp;The code displayed in the code snippets does use CUDA parallel constructs and fine tuning techniques such as streaming - async.
 +
== Gaussian Blur ==
  
 
{| class="wikitable mw-collapsible mw-collapsed"
 
{| class="wikitable mw-collapsible mw-collapsed"
−
! Culptit - BlurImage( ... )
+
! Unoptimized* - BlurImage( ... )
 
|-
 
|-
 
|
 
|
Line 1,956: Line 2,075:
 
#include <windows.h>  // for bitmap headers.
 
#include <windows.h>  // for bitmap headers.
 
#include <algorithm>
 
#include <algorithm>
 +
#include <chrono>
  
 
#include <cuda_runtime.h>
 
#include <cuda_runtime.h>
Line 1,962: Line 2,082:
 
#include <device_functions.h>
 
#include <device_functions.h>
  
−
//#if defined(__NVCC__) && __CUDACC_VER_MAJOR__ != 1
+
//#ifdef __CUDACC__
−
const int ntpb = 1024;
+
//#if __CUDACC_VER_MAJOR__ == 1
−
//#elif defined(__NVCC__) &&__CUDACC_VER_MAJOR__ == 1
 
 
//const int ntpb = 512;
 
//const int ntpb = 512;
 +
//#else
 +
//const int ntpb = 1024;
 +
//#endif
 
//#endif
 
//#endif
−
 
+
const int ntpb = 1024;
−
const float c_pi = 3.14159265359f;
+
const int STREAMS = 32;
  
 
void check(cudaError_t error) {
 
void check(cudaError_t error) {
Line 2,118: Line 2,240:
 
}
 
}
  
−
const uint8_t* GetPixelOrBlack(const SImageData& image, int x, int y)
+
struct BGRPixel {
−
{
+
float b;
−
static const uint8_t black[3] = { 0, 0, 0 };
+
float g;
−
if (x < 0 || x >= image.m_width ||
+
float r;
−
y < 0 || y >= image.m_height)
+
};
−
{
 
−
return black;
 
−
}
 
  
−
return &image.m_pixels[(y * image.m_pitch) + x * 3];
+
__global__ void blur_kernel(BGRPixel* imageIn, BGRPixel* imageOut, float* blur, int n_blur, int x, int start, int jump) {
−
}
+
int idx = blockDim.x*blockIdx.x + threadIdx.x; // Location on the row
  
−
__global__ void horizontal_blur_kernel(float* pixels, float* output, float* intergrals, int nIntegrals, int width, int height, int pitch) {
+
if (idx < x) {
−
//int p = pitch;
+
int id = start + idx;
−
//int x = width;
+
int bstart = id - (n_blur / 2)*jump;
−
//int y = height;
 
−
//int n = nIntegrals;
 
−
int idy = blockIdx.x*blockDim.x + threadIdx.x;
 
−
int idx = blockIdx.y*blockDim.y + threadIdx.y;
 
−
//int startOffset = -1 * int(nIntegrals / 2);
 
  
−
//float* dst;
+
BGRPixel pixel{ 0.0f, 0.0f, 0.0f };
−
//const float* pixel;
 
−
//const float black[3] = { 0.0f, 0.0f, 0.0f };
 
−
//float blurred_pixel[3] = { 0.0f, 0.0f, 0.0f };
 
  
−
//for (int i = 0; i < n; ++i) { // Prefetch for integrals and pixels
+
for (int i = 0; i < n_blur; ++i) {
−
// int ty = y + startOffset + i;
+
int bid = bstart + i*jump;
−
// pixel = (idx < 0 || idx >= x ||
+
float iblur = blur[i];
−
// idy < 0 || idy >= ty) ? black : &pixels[(ty * p) + idx * 3];
 
  
−
// blurred_pixel[0] += pixel[0] * intergrals[i];
+
pixel.b += imageIn[bid].b * iblur;
−
// blurred_pixel[1] += pixel[1] * intergrals[i];
+
pixel.g += imageIn[bid].g * iblur;
−
// blurred_pixel[2] += pixel[2] * intergrals[i];
+
pixel.r += imageIn[bid].r * iblur;
−
//}
+
}
  
−
//dst = &output[idy*p + idx * 3];
+
imageOut[id].b = pixel.b;
−
//dst[0] = blurred_pixel[0];
+
imageOut[id].g = pixel.g;
−
//dst[1] = blurred_pixel[1];
+
imageOut[id].r = pixel.r;
−
//dst[2] = blurred_pixel[2];
+
}
−
 
 
−
//if (idx == 0) {
 
−
output[idx*width + idy] = pixels[idx*width + idy];
 
−
 
 
−
//if (idx % 3 == 0) {
 
−
// output[idx + idy*width] = 0;
 
−
//}
 
−
//}
 
 
}
 
}
  
 
void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
 
void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
 
{
 
{
−
float* d_ipixels; // Device input pixel array 
+
int xImage = srcImage.m_width; // Width of image
−
float* d_opixels; // Device output pixel array
+
int yImage = srcImage.m_height; // Height of image
−
float* d_integrals; // Stores guassian kernel intergrals
+
int imageSize = xImage*yImage;
 +
 
 +
int xPadded = xImage + (xblursize - 1); // Width including padding
 +
int yPadded = yImage + (yblursize - 1); // Height including padding
 +
int paddedSize = xPadded*yPadded;
 +
 
 +
int xPad = xblursize / 2; // Number of padding columns on each side
 +
int yPad = yblursize / 2;
 +
int padOffset = xPadded*yPad + xPad; // Offset to first pixel in padded image
 +
 
 +
float* pinnedImage = nullptr;
 +
BGRPixel* d_padded1 = nullptr;
 +
BGRPixel* d_padded2 = nullptr;
 +
 
 +
float* d_xblur = nullptr; // XBlur integrals
 +
int n_xblur; // N
  
−
int n = srcImage.m_height*srcImage.m_pitch;
+
float* d_yblur = nullptr; // YBlur integrals
−
int nblks = (n + ntpb - 1) / ntpb;
+
int n_yblur; // N
  
−
dim3 dimBlock(1, 3);
+
// Allocate memory for host and device
−
dim3 dimGrid(srcImage.m_width*3, srcImage.m_height);
+
check(cudaHostAlloc((void**)&pinnedImage, 3 * imageSize * sizeof(float), 0));
 +
check(cudaMalloc((void**)&d_padded1, paddedSize * sizeof(BGRPixel)));
 +
check(cudaMalloc((void**)&d_padded2, paddedSize * sizeof(BGRPixel)));
  
−
check(cudaMalloc((void**)&d_ipixels, srcImage.m_pitch*srcImage.m_height * sizeof(float)));
+
// Copy image to pinned memory
−
check(cudaMalloc((void**)&d_opixels, srcImage.m_pitch*srcImage.m_height*sizeof(float)));
+
for (int i = 0; i < 3 * imageSize; ++i) {
 +
pinnedImage[i] = (float)srcImage.m_pixels[i];
 +
}
  
 +
// Allocate and assign intergrals
 
{
 
{
−
std::vector<float> temp(srcImage.m_pixels.size());
+
auto row_blur = GaussianKernelIntegrals(xblursigma, xblursize);
−
std::transform(srcImage.m_pixels.begin(), srcImage.m_pixels.end(), temp.begin(), [](auto e) {
+
auto col_blur = GaussianKernelIntegrals(yblursigma, yblursize);
−
return e / 255.0f;
+
 
−
});
+
// ROW
 +
n_xblur = row_blur.size();
 +
check(cudaMalloc((void**)&d_xblur, n_xblur * sizeof(float)));
 +
check(cudaMemcpy(d_xblur, row_blur.data(), n_xblur * sizeof(float), cudaMemcpyHostToDevice));
  
−
check(cudaMemcpy(d_ipixels, temp.data(), 3 * srcImage.m_width*srcImage.m_height * sizeof(float), cudaMemcpyHostToDevice));
+
// COLUMN
 +
n_yblur = col_blur.size();
 +
check(cudaMalloc((void**)&d_yblur, n_yblur * sizeof(float)));
 +
check(cudaMemcpy(d_yblur, col_blur.data(), n_yblur * sizeof(float), cudaMemcpyHostToDevice));
 
}
 
}
  
−
// horizontal blur from d_ipixels to d_opixels
 
−
{
 
−
int nIntegrals;
 
  
−
// Scoped so that the row is cleared once it's copied
+
cudaStream_t stream[STREAMS];
−
{
+
 
−
auto row = GaussianKernelIntegrals(xblursigma, xblursize);
+
int nblks = (xImage + (ntpb - 1)) / ntpb;
−
nIntegrals = row.size();
+
 
 +
for (int i = 0; i < STREAMS; ++i) {
 +
check(cudaStreamCreate(&stream[i]));
 +
}
  
−
check(cudaMalloc((void**)&d_integrals, row.size() * sizeof(float)));
+
for (int i = 0; i < yImage;) {
−
check(cudaMemcpy(d_integrals, row.data(), row.size() * sizeof(float), cudaMemcpyHostToDevice));
+
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
cudaMemcpyAsync(d_padded1 + padOffset + i*xPadded, pinnedImage + (3 * i*xImage), 3 * xImage * sizeof(float), cudaMemcpyHostToDevice, stream[j]);
 
}
 
}
 +
}
  
−
horizontal_blur_kernel <<<dimGrid, dimBlock >>> (d_ipixels, d_opixels, d_integrals, nIntegrals, srcImage.m_width, srcImage.m_height, srcImage.m_pitch);
+
for (int i = 0; i < yImage;) {
 +
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded1, d_padded2, d_xblur, n_xblur, xImage, padOffset + i*xPadded, 1);
 +
}
 +
}
  
−
cudaDeviceSynchronize();
+
for (int i = 0; i < yImage;) {
−
check(cudaGetLastError());
+
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded2, d_padded1, d_yblur, n_yblur, xImage, padOffset + i*xPadded, xPadded);
 +
}
 +
}
  
−
check(cudaFree(d_integrals));
+
for (int i = 0; i < yImage;) {
 +
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
check(cudaMemcpyAsync(pinnedImage + (3 * i*xImage), d_padded1 + padOffset + i*xPadded, xImage * sizeof(BGRPixel), cudaMemcpyDeviceToHost, stream[j]));
 +
}
 +
}
 +
 
 +
for (int i = 0; i < STREAMS; ++i) {
 +
check(cudaStreamSynchronize(stream[i]));
 +
check(cudaStreamDestroy(stream[i]));
 
}
 
}
  
 
destImage.m_width = srcImage.m_width;
 
destImage.m_width = srcImage.m_width;
 
destImage.m_height = srcImage.m_height;
 
destImage.m_height = srcImage.m_height;
−
destImage.m_pitch = srcImage.m_pitch;
+
destImage.m_pitch = srcImage.m_pitch;
−
destImage.m_pixels.resize(destImage.m_height * destImage.m_pitch);
+
destImage.m_pixels.resize(srcImage.m_pixels.size());
−
 
+
 
−
{
+
for (int i = 0; i < 3 * imageSize; i++) {
−
std::vector<float> temp(srcImage.m_pixels.size());
+
destImage.m_pixels[i] = (uint8_t)pinnedImage[i];
−
check(cudaMemcpy(temp.data(), d_opixels, 3 * srcImage.m_width*srcImage.m_height * sizeof(float), cudaMemcpyDeviceToHost));
+
};
−
std::transform(temp.begin(), temp.end(), destImage.m_pixels.begin(), [](auto e) {
+
 
−
return (int)(e * 255.0f);
+
check(cudaFree(d_xblur));
−
});
+
check(cudaFree(d_yblur));
−
}
+
 
−
 
+
check(cudaFreeHost(pinnedImage));
−
check(cudaFree(d_ipixels));
+
check(cudaFree(d_padded1));
−
check(cudaFree(d_opixels));
+
check(cudaFree(d_padded2));
−
check(cudaDeviceReset());
+
 
−
 
+
check(cudaDeviceReset());
−
 
+
}
−
//// allocate space for copying the image for destImage and tmpImage
+
 
−
//destImage.m_width = srcImage.m_width;
+
int main(int argc, char **argv)
−
//destImage.m_height = srcImage.m_height;
+
{
−
//destImage.m_pitch = srcImage.m_pitch;
+
float xblursigma, yblursigma;
−
//destImage.m_pixels.resize(destImage.m_height * destImage.m_pitch);
+
 
−
 
+
bool showUsage = argc < 5 ||
−
//SImageData tmpImage;
+
(sscanf(argv[3], "%f", &xblursigma) != 1) ||
−
//tmpImage.m_width = srcImage.m_width;
+
(sscanf(argv[4], "%f", &yblursigma) != 1);
−
//tmpImage.m_height = srcImage.m_height;
+
 
−
//tmpImage.m_pitch = srcImage.m_pitch;
+
char *srcFileName = argv[1];
−
//tmpImage.m_pixels.resize(tmpImage.m_height * tmpImage.m_pitch);
+
char *destFileName = argv[2];
−
 
+
 
−
//// horizontal blur from srcImage into tmpImage
+
if (showUsage)
−
//{
+
{
−
// auto row = GaussianKernelIntegrals(xblursigma, xblursize);
+
printf("Usage: <source> <dest> <xblur> <yblur>\nBlur values are sigma\n\n");
−
 
+
WaitForEnter();
−
// int startOffset = -1 * int(row.size() / 2);
+
return 1;
−
 
+
}
−
// for (int y = 0; y < tmpImage.m_height; ++y)
+
 
−
// {
+
// calculate pixel sizes, and make sure they are odd
−
// for (int x = 0; x < tmpImage.m_width; ++x)
+
int xblursize = PixelsNeededForSigma(xblursigma) | 1;
−
// {
+
int yblursize = PixelsNeededForSigma(yblursigma) | 1;
−
// std::array<float, 3> blurredPixel = { { 0.0f, 0.0f, 0.0f } };
+
 
−
// for (unsigned int i = 0; i < row.size(); ++i)
+
printf("Attempting to blur a 24 bit image.\n");
−
// {
+
printf("  Source=%s\n  Dest=%s\n  blur=[%0.1f, %0.1f] px=[%d,%d]\n\n", srcFileName, destFileName, xblursigma, yblursigma, xblursize, yblursize);
−
// const uint8_t *pixel = GetPixelOrBlack(srcImage, x + startOffset + i, y);
+
 
−
// blurredPixel[0] += float(pixel[0]) * row[i];
+
SImageData srcImage;
−
// blurredPixel[1] += float(pixel[1]) * row[i];
+
if (LoadImage(srcFileName, srcImage))
−
// blurredPixel[2] += float(pixel[2]) * row[i];
+
{
−
// }
+
printf("%s loaded\n", srcFileName);
−
 
+
SImageData destImage;
−
// uint8_t *destPixel = &tmpImage.m_pixels[y * tmpImage.m_pitch + x * 3];
+
 
−
 
+
auto t1 = std::chrono::high_resolution_clock::now();
−
// destPixel[0] = uint8_t(blurredPixel[0]);
+
BlurImage(srcImage, destImage, xblursigma, yblursigma, xblursize, yblursize);
−
// destPixel[1] = uint8_t(blurredPixel[1]);
+
auto t2 = std::chrono::high_resolution_clock::now();
−
// destPixel[2] = uint8_t(blurredPixel[2]);
+
 
−
// }
+
std::cout << "BlurImage time: " << std::chrono::duration_cast<std::chrono::microseconds>(t2 - t1).count() << "us" << std::endl;
−
// }
+
 
−
//}
+
 
−
 
+
if (SaveImage(destFileName, destImage))
−
//// vertical blur from tmpImage into destImage
+
printf("Blurred image saved as %s\n", destFileName);
−
//{
+
else
−
// auto row = GaussianKernelIntegrals(yblursigma, yblursize);
+
{
−
 
+
printf("Could not save blurred image as %s\n", destFileName);
−
// int startOffset = -1 * int(row.size() / 2);
+
WaitForEnter();
−
 
+
return 1;
−
// for (int y = 0; y < destImage.m_height; ++y)
+
}
−
// {
+
}
−
// for (int x = 0; x < destImage.m_width; ++x)
+
else
−
// {
+
{
−
// std::array<float, 3> blurredPixel = { { 0.0f, 0.0f, 0.0f } };
+
printf("could not read 24 bit bmp file %s\n\n", srcFileName);
−
// for (unsigned int i = 0; i < row.size(); ++i)
+
WaitForEnter();
−
// {
+
return 1;
−
// const uint8_t *pixel = GetPixelOrBlack(tmpImage, x, y + startOffset + i);
+
}
−
// blurredPixel[0] += float(pixel[0]) * row[i];
+
return 0;
−
// blurredPixel[1] += float(pixel[1]) * row[i];
+
}
−
// blurredPixel[2] += float(pixel[2]) * row[i];
+
</syntaxhighlight>
−
// }
+
 
−
 
+
|}
−
// uint8_t *destPixel = &destImage.m_pixels[y * destImage.m_pitch + x * 3];
+
 
−
 
+
== Objectives ==
−
// destPixel[0] = uint8_t(blurredPixel[0]);
+
The main objective was to not change the main function.  This objective was met, although code had to be added for profiling.
−
// destPixel[1] = uint8_t(blurredPixel[1]);
+
−
// destPixel[2] = uint8_t(blurredPixel[2]);
+
== Steps ==
−
// }
+
=== Host Memory Management ===
−
// }
+
In the original program a bmp is loaded into an vector of uint8_t.  This is not ideal for CUDA, therefore an array of pinned memory was allocated.  This array contains the same amount of elements but stores them as a structure, "BGRPixel" which is three contiguous floats.  The vector is then transferred over to pinned memory.
−
//}
+
{| class="wikitable mw-collapsible mw-collapsed"
−
}
+
! Host Memory Management - Code( ... )
 +
|-
 +
|
 +
<syntaxhighlight lang="cpp">
 +
struct SImageData
 +
{
 +
SImageData()
 +
: m_width(0)
 +
, m_height(0)
 +
{ }
 +
 
 +
long m_width;
 +
long m_height;
 +
long m_pitch;
 +
std::vector<uint8_t> m_pixels;
 +
};
 +
 
 +
struct BGRPixel {
 +
float b;
 +
float g;
 +
float r;
 +
};
 +
 
 +
 
 +
void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
 +
{
 +
int xImage = srcImage.m_width; // Width of image
 +
int yImage = srcImage.m_height; // Height of image
 +
int imageSize = xImage*yImage;
 +
 
 +
int xPadded = xImage + (xblursize - 1); // Width including padding
 +
int yPadded = yImage + (yblursize - 1); // Height including padding
 +
int paddedSize = xPadded*yPadded;
 +
 
 +
int xPad = xblursize / 2; // Number of padding columns on each side
 +
int yPad = yblursize / 2;
 +
int padOffset = xPadded*yPad + xPad; // Offset to first pixel in padded image
 +
 
 +
float* pinnedImage = nullptr;
 +
BGRPixel* d_padded1 = nullptr;
 +
BGRPixel* d_padded2 = nullptr;
 +
 
 +
        // ...
 +
 
 +
// Allocate memory for host and device
 +
check(cudaHostAlloc((void**)&pinnedImage, 3 * imageSize * sizeof(float), 0));
 +
check(cudaMalloc((void**)&d_padded1, paddedSize * sizeof(BGRPixel)));
 +
check(cudaMalloc((void**)&d_padded2, paddedSize * sizeof(BGRPixel)));
 +
 
 +
// Copy image to pinned memory
 +
for (int i = 0; i < 3 * imageSize; ++i) {
 +
pinnedImage[i] = (float)srcImage.m_pixels[i];
 +
}
 +
 
 +
        // ...
 +
}
 +
</syntaxhighlight>
 +
 
 +
|}
 +
 
 +
=== Device Memory Management ===
 +
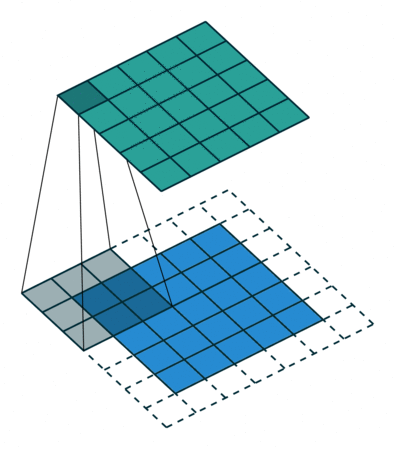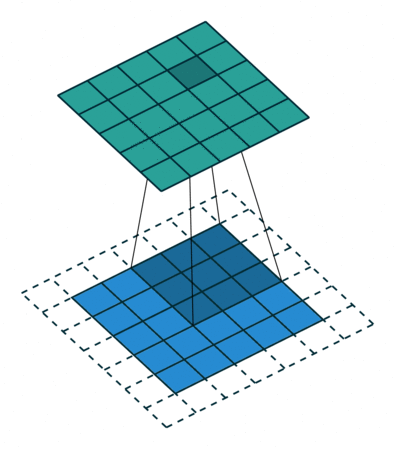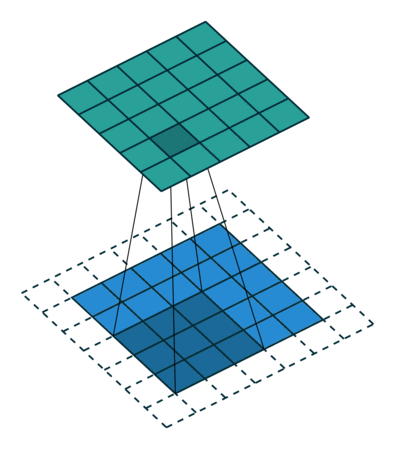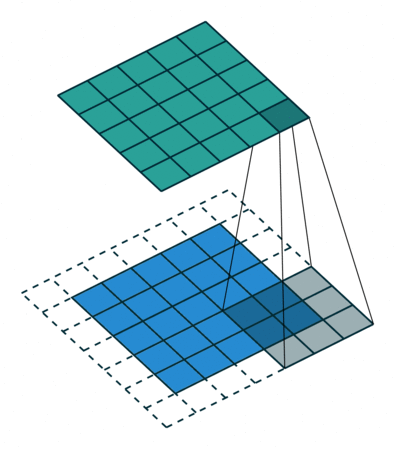
To get a blurred pixel the surrounding pixels must be sampled, in some cases this means sampling pixels outside the bounds of the image.  In the original, a simple if check was used to determine if the pixel was outside the bounds or the image, if it was a black pixel was returned instead.  This if statement most likely would have caused massive thread divergence in a kernel, therefore the images created in device memory featured additional padding of black pixels to compensate for this.  Two such images were created, one to perform horizontal blur and one to perform vertical blur.  Other small device arrays were also needed to store the Gaussian integrals that are used to produce the blurring effect.<br>
 +
{| class="wikitable mw-collapsible mw-collapsed"
 +
! Padding example
 +
|-
 +
|
 +
 
 +
<div style="display:inline;">
 +
[[File:shrunk.png]]
 +
</div>
 +
<div style="display:inline;">
 +
[[File:pad.png]]
 +
</div>
 +
<br>
 +
This is how the image would be padded for 3x3 sigma blur. 
 +
 
 +
The original image is 2560x1600 -> 11.7MB 
 +
 
 +
With blur sigmas [x = 3, y = 3] and conversion to float the padded images will be 2600x1640 -> 48.8MB 
 +
 
 +
Increase of 4.1% pixels and with the conversion for uint8_t to float total increase of 317% in memory requirements on the GPU 
 +
 
 +
Since two padded images are needed at least 97.6MB will be on the GPU
 +
 
 +
|}
 +
 
 +
=== Host to Device ===
 +
To copy the pinned image to the device an array of streams was used to asynchronously copy each row of the image over.  Doing so allowed the rows to be easily copied over while avoiding infringing on the extra padding pixels.
 +
=== Kernels ===
 +
First one image is blurred horizontally.  One image is used as a reference while the other is written to.  Kernels are also executed using the streams, so that each stream will blur a single row at a time.  After the horizontal blur is finished the vertical blur is launched in the same manner, except that the previously written to image is used as a reference while the previous reference is now written to.  The two blur are able to use the same kernel due to the fact that the pixel sampling technique works by iterating through pixels because of this the step size can be changed to sample across the row or down the column.
 +
=== Device to Host ===
 +
After that is done the image is copied back using the streams in the same way it was copied over.
 +
=== Code ===
 +
 
 +
{| class="wikitable mw-collapsible mw-collapsed"
 +
! Unoptimized* - BlurImage -- Exert( ... )
 +
|-
 +
|
 +
<syntaxhighlight lang="cpp">
 +
const int ntpb = 1024;
 +
const int STREAMS = 32;
 +
 
 +
void check(cudaError_t error) {
 +
if (error != cudaSuccess) {
 +
throw std::exception(cudaGetErrorString(error));
 +
}
 +
}
 +
 
 +
struct SImageData
 +
{
 +
SImageData()
 +
: m_width(0)
 +
, m_height(0)
 +
{ }
 +
 
 +
long m_width;
 +
long m_height;
 +
long m_pitch;
 +
std::vector<uint8_t> m_pixels;
 +
};
 +
 
 +
float Gaussian(float sigma, float x)
 +
{
 +
return expf(-(x*x) / (2.0f * sigma*sigma));
 +
}
 +
 
 +
float GaussianSimpsonIntegration(float sigma, float a, float b)
 +
{
 +
return
 +
((b - a) / 6.0f) *
 +
(Gaussian(sigma, a) + 4.0f * Gaussian(sigma, (a + b) / 2.0f) + Gaussian(sigma, b));
 +
}
 +
 
 +
std::vector<float> GaussianKernelIntegrals(float sigma, int taps)
 +
{
 +
std::vector<float> ret;
 +
float total = 0.0f;
 +
for (int i = 0; i < taps; ++i)
 +
{
 +
float x = float(i) - float(taps / 2);
 +
float value = GaussianSimpsonIntegration(sigma, x - 0.5f, x + 0.5f);
 +
ret.push_back(value);
 +
total += value;
 +
}
 +
// normalize it
 +
for (unsigned int i = 0; i < ret.size(); ++i)
 +
{
 +
ret[i] /= total;
 +
}
 +
return ret;
 +
}
 +
 
 +
struct BGRPixel {
 +
float b;
 +
float g;
 +
float r;
 +
};
 +
 
 +
__global__ void blur_kernel(BGRPixel* imageIn, BGRPixel* imageOut, float* blur, int n_blur, int x, int start, int jump) {
 +
int idx = blockDim.x*blockIdx.x + threadIdx.x; // Location on the row
 +
 
 +
if (idx < x) {
 +
int id = start + idx;
 +
int bstart = id - (n_blur / 2)*jump;
 +
 
 +
BGRPixel pixel{ 0.0f, 0.0f, 0.0f };
 +
 
 +
for (int i = 0; i < n_blur; ++i) {
 +
int bid = bstart + i*jump;
 +
float iblur = blur[i];
 +
 
 +
pixel.b += imageIn[bid].b * iblur;
 +
pixel.g += imageIn[bid].g * iblur;
 +
pixel.r += imageIn[bid].r * iblur;
 +
}
 +
 
 +
imageOut[id].b = pixel.b;
 +
imageOut[id].g = pixel.g;
 +
imageOut[id].r = pixel.r;
 +
}
 +
}
 +
 
 +
void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
 +
{
 +
int xImage = srcImage.m_width; // Width of image
 +
int yImage = srcImage.m_height; // Height of image
 +
int imageSize = xImage*yImage;
 +
 
 +
int xPadded = xImage + (xblursize - 1); // Width including padding
 +
int yPadded = yImage + (yblursize - 1); // Height including padding
 +
int paddedSize = xPadded*yPadded;
 +
 
 +
int xPad = xblursize / 2; // Number of padding columns on each side
 +
int yPad = yblursize / 2;
 +
int padOffset = xPadded*yPad + xPad; // Offset to first pixel in padded image
 +
 
 +
float* pinnedImage = nullptr;
 +
BGRPixel* d_padded1 = nullptr;
 +
BGRPixel* d_padded2 = nullptr;
 +
 
 +
float* d_xblur = nullptr; // XBlur integrals
 +
int n_xblur; // N
 +
 
 +
float* d_yblur = nullptr; // YBlur integrals
 +
int n_yblur; // N
 +
 
 +
// Allocate memory for host and device
 +
check(cudaHostAlloc((void**)&pinnedImage, 3 * imageSize * sizeof(float), 0));
 +
check(cudaMalloc((void**)&d_padded1, paddedSize * sizeof(BGRPixel)));
 +
check(cudaMalloc((void**)&d_padded2, paddedSize * sizeof(BGRPixel)));
 +
 
 +
// Copy image to pinned memory
 +
for (int i = 0; i < 3 * imageSize; ++i) {
 +
pinnedImage[i] = (float)srcImage.m_pixels[i];
 +
}
 +
 
 +
// Allocate and assign intergrals
 +
{
 +
auto row_blur = GaussianKernelIntegrals(xblursigma, xblursize);
 +
auto col_blur = GaussianKernelIntegrals(yblursigma, yblursize);
 +
 
 +
// ROW
 +
n_xblur = row_blur.size();
 +
check(cudaMalloc((void**)&d_xblur, n_xblur * sizeof(float)));
 +
check(cudaMemcpy(d_xblur, row_blur.data(), n_xblur * sizeof(float), cudaMemcpyHostToDevice));
 +
 
 +
// COLUMN
 +
n_yblur = col_blur.size();
 +
check(cudaMalloc((void**)&d_yblur, n_yblur * sizeof(float)));
 +
check(cudaMemcpy(d_yblur, col_blur.data(), n_yblur * sizeof(float), cudaMemcpyHostToDevice));
 +
}
 +
 
 +
 
 +
cudaStream_t stream[STREAMS];
 +
 
 +
int nblks = (xImage + (ntpb - 1)) / ntpb;
 +
 
 +
for (int i = 0; i < STREAMS; ++i) {
 +
check(cudaStreamCreate(&stream[i]));
 +
}
 +
 
 +
for (int i = 0; i < yImage;) {
 +
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
cudaMemcpyAsync(d_padded1 + padOffset + i*xPadded, pinnedImage + (3 * i*xImage), 3 * xImage * sizeof(float), cudaMemcpyHostToDevice, stream[j]);
 +
}
 +
}
 +
 
 +
for (int i = 0; i < yImage;) {
 +
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded1, d_padded2, d_xblur, n_xblur, xImage, padOffset + i*xPadded, 1);
 +
}
 +
}
 +
 
 +
for (int i = 0; i < yImage;) {
 +
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded2, d_padded1, d_yblur, n_yblur, xImage, padOffset + i*xPadded, xPadded);
 +
}
 +
}
 +
 
 +
for (int i = 0; i < yImage;) {
 +
for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
 +
check(cudaMemcpyAsync(pinnedImage + (3 * i*xImage), d_padded1 + padOffset + i*xPadded, xImage * sizeof(BGRPixel), cudaMemcpyDeviceToHost, stream[j]));
 +
}
 +
}
 +
 
 +
for (int i = 0; i < STREAMS; ++i) {
 +
check(cudaStreamSynchronize(stream[i]));
 +
check(cudaStreamDestroy(stream[i]));
 +
}
 +
 
 +
destImage.m_width = srcImage.m_width;
 +
destImage.m_height = srcImage.m_height;
 +
destImage.m_pitch = srcImage.m_pitch;
 +
destImage.m_pixels.resize(srcImage.m_pixels.size());
 +
 
 +
for (int i = 0; i < 3 * imageSize; i++) {
 +
destImage.m_pixels[i] = (uint8_t)pinnedImage[i];
 +
};
 +
 
 +
check(cudaFree(d_xblur));
 +
check(cudaFree(d_yblur));
 +
 
 +
check(cudaFreeHost(pinnedImage));
 +
check(cudaFree(d_padded1));
 +
check(cudaFree(d_padded2));
 +
 
 +
check(cudaDeviceReset());
 +
}
 +
 
 +
</syntaxhighlight>
 +
 
 +
|}
 +
 
 +
== Results ==
 +
Obtained using Quadro K620<br>
 +
[[File:uvso2.png]]
 +
[[File:usession.png]]
 +
[[File:ktimes.png]]
 +
<br>
 +
Using a Quadro K2000
 +
<br>
 +
[[File:streams.png]]
 +
 
 +
== Output Images ==
 +
[http://imgur.com/a/CtMOc Image Gallery]
 +
[https://seneca-my.sharepoint.com/personal/jkraitberg_myseneca_ca/_layouts/15/guestaccess.aspx?docid=099a13c42168943b587de4b59e4634e06&authkey=Afl_iMqjNyFhoYu3bopOw5E 135MB Image]
 +
[https://seneca-my.sharepoint.com/personal/jkraitberg_myseneca_ca/_layouts/15/guestaccess.aspx?docid=007880dac1dd74d09b74fc448dc3fac38&authkey=AdqHCKEjZCXzlyftjZWxFCA 135MB 3x3 Result]
 +
 
 +
== Mandelbrot ==
 +
{| class="wikitable mw-collapsible mw-collapsed"
 +
! Unoptimized - Mandelbrot( ... )
 +
|-
 +
|
 +
<syntaxhighlight lang="cpp">
 +
//C++ Includes
 +
#include <iostream>
 +
#include <complex>
 +
#include <vector>
 +
#include <chrono>
 +
#include <functional>
 +
#include <cuda_runtime.h>
 +
 
 +
//CUDA Complex Numbers
 +
#include <cuComplex.h>
 +
 
 +
//Helper Includes
 +
#include "window.h"
 +
#include "save_image.h"
 +
#include "utils.h"
 +
 
 +
const int ntpb = 32;
 +
 
 +
//Compute Color for each pixel
 +
__global__ void computeMandelbrot(  int iter_max, int* d_colors,
 +
                                    int fract_width, int fract_height,
 +
                                    int scr_width, int scr_height,
 +
                                    int fract_xmin, int fract_ymin){
 +
                                       
 +
    int row = blockIdx.y * blockDim.y + threadIdx.y;    //Row
 +
    int col = blockIdx.x * blockDim.x + threadIdx.x;    //Col
 +
 
 +
    int idx = row * scr_width + col;                    //Pixel Index
 +
 
 +
    if(col < scr_width && row < scr_height){
 +
 
 +
        //Use Floating Complex Numbers to calculate color for each pixel
 +
        int result = 0;
 +
        cuFloatComplex c = make_cuFloatComplex((float)col, (float)row);
 +
        cuFloatComplex d = make_cuFloatComplex(cuCrealf(c) / (float)scr_width * fract_width + fract_xmin , cuCimagf(c) / (float)scr_height * fract_height + fract_ymin);
 +
        cuFloatComplex z = make_cuFloatComplex(0.0f, 0.0f);
 +
 
 +
        while((cuCabsf(z) < 2.0f) && (result < iter_max)){
 +
            z = (cuCaddf(cuCmulf(z,z),d));
 +
            result++;
 +
        }
 +
        d_colors[idx] = result;                        //Output
 +
    }
 +
}
 +
 
 +
void mandelbrot(){
 +
    window<int> scr(0, 1000, 0, 1000);              //Image Size
 +
    window<float> fract(-2.2,1.2,-1.7,1.7);        //Fractal Size
 +
    int iter_max = 500;                            //Iterations
 +
    const char* fname = "mandlebrot_gpu.png";      //Output File Name
 +
    bool smooth_color = true;                      //Color Smoothing
 +
 
 +
    int nblks = (scr.width() + ntpb - 1)/ ntpb;    //Blocks
 +
    std::vector<int> colors(scr.size());            //Output Vector
 +
   
 +
    //Allocate Device Memory
 +
    int* d_colors;                                 
 +
    cudaMalloc((void**)&d_colors, scr.size() * sizeof(int));
 +
 
 +
    //Grid Layout
 +
    dim3 dGrid(nblks, nblks);
 +
    dim3 dBlock(ntpb, ntpb);
 +
 
 +
    //Execute Kernel
 +
    auto start = std::chrono::steady_clock::now();
 +
    computeMandelbrot<<<dGrid, dBlock>>>(iter_max, d_colors, fract.width(), fract.height(), scr.width(), scr.height(), fract.x_min(), fract.y_min());
 +
    cudaDeviceSynchronize();
 +
    auto end = std::chrono::steady_clock::now();
 +
 
 +
    //Output Time
 +
    std::cout << "Time to generate " << fname << " = " << std::chrono::duration <float, std::milli> (end - start).count() << " [ms]" << std::endl;
 +
 
 +
    //Copy Data back to Host
 +
    cudaMemcpy(colors.data(), d_colors, scr.size() * sizeof(int), cudaMemcpyDeviceToHost);
 +
 
 +
    //Plot Data and Free Memory
 +
    plot(scr, colors, iter_max, fname, smooth_color);
 +
    cudaFree(d_colors);
 +
}
 +
 
 +
int main(){
 +
    mandelbrot();
 +
    return 0;
 +
}
 +
</syntaxhighlight>
 +
|}
  
−
int main(int argc, char **argv)
+
=== Objectives ===
−
{
+
The main objective was refactor the get_number_iterations() function and the subsequent functions called that created the nested loops. The objective was met as all the functions were refactored into a single device function that did the calculation for a single pixel of the image. As the original program was done with doubles, all of the doubles were changed to floats.
−
float xblursigma, yblursigma;
 
  
−
bool showUsage = argc < 5 ||
+
=== Steps ===
−
(sscanf(argv[3], "%f", &xblursigma) != 1) ||
 
−
(sscanf(argv[4], "%f", &yblursigma) != 1);
 
  
−
char *srcFileName = argv[1];
+
=== Host Memory Management ===
−
char *destFileName = argv[2];
+
No changes were needed to the Host Memory as no data is copied from the host to the device. The vector on the host that contains the data was not changed and data from the device was copied to this vector to be output the plot file.
  
−
if (showUsage)
+
=== Device Memory Management ===
−
{
+
Only a single array to hold the value for each pixel was created on the device. This array has a size of image width * image height and the row and columns for each image are calculated from this which are used in the complex number calculations along with the values that specify the parameters of the fractal.
−
printf("Usage: <source> <dest> <xblur> <yblur>\nBlur values are sigma\n\n");
 
−
WaitForEnter();
 
−
return 1;
 
−
}
 
  
−
// calculate pixel sizes, and make sure they are odd
+
=== Kernels ===
−
int xblursize = PixelsNeededForSigma(xblursigma) | 1;
+
The three functions from the original code ( get_number_iterations() , escape() and scale() were refactored into a single computeMandelbrot() function. The device kernel calculates the row and column for the pixel and then uses the row and colmn values along with the picture width and fractal parameters to calculate the value. Complex floating point numbers are used using the cuComplex.h header file which also includes the operations for the complex numbers as well. As threads are not reliant on each other for any data, no use of __syncthreads() is required. As threads complete computing the values, they output the value to the d_colors array.
−
int yblursize = PixelsNeededForSigma(yblursigma) | 1;
 
  
−
printf("Attempting to blur a 24 bit image.\n");
+
=== Device to Host ===
−
printf("  Source=%s\n  Dest=%s\n  blur=[%0.1f, %0.1f] px=[%d,%d]\n\n", srcFileName, destFileName, xblursigma, yblursigma, xblursize, yblursize);
+
After that is done the image is copied back using a single memcpy to the host.
  
−
SImageData srcImage;
+
=== Results ===
−
if (LoadImage(srcFileName, srcImage))
+
The program was compiled using clang++ , icpc (Intel Parallel Studio Compiler) and NVCC for the GPU. Runtimes for the standard clang++ version were extremely slow as the size of the resultant image increased. Compiling the program using the icpc compiler brought in significant changes without modifying any code and reduced runtimes drastically for running purely on a CPU. Using the parallel version based on CUDA improved the runtime massively over the clang++ compiled version and even the icpc version as more values could be calculated in parallel.
−
{
+
[[Image:Mandelbrot.png | 750px]]
−
printf("%s loaded\n", srcFileName);
 
−
SImageData destImage;
 
−
BlurImage(srcImage, destImage, xblursigma, yblursigma, xblursize, yblursize);
 
−
if (SaveImage(destFileName, destImage))
 
−
printf("Blurred image saved as %s\n", destFileName);
 
−
else
 
−
{
 
−
printf("Could not save blurred image as %s\n", destFileName);
 
−
WaitForEnter();
 
−
return 1;
 
−
}
 
−
}
 
−
else
 
−
{
 
−
printf("could not read 24 bit bmp file %s\n\n", srcFileName);
 
−
WaitForEnter();
 
−
return 1;
 
−
}
 
−
return 0;
 
−
}
 
−
</syntaxhighlight>
 
  
−
|}
+
=== Output Images ===
 +
[http://imgur.com/a/R3ZAH Image Output]
  
−
= Assignment 3 - Optimize =
+
=== Future Optimizations ===
 +
As there isn't any data intensive tasks in this program, further optimizations would include creating streams of kernels and having them execute concurrently in order to improve runtime of the current solution.

Latest revision as of 20:30, 12 April 2017

Assignment 1 - Select and Assess

Introduction : GPU Benchmarking/Testing using Mandelbrot Sets : Kartik Nagarajan

This program generates Mandelbrot sets using CPU's and then saves them to the folder as png's using the freeimage library.

The program is open-source and can be fetched directly from GitHub from https://github.com/sol-prog/Mandelbrot_Set

To compile the program, FreeImage is required to be installed.


Compilation Instructions:

For Unix based systems: 

         g++ -std=c++11 save_image.cpp utils.cpp mandel.cpp -lfreeimage

OSX: 

         clang++ -std=c++11 save_image.cpp utils.cpp mandel.cpp -lfreeimage

The program can then be executed by running the compiled binary and it will display the time it took to generate the Mandelbrot set and save the pictures.

[Expand] Mandelbrot CPU( ... ) 
#include <iostream>
#include <complex>
#include <vector>
#include <chrono>
#include <functional>

#include "window.h"
#include "save_image.h"
#include "utils.h"

// clang++ -std=c++11 -stdlib=libc++ -O3 save_image.cpp utils.cpp mandel.cpp -lfreeimage

// Use an alias to simplify the use of complex type
using Complex = std::complex<float>;

// Convert a pixel coordinate to the complex domain
Complex scale(window<int> &scr, window<float> &fr, Complex c) {
	Complex aux(c.real() / (float)scr.width() * fr.width() + fr.x_min(),
		c.imag() / (float)scr.height() * fr.height() + fr.y_min());
	return aux;
}

// Check if a point is in the set or escapes to infinity, return the number if iterations
int escape(Complex c, int iter_max, const std::function<Complex( Complex, Complex)> &func) {
	Complex z(0);
	int iter = 0;

	while (abs(z) < 2.0 && iter < iter_max) {
		z = func(z, c);
		iter++;
	}
	return iter;
}

// Loop over each pixel from our image and check if the points associated with this pixel escape to infinity
void get_number_iterations(window<int> &scr, window<float> &fract, int iter_max, std::vector<int> &colors,
	const std::function<Complex( Complex, Complex)> &func) {
	int k = 0, progress = -1;
	for(int i = scr.y_min(); i < scr.y_max(); ++i) {
		for(int j = scr.x_min(); j < scr.x_max(); ++j) {
			Complex c((float)j, (float)i);
			c = scale(scr, fract, c);
			colors[k] = escape(c, iter_max, func);
			k++;
		}
		if(progress < (int)(i*100.0/scr.y_max())){
			progress = (int)(i*100.0/scr.y_max());
			std::cout << progress << "%\n";
		}
	}
}

void fractal(window<int> &scr, window<float> &fract, int iter_max, std::vector<int> &colors,
	const std::function<Complex( Complex, Complex)> &func, const char *fname, bool smooth_color) {
	auto start = std::chrono::steady_clock::now();
	get_number_iterations(scr, fract, iter_max, colors, func);
	auto end = std::chrono::steady_clock::now();
	std::cout << "Time to generate " << fname << " = " << std::chrono::duration <float, std::milli> (end - start).count() << " [ms]" << std::endl;

	// Save (show) the result as an image
	plot(scr, colors, iter_max, fname, smooth_color);
}

void mandelbrot() {
	// Define the size of the image
	window<int> scr(0, 1000, 0, 1000);
	// The domain in which we test for points
	window<float> fract(-2.2, 1.2, -1.7, 1.7);

	// The function used to calculate the fractal
	auto func = [] (Complex z, Complex c) -> Complex {return z * z + c; };

	int iter_max = 500;
	const char *fname = "mandelbrot.png";
	bool smooth_color = true;
	std::vector<int> colors(scr.size());

	// Experimental zoom (bugs ?). This will modify the fract window (the domain in which we calculate the fractal function) 
	//zoom(1.0, -1.225, -1.22, 0.15, 0.16, fract); //Z2
	
	fractal(scr, fract, iter_max, colors, func, fname, smooth_color);
}

void triple_mandelbrot() {
	// Define the size of the image
	window<int> scr(0, 2000, 0, 2000);
	// The domain in which we test for points
	window<float> fract(-1.5, 1.5, -1.5, 1.5);

	// The function used to calculate the fractal
	auto func = [] (Complex z, Complex c) -> Complex {return z * z * z + c; };

	int iter_max = 500;
	const char *fname = "triple_mandelbrot.png";
	bool smooth_color = true;
	std::vector<int> colors(scr.size());

	fractal(scr, fract, iter_max, colors, func, fname, smooth_color);
}

int main() {

	mandelbrot();
	// triple_mandelbrot();

	return 0;
}

Observations

The program takes a significant amount of time to run as the calculations are being done on the CPU. There are nested loops present within the program that can be parallelized to make the program faster.

The code also has the size of the image and the iterations hard-coded which can be modified to make the program significantly longer to process and make it tough on the GPU's for benchmarking and stability testing by running the process in a loop. The code is relatively straight forward and the parallelization should also be easy to implement and test.


Hotspot

Hotspot for the program was found in the fractal() function which calls the get_iterations() function that contains 2-nested for loops and a call to escape() which contains a while loop. Profiling the runtime with Instruments on OSX displayed that the fractal() function took up the most amount of runtime and this is the function that will be parallelized using CUDA. Once the function is parallelized, the iterations and size of the image can be increased in order to make the computation relatively stressful on the GPU to get a benchmark or looped in order to do stress testing for GPUs.


Profiling Data Screenshots

Profile - Profile

Hotspot Code - Hotspot Code

Introduction : GPU Benchmarking/Testing for NBody : Joshua Kraitberg

This program uses Newtonian mechanics and a four-order symplectic Candy-Rozmus integration (a symplectic algorithm guarantees exact conservation of energy and angular momentum). The initial conditions are obtained from JPL Horizons, ahd constants (like masses, gravitational constant) are those recommended by the International Astronomical Union. The program currently does not take into account effects like general relativity, the non-spherical shapes of celestial objects, tidal effects on Earth, etc. It also does not take the 500 asteroids used by JPL Horizons into accound in its model of the Solar System.

Source

Compilation Instructions:

For Unix/Linux based systems: 

   g++ -std=c++11 c++/nbody.cpp

Observations

The program is quite fast for being a single-threaded CPU application. Almost all the CPU time is spent manipulating data and iterating in vectors.

Hotspot

Essentially all the time spent running is spent in the doing calculation on vectors. The dowork function iteratively calls the CRO_step function found in integrators.h file. The CRO_step function is where most of the vector calculations take place. A large amount of is also done in the calculate_a function which is used to calulate the acceleration on all the planets.

Profiling Data and Screenshots

[Expand] NBody Hot Functions 
void dowork(double t){
	int numtimes=int(abs(t/dt));
	dt=t/double(numtimes+1);
	numtimes=numtimes+1;
	for (int i=0;i<numtimes;i++){
		CRO_step(dt,a);
	}
}  

void CRO_step(register double mydt,void (*a)()){
	long double macr_a[4] = {0.5153528374311229364, -0.085782019412973646,0.4415830236164665242, 0.1288461583653841854};
	long double macr_b[4] = {0.1344961992774310892, -0.2248198030794208058, 0.7563200005156682911, 0.3340036032863214255};
	for (int i=0;i<4;i++){
            a();
            for (int j=0;j<ncobjects;j++){
                cobjects[j]->v +=  cobjects[j]->a * mydt*macr_b[i];
                cobjects[j]->pos += cobjects[j]->v  * mydt*macr_a[i]; 
			}
	} //We should really expand the loop for efficiency
}  

void calculate_a(){
	for (int j1=0;j1<ncobjects;j1++){
		cobjects[j1]->a=vect(0,0,0);
	}
	for (int j1=0; j1<ncobjects;j1++){
		for (int j2=j1+1;j2<ncobjects;j2++){
			double m1=cobjects[j1]->m;
			double m2=cobjects[j2]->m;
			vect dist=cobjects[j1]->pos-cobjects[j2]->pos;
			double magd=dist.mag();
			vect base=dist*(1.0/(magd*magd*magd));
			cobjects[j1]->a+=base*(-m2);
			cobjects[j2]->a+=base*m1;
		}
	}
}
[Expand] NBody Hot Spot Data
Call graph (explanation follows)


granularity: each sample hit covers 4 byte(s) for 0.16% of 6.18 seconds

index % time self children called name 

                                                <spontaneous>

[1] 99.7 0.00 6.16 main [1] 

               0.00    6.15       1/1           dowork(double) [3]
               0.00    0.01       1/1           totalL() [14]
               0.00    0.00       1/1           totalE() [16]
               0.00    0.00       1/1           initialize() [17]
               0.00    0.00      28/32712799     vect::operator-(vect const&) [8]
               0.00    0.00      14/118268959     vect::operator*(double const&) [5]
               0.00    0.00      14/5032775     vect::operator=(vect const&) [11]
               0.00    0.00      42/42          std::vector<int, std::allocator<int> >::operator[](unsigned int) [22]
               0.00    0.00      16/16          bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*) [33]
               0.00    0.00      15/35          std::vector<int, std::allocator<int> >::size() const [23]
               0.00    0.00      14/14          std::vector<int, std::allocator<int> >::push_back(int const&) [39]
               0.00    0.00      14/14          getobj(int) [36]
               0.00    0.00       3/3           std::vector<double, std::allocator<double> >::operator[](unsigned int) [90]
               0.00    0.00       2/2           print_hline() [94]
               0.00    0.00       2/10          std::vector<double, std::allocator<double> >::size() const [45]
               0.00    0.00       1/1           std::ios_base::precision(int) [146]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::vector() [142]
               0.00    0.00       1/1           std::vector<int, std::allocator<int> >::vector() [144]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::push_back(double const&) [141]
               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::vector() [135]
               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::~vector() [136]
               0.00    0.00       1/1           JD(tm*) [103]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::push_back(double&&) [140]
               0.00    0.00       1/1           std::vector<int, std::allocator<int> >::~vector() [145]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::~vector() [143]

               0.14    6.01   89870/89870       dowork(double) [3]

[2] 99.6 0.14 6.01 89870 CRO_step(double, void (*)()) [2] 

               1.18    4.22  359480/359480      calculate_a() [4]
               0.20    0.29 20130880/118268959     vect::operator*(double const&) [5]
               0.12    0.00 10065440/75490814     vect::operator+=(vect const&) [7]

               0.00    6.15       1/1           main [1]

[3] 99.6 0.00 6.15 1 dowork(double) [3] 

               0.14    6.01   89870/89870       CRO_step(double, void (*)()) [2]
               0.00    0.00       1/1           std::abs(double) [147]

               1.18    4.22  359480/359480      CRO_step(double, void (*)()) [2]

[4] 87.5 1.18 4.22 359480 calculate_a() [4] 

               1.00    1.39 98138040/118268959     vect::operator*(double const&) [5]
               0.78    0.00 65425360/75490814     vect::operator+=(vect const&) [7]
               0.26    0.37 32712680/32712799     vect::operator-(vect const&) [8]
               0.32    0.00 32712680/32712785     vect::mag() [10]
               0.08    0.00 5032720/5032775     vect::operator=(vect const&) [11]
               0.01    0.00 5032720/5032775     vect::vect(double, double, double) [13]

               0.00    0.00      11/118268959     initialize() [17]
               0.00    0.00      14/118268959     main [1]
               0.00    0.00      14/118268959     totalL() [14]
               0.20    0.29 20130880/118268959     CRO_step(double, void (*)()) [2]
               1.00    1.39 98138040/118268959     calculate_a() [4]

[5] 46.5 1.20 1.67 118268959 vect::operator*(double const&) [5] 

               1.67    0.00 118268959/118268959     vect::operator*=(double const&) [6]

               1.67    0.00 118268959/118268959     vect::operator*(double const&) [5]

[6] 27.1 1.67 0.00 118268959 vect::operator*=(double const&) [6] 

               0.00    0.00      14/75490814     totalL() [14]
               0.12    0.00 10065440/75490814     CRO_step(double, void (*)()) [2]
               0.78    0.00 65425360/75490814     calculate_a() [4]

[7] 14.6 0.91 0.00 75490814 vect::operator+=(vect const&) [7] 

               0.00    0.00      28/32712799     main [1]
               0.00    0.00      91/32712799     totalE() [16]
               0.26    0.37 32712680/32712799     calculate_a() [4]

[8] 10.4 0.27 0.38 32712799 vect::operator-(vect const&) [8] 

               0.38    0.00 32712799/32712799     vect::operator-=(vect const&) [9]

               0.38    0.00 32712799/32712799     vect::operator-(vect const&) [8]

[9] 6.1 0.38 0.00 32712799 vect::operator-=(vect const&) [9] 

               0.00    0.00     105/32712785     totalE() [16]
               0.32    0.00 32712680/32712785     calculate_a() [4]

[10] 5.2 0.32 0.00 32712785 vect::mag() [10] 

               0.00    0.00      14/5032775     main [1]
               0.00    0.00      41/5032775     initialize() [17]
               0.08    0.00 5032720/5032775     calculate_a() [4]

[11] 1.4 0.08 0.00 5032775 vect::operator=(vect const&) [11] 

                                                <spontaneous>

[12] 0.3 0.02 0.00 vect::operator+(vect const&) [12] 

               0.00    0.00      14/5032775     cross(vect const&, vect const&) [15]
               0.00    0.00      41/5032775     initialize() [17]
               0.01    0.00 5032720/5032775     calculate_a() [4]

[13] 0.2 0.01 0.00 5032775 vect::vect(double, double, double) [13] 

               0.00    0.01       1/1           main [1]

[14] 0.1 0.00 0.01 1 totalL() [14] 

               0.01    0.00      14/14          cross(vect const&, vect const&) [15]
               0.00    0.00      14/118268959     vect::operator*(double const&) [5]
               0.00    0.00      14/75490814     vect::operator+=(vect const&) [7]
               0.00    0.00       1/85          vect::vect() [21]

               0.01    0.00      14/14          totalL() [14]

[15] 0.1 0.01 0.00 14 cross(vect const&, vect const&) [15] 

               0.00    0.00      14/5032775     vect::vect(double, double, double) [13]
[Expand] NBody gprof Complete Data (Warning: long)
Call graph (explanation follows)


granularity: each sample hit covers 4 byte(s) for 0.16% of 6.18 seconds

index % time self children called name 

                                                <spontaneous>

[1] 99.7 0.00 6.16 main [1] 

               0.00    6.15       1/1           dowork(double) [3]
               0.00    0.01       1/1           totalL() [14]
               0.00    0.00       1/1           totalE() [16]
               0.00    0.00       1/1           initialize() [17]
               0.00    0.00      28/32712799     vect::operator-(vect const&) [8]
               0.00    0.00      14/118268959     vect::operator*(double const&) [5]
               0.00    0.00      14/5032775     vect::operator=(vect const&) [11]
               0.00    0.00      42/42          std::vector<int, std::allocator<int> >::operator[](unsigned int) [22]
               0.00    0.00      16/16          bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*) [33]
               0.00    0.00      15/35          std::vector<int, std::allocator<int> >::size() const [23]
               0.00    0.00      14/14          std::vector<int, std::allocator<int> >::push_back(int const&) [39]
               0.00    0.00      14/14          getobj(int) [36]
               0.00    0.00       3/3           std::vector<double, std::allocator<double> >::operator[](unsigned int) [90]
               0.00    0.00       2/2           print_hline() [94]
               0.00    0.00       2/10          std::vector<double, std::allocator<double> >::size() const [45]
               0.00    0.00       1/1           std::ios_base::precision(int) [146]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::vector() [142]
               0.00    0.00       1/1           std::vector<int, std::allocator<int> >::vector() [144]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::push_back(double const&) [141]
               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::vector() [135]
               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::~vector() [136]
               0.00    0.00       1/1           JD(tm*) [103]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::push_back(double&&) [140]
               0.00    0.00       1/1           std::vector<int, std::allocator<int> >::~vector() [145]
               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::~vector() [143]

               0.14    6.01   89870/89870       dowork(double) [3]

[2] 99.6 0.14 6.01 89870 CRO_step(double, void (*)()) [2] 

               1.18    4.22  359480/359480      calculate_a() [4]
               0.20    0.29 20130880/118268959     vect::operator*(double const&) [5]
               0.12    0.00 10065440/75490814     vect::operator+=(vect const&) [7]

               0.00    6.15       1/1           main [1]

[3] 99.6 0.00 6.15 1 dowork(double) [3] 

               0.14    6.01   89870/89870       CRO_step(double, void (*)()) [2]
               0.00    0.00       1/1           std::abs(double) [147]

               1.18    4.22  359480/359480      CRO_step(double, void (*)()) [2]

[4] 87.5 1.18 4.22 359480 calculate_a() [4] 

               1.00    1.39 98138040/118268959     vect::operator*(double const&) [5]
               0.78    0.00 65425360/75490814     vect::operator+=(vect const&) [7]
               0.26    0.37 32712680/32712799     vect::operator-(vect const&) [8]
               0.32    0.00 32712680/32712785     vect::mag() [10]
               0.08    0.00 5032720/5032775     vect::operator=(vect const&) [11]
               0.01    0.00 5032720/5032775     vect::vect(double, double, double) [13]

               0.00    0.00      11/118268959     initialize() [17]
               0.00    0.00      14/118268959     main [1]
               0.00    0.00      14/118268959     totalL() [14]
               0.20    0.29 20130880/118268959     CRO_step(double, void (*)()) [2]
               1.00    1.39 98138040/118268959     calculate_a() [4]

[5] 46.5 1.20 1.67 118268959 vect::operator*(double const&) [5] 

               1.67    0.00 118268959/118268959     vect::operator*=(double const&) [6]

               1.67    0.00 118268959/118268959     vect::operator*(double const&) [5]

[6] 27.1 1.67 0.00 118268959 vect::operator*=(double const&) [6] 

               0.00    0.00      14/75490814     totalL() [14]
               0.12    0.00 10065440/75490814     CRO_step(double, void (*)()) [2]
               0.78    0.00 65425360/75490814     calculate_a() [4]

[7] 14.6 0.91 0.00 75490814 vect::operator+=(vect const&) [7] 

               0.00    0.00      28/32712799     main [1]
               0.00    0.00      91/32712799     totalE() [16]
               0.26    0.37 32712680/32712799     calculate_a() [4]

[8] 10.4 0.27 0.38 32712799 vect::operator-(vect const&) [8] 

               0.38    0.00 32712799/32712799     vect::operator-=(vect const&) [9]

               0.38    0.00 32712799/32712799     vect::operator-(vect const&) [8]

[9] 6.1 0.38 0.00 32712799 vect::operator-=(vect const&) [9] 

               0.00    0.00     105/32712785     totalE() [16]
               0.32    0.00 32712680/32712785     calculate_a() [4]

[10] 5.2 0.32 0.00 32712785 vect::mag() [10] 

               0.00    0.00      14/5032775     main [1]
               0.00    0.00      41/5032775     initialize() [17]
               0.08    0.00 5032720/5032775     calculate_a() [4]

[11] 1.4 0.08 0.00 5032775 vect::operator=(vect const&) [11] 

                                                <spontaneous>

[12] 0.3 0.02 0.00 vect::operator+(vect const&) [12] 

               0.00    0.00      14/5032775     cross(vect const&, vect const&) [15]
               0.00    0.00      41/5032775     initialize() [17]
               0.01    0.00 5032720/5032775     calculate_a() [4]

[13] 0.2 0.01 0.00 5032775 vect::vect(double, double, double) [13] 

               0.00    0.01       1/1           main [1]

[14] 0.1 0.00 0.01 1 totalL() [14] 

               0.01    0.00      14/14          cross(vect const&, vect const&) [15]
               0.00    0.00      14/118268959     vect::operator*(double const&) [5]
               0.00    0.00      14/75490814     vect::operator+=(vect const&) [7]
               0.00    0.00       1/85          vect::vect() [21]

               0.01    0.00      14/14          totalL() [14]

[15] 0.1 0.01 0.00 14 cross(vect const&, vect const&) [15] 

               0.00    0.00      14/5032775     vect::vect(double, double, double) [13]

               0.00    0.00       1/1           main [1]

[16] 0.0 0.00 0.00 1 totalE() [16] 

               0.00    0.00      91/32712799     vect::operator-(vect const&) [8]
               0.00    0.00     105/32712785     vect::mag() [10]
               0.00    0.00      14/14          __gnu_cxx::__promote_2<__gnu_cxx::__enable_if<(std::__is_arithmetic<double>::__value)&&(std::__is_arithmetic<int>::__value), double>::__type, int>::__type std::pow<double, int>(double, int) [40]

               0.00    0.00       1/1           main [1]

[17] 0.0 0.00 0.00 1 initialize() [17] 

               0.00    0.00      41/5032775     vect::operator=(vect const&) [11]
               0.00    0.00      11/118268959     vect::operator*(double const&) [5]
               0.00    0.00      41/5032775     vect::vect(double, double, double) [13]

               0.00    0.00       1/85          totalL() [14]
               0.00    0.00      84/85          cobject::cobject() [37]

[21] 0.0 0.00 0.00 85 vect::vect() [21] 

               0.00    0.00      42/42          main [1]

[22] 0.0 0.00 0.00 42 std::vector<int, std::allocator<int> >::operator[](unsigned int) [22] 

               0.00    0.00      15/35          main [1]
               0.00    0.00      20/35          std::vector<int, std::allocator<int> >::_M_check_len(unsigned int, char const*) const [71]

[23] 0.0 0.00 0.00 35 std::vector<int, std::allocator<int> >::size() const [23] 

               0.00    0.00      30/30          std::_Niter_base<int*>::iterator_type std::__niter_base<int*>(int*) [25]

[24] 0.0 0.00 0.00 30 std::_Iter_base<int*, false>::_S_base(int*) [24] 

               0.00    0.00      30/30          int* std::__copy_move_a2<true, int*, int*>(int*, int*, int*) [50]

[25] 0.0 0.00 0.00 30 std::_Niter_base<int*>::iterator_type std::__niter_base<int*>(int*) [25] 

               0.00    0.00      30/30          std::_Iter_base<int*, false>::_S_base(int*) [24]

               0.00    0.00      10/20          void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]
               0.00    0.00      10/20          __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::difference_type __gnu_cxx::operator-<int*, std::vector<int, std::allocator<int> > >(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&, __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&) [70]

[26] 0.0 0.00 0.00 20 __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::base() const [26] 

               0.00    0.00      20/20          std::_Iter_base<std::move_iterator<int*>, true>::_S_base(std::move_iterator<int*>) [28]

[27] 0.0 0.00 0.00 20 std::move_iterator<int*>::base() const [27] 

               0.00    0.00      20/20          std::_Miter_base<std::move_iterator<int*> >::iterator_type std::__miter_base<std::move_iterator<int*> >(std::move_iterator<int*>) [30]

[28] 0.0 0.00 0.00 20 std::_Iter_base<std::move_iterator<int*>, true>::_S_base(std::move_iterator<int*>) [28] 

               0.00    0.00      20/20          std::move_iterator<int*>::base() const [27]

               0.00    0.00      20/20          std::move_iterator<int*> std::make_move_iterator<int*>(int* const&) [31]

[29] 0.0 0.00 0.00 20 std::move_iterator<int*>::move_iterator(int*) [29] 

               0.00    0.00      20/20          int* std::copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [54]

[30] 0.0 0.00 0.00 20 std::_Miter_base<std::move_iterator<int*> >::iterator_type std::__miter_base<std::move_iterator<int*> >(std::move_iterator<int*>) [30] 

               0.00    0.00      20/20          std::_Iter_base<std::move_iterator<int*>, true>::_S_base(std::move_iterator<int*>) [28]

               0.00    0.00      20/20          int* std::__uninitialized_move_a<int*, int*, std::allocator<int> >(int*, int*, int*, std::allocator<int>&) [53]

[31] 0.0 0.00 0.00 20 std::move_iterator<int*> std::make_move_iterator<int*>(int* const&) [31] 

               0.00    0.00      20/20          std::move_iterator<int*>::move_iterator(int*) [29]

               0.00    0.00       1/16          std::vector<int, std::allocator<int> >::~vector() [145]
               0.00    0.00      15/16          void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[32] 0.0 0.00 0.00 16 std::_Vector_base<int, std::allocator<int> >::_M_get_Tp_allocator() [32] 

               0.00    0.00      16/16          main [1]

[33] 0.0 0.00 0.00 16 bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*) [33] 

               0.00    0.00       1/16          __gnu_cxx::new_allocator<double>::construct(double*, double const&) [108]
               0.00    0.00       1/16          void __gnu_cxx::new_allocator<double>::construct<double>(double*, double&&) [109]
               0.00    0.00      14/16          __gnu_cxx::new_allocator<int>::construct(int*, int const&) [38]

[34] 0.0 0.00 0.00 16 operator new(unsigned int, void*) [34] 

               0.00    0.00       5/15          __gnu_cxx::new_allocator<int>::allocate(unsigned int, void const*) [69]
               0.00    0.00      10/15          std::vector<int, std::allocator<int> >::max_size() const [46]

[35] 0.0 0.00 0.00 15 __gnu_cxx::new_allocator<int>::max_size() const [35] 

               0.00    0.00      14/14          main [1]

[36] 0.0 0.00 0.00 14 getobj(int) [36] 

               0.00    0.00      14/14          __static_initialization_and_destruction_0(int, int) [105]

[37] 0.0 0.00 0.00 14 cobject::cobject() [37] 

               0.00    0.00      84/85          vect::vect() [21]

               0.00    0.00       5/14          void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]
               0.00    0.00       9/14          std::vector<int, std::allocator<int> >::push_back(int const&) [39]

[38] 0.0 0.00 0.00 14 __gnu_cxx::new_allocator<int>::construct(int*, int const&) [38] 

               0.00    0.00      14/16          operator new(unsigned int, void*) [34]

               0.00    0.00      14/14          main [1]

[39] 0.0 0.00 0.00 14 std::vector<int, std::allocator<int> >::push_back(int const&) [39] 

               0.00    0.00       9/14          __gnu_cxx::new_allocator<int>::construct(int*, int const&) [38]
               0.00    0.00       5/5           std::vector<int, std::allocator<int> >::end() [74]
               0.00    0.00       5/5           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

               0.00    0.00      14/14          totalE() [16]

[40] 0.0 0.00 0.00 14 __gnu_cxx::__promote_2<__gnu_cxx::__enable_if<(std::__is_arithmetic<double>::__value)&&(std::__is_arithmetic<int>::__value), double>::__type, int>::__type std::pow<double, int>(double, int) [40] 

               0.00    0.00      12/12          std::_Niter_base<double*>::iterator_type std::__niter_base<double*>(double*) [42]

[41] 0.0 0.00 0.00 12 std::_Iter_base<double*, false>::_S_base(double*) [41] 

               0.00    0.00      12/12          double* std::__copy_move_a2<true, double*, double*>(double*, double*, double*) [83]

[42] 0.0 0.00 0.00 12 std::_Niter_base<double*>::iterator_type std::__niter_base<double*>(double*) [42] 

               0.00    0.00      12/12          std::_Iter_base<double*, false>::_S_base(double*) [41]

               0.00    0.00       5/10          std::vector<int, std::allocator<int> >::end() [74]
               0.00    0.00       5/10          std::vector<int, std::allocator<int> >::begin() [75]

[43] 0.0 0.00 0.00 10 __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::__normal_iterator(int* const&) [43] 

               0.00    0.00      10/10          std::vector<int, std::allocator<int> >::max_size() const [46]

[44] 0.0 0.00 0.00 10 std::_Vector_base<int, std::allocator<int> >::_M_get_Tp_allocator() const [44] 

               0.00    0.00       2/10          main [1]
               0.00    0.00       8/10          std::vector<double, std::allocator<double> >::_M_check_len(unsigned int, char const*) const [98]

[45] 0.0 0.00 0.00 10 std::vector<double, std::allocator<double> >::size() const [45] 

               0.00    0.00      10/10          std::vector<int, std::allocator<int> >::_M_check_len(unsigned int, char const*) const [71]

[46] 0.0 0.00 0.00 10 std::vector<int, std::allocator<int> >::max_size() const [46] 

               0.00    0.00      10/10          std::_Vector_base<int, std::allocator<int> >::_M_get_Tp_allocator() const [44]
               0.00    0.00      10/15          __gnu_cxx::new_allocator<int>::max_size() const [35]

               0.00    0.00      10/10          int* std::__copy_move_a<true, int*, int*>(int*, int*, int*) [49]

[47] 0.0 0.00 0.00 10 int* std::__copy_move<true, true, std::random_access_iterator_tag>::__copy_m<int>(int const*, int const*, int*) [47] 

               0.00    0.00      10/10          int* std::uninitialized_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [51]

[48] 0.0 0.00 0.00 10 int* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [48] 

               0.00    0.00      10/10          int* std::copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [54]

               0.00    0.00      10/10          int* std::__copy_move_a2<true, int*, int*>(int*, int*, int*) [50]

[49] 0.0 0.00 0.00 10 int* std::__copy_move_a<true, int*, int*>(int*, int*, int*) [49] 

               0.00    0.00      10/10          int* std::__copy_move<true, true, std::random_access_iterator_tag>::__copy_m<int>(int const*, int const*, int*) [47]

               0.00    0.00      10/10          int* std::copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [54]

[50] 0.0 0.00 0.00 10 int* std::__copy_move_a2<true, int*, int*>(int*, int*, int*) [50] 

               0.00    0.00      30/30          std::_Niter_base<int*>::iterator_type std::__niter_base<int*>(int*) [25]
               0.00    0.00      10/10          int* std::__copy_move_a<true, int*, int*>(int*, int*, int*) [49]

               0.00    0.00      10/10          int* std::__uninitialized_copy_a<std::move_iterator<int*>, int*, int>(std::move_iterator<int*>, std::move_iterator<int*>, int*, std::allocator<int>&) [52]

[51] 0.0 0.00 0.00 10 int* std::uninitialized_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [51] 

               0.00    0.00      10/10          int* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [48]

               0.00    0.00      10/10          int* std::__uninitialized_move_a<int*, int*, std::allocator<int> >(int*, int*, int*, std::allocator<int>&) [53]

[52] 0.0 0.00 0.00 10 int* std::__uninitialized_copy_a<std::move_iterator<int*>, int*, int>(std::move_iterator<int*>, std::move_iterator<int*>, int*, std::allocator<int>&) [52] 

               0.00    0.00      10/10          int* std::uninitialized_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [51]

               0.00    0.00      10/10          void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[53] 0.0 0.00 0.00 10 int* std::__uninitialized_move_a<int*, int*, std::allocator<int> >(int*, int*, int*, std::allocator<int>&) [53] 

               0.00    0.00      20/20          std::move_iterator<int*> std::make_move_iterator<int*>(int* const&) [31]
               0.00    0.00      10/10          int* std::__uninitialized_copy_a<std::move_iterator<int*>, int*, int>(std::move_iterator<int*>, std::move_iterator<int*>, int*, std::allocator<int>&) [52]

               0.00    0.00      10/10          int* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [48]

[54] 0.0 0.00 0.00 10 int* std::copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [54] 

               0.00    0.00      20/20          std::_Miter_base<std::move_iterator<int*> >::iterator_type std::__miter_base<std::move_iterator<int*> >(std::move_iterator<int*>) [30]
               0.00    0.00      10/10          int* std::__copy_move_a2<true, int*, int*>(int*, int*, int*) [50]

               0.00    0.00       2/8           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       2/8           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]
               0.00    0.00       4/8           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::difference_type __gnu_cxx::operator-<double*, std::vector<double, std::allocator<double> > >(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&, __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&) [97]

[55] 0.0 0.00 0.00 8 __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::base() const [55] 

               0.00    0.00       8/8           std::_Iter_base<std::move_iterator<double*>, true>::_S_base(std::move_iterator<double*>) [57]

[56] 0.0 0.00 0.00 8 std::move_iterator<double*>::base() const [56] 

               0.00    0.00       8/8           std::_Miter_base<std::move_iterator<double*> >::iterator_type std::__miter_base<std::move_iterator<double*> >(std::move_iterator<double*>) [59]

[57] 0.0 0.00 0.00 8 std::_Iter_base<std::move_iterator<double*>, true>::_S_base(std::move_iterator<double*>) [57] 

               0.00    0.00       8/8           std::move_iterator<double*>::base() const [56]

               0.00    0.00       8/8           std::move_iterator<double*> std::make_move_iterator<double*>(double* const&) [60]

[58] 0.0 0.00 0.00 8 std::move_iterator<double*>::move_iterator(double*) [58] 

               0.00    0.00       8/8           double* std::copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [87]

[59] 0.0 0.00 0.00 8 std::_Miter_base<std::move_iterator<double*> >::iterator_type std::__miter_base<std::move_iterator<double*> >(std::move_iterator<double*>) [59] 

               0.00    0.00       8/8           std::_Iter_base<std::move_iterator<double*>, true>::_S_base(std::move_iterator<double*>) [57]

               0.00    0.00       8/8           double* std::__uninitialized_move_a<double*, double*, std::allocator<double> >(double*, double*, double*, std::allocator<double>&) [86]

[60] 0.0 0.00 0.00 8 std::move_iterator<double*> std::make_move_iterator<double*>(double* const&) [60] 

               0.00    0.00       8/8           std::move_iterator<double*>::move_iterator(double*) [58]

               0.00    0.00       1/7           std::vector<double, std::allocator<double> >::~vector() [143]
               0.00    0.00       3/7           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       3/7           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[61] 0.0 0.00 0.00 7 std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() [61] 

               0.00    0.00       2/7           std::vector<double, std::allocator<double> >::_M_check_len(unsigned int, char const*) const [98]
               0.00    0.00       5/7           std::vector<int, std::allocator<int> >::_M_check_len(unsigned int, char const*) const [71]

[62] 0.0 0.00 0.00 7 unsigned int const& std::max<unsigned int>(unsigned int const&, unsigned int const&) [62] 

               0.00    0.00       2/6           __gnu_cxx::new_allocator<double>::allocate(unsigned int, void const*) [96]
               0.00    0.00       4/6           std::vector<double, std::allocator<double> >::max_size() const [79]

[63] 0.0 0.00 0.00 6 __gnu_cxx::new_allocator<double>::max_size() const [63] 

               0.00    0.00       6/6           void std::_Destroy<int*>(int*, int*) [66]

[64] 0.0 0.00 0.00 6 void std::_Destroy_aux<true>::__destroy<int*>(int*, int*) [64] 

               0.00    0.00       1/6           std::_Vector_base<int, std::allocator<int> >::~_Vector_base() [134]
               0.00    0.00       5/6           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[65] 0.0 0.00 0.00 6 std::_Vector_base<int, std::allocator<int> >::_M_deallocate(int*, unsigned int) [65] 

               0.00    0.00       5/5           __gnu_cxx::new_allocator<int>::deallocate(int*, unsigned int) [68]

               0.00    0.00       6/6           void std::_Destroy<int*, int>(int*, int*, std::allocator<int>&) [67]

[66] 0.0 0.00 0.00 6 void std::_Destroy<int*>(int*, int*) [66] 

               0.00    0.00       6/6           void std::_Destroy_aux<true>::__destroy<int*>(int*, int*) [64]

               0.00    0.00       1/6           std::vector<int, std::allocator<int> >::~vector() [145]
               0.00    0.00       5/6           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[67] 0.0 0.00 0.00 6 void std::_Destroy<int*, int>(int*, int*, std::allocator<int>&) [67] 

               0.00    0.00       6/6           void std::_Destroy<int*>(int*, int*) [66]

               0.00    0.00       5/5           std::_Vector_base<int, std::allocator<int> >::_M_deallocate(int*, unsigned int) [65]

[68] 0.0 0.00 0.00 5 __gnu_cxx::new_allocator<int>::deallocate(int*, unsigned int) [68] 

               0.00    0.00       5/5           std::_Vector_base<int, std::allocator<int> >::_M_allocate(unsigned int) [72]

[69] 0.0 0.00 0.00 5 __gnu_cxx::new_allocator<int>::allocate(unsigned int, void const*) [69] 

               0.00    0.00       5/15          __gnu_cxx::new_allocator<int>::max_size() const [35]

               0.00    0.00       5/5           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[70] 0.0 0.00 0.00 5 __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::difference_type __gnu_cxx::operator-<int*, std::vector<int, std::allocator<int> > >(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&, __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&) [70] 

               0.00    0.00      10/20          __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::base() const [26]

               0.00    0.00       5/5           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[71] 0.0 0.00 0.00 5 std::vector<int, std::allocator<int> >::_M_check_len(unsigned int, char const*) const [71] 

               0.00    0.00      20/35          std::vector<int, std::allocator<int> >::size() const [23]
               0.00    0.00      10/10          std::vector<int, std::allocator<int> >::max_size() const [46]
               0.00    0.00       5/7           unsigned int const& std::max<unsigned int>(unsigned int const&, unsigned int const&) [62]

               0.00    0.00       5/5           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[72] 0.0 0.00 0.00 5 std::_Vector_base<int, std::allocator<int> >::_M_allocate(unsigned int) [72] 

               0.00    0.00       5/5           __gnu_cxx::new_allocator<int>::allocate(unsigned int, void const*) [69]

               0.00    0.00       5/5           std::vector<int, std::allocator<int> >::push_back(int const&) [39]

[73] 0.0 0.00 0.00 5 void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73] 

               0.00    0.00      15/16          std::_Vector_base<int, std::allocator<int> >::_M_get_Tp_allocator() [32]
               0.00    0.00      10/20          __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::base() const [26]
               0.00    0.00      10/10          int* std::__uninitialized_move_a<int*, int*, std::allocator<int> >(int*, int*, int*, std::allocator<int>&) [53]
               0.00    0.00       5/5           std::vector<int, std::allocator<int> >::_M_check_len(unsigned int, char const*) const [71]
               0.00    0.00       5/5           std::vector<int, std::allocator<int> >::begin() [75]
               0.00    0.00       5/5           __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::difference_type __gnu_cxx::operator-<int*, std::vector<int, std::allocator<int> > >(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&, __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&) [70]
               0.00    0.00       5/5           std::_Vector_base<int, std::allocator<int> >::_M_allocate(unsigned int) [72]
               0.00    0.00       5/5           int const&&& std::forward<int const&>(std::remove_reference<int const&>::type&) [76]
               0.00    0.00       5/14          __gnu_cxx::new_allocator<int>::construct(int*, int const&) [38]
               0.00    0.00       5/6           void std::_Destroy<int*, int>(int*, int*, std::allocator<int>&) [67]
               0.00    0.00       5/6           std::_Vector_base<int, std::allocator<int> >::_M_deallocate(int*, unsigned int) [65]

               0.00    0.00       5/5           std::vector<int, std::allocator<int> >::push_back(int const&) [39]

[74] 0.0 0.00 0.00 5 std::vector<int, std::allocator<int> >::end() [74] 

               0.00    0.00       5/10          __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::__normal_iterator(int* const&) [43]

               0.00    0.00       5/5           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[75] 0.0 0.00 0.00 5 std::vector<int, std::allocator<int> >::begin() [75] 

               0.00    0.00       5/10          __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::__normal_iterator(int* const&) [43]

               0.00    0.00       5/5           void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&) [73]

[76] 0.0 0.00 0.00 5 int const&&& std::forward<int const&>(std::remove_reference<int const&>::type&) [76] 

               0.00    0.00       2/4           std::vector<double, std::allocator<double> >::end() [100]
               0.00    0.00       2/4           std::vector<double, std::allocator<double> >::begin() [101]

[77] 0.0 0.00 0.00 4 __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::__normal_iterator(double* const&) [77] 

               0.00    0.00       4/4           std::vector<double, std::allocator<double> >::max_size() const [79]

[78] 0.0 0.00 0.00 4 std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() const [78] 

               0.00    0.00       4/4           std::vector<double, std::allocator<double> >::_M_check_len(unsigned int, char const*) const [98]

[79] 0.0 0.00 0.00 4 std::vector<double, std::allocator<double> >::max_size() const [79] 

               0.00    0.00       4/4           std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() const [78]
               0.00    0.00       4/6           __gnu_cxx::new_allocator<double>::max_size() const [63]

               0.00    0.00       4/4           double* std::__copy_move_a<true, double*, double*>(double*, double*, double*) [82]

[80] 0.0 0.00 0.00 4 double* std::__copy_move<true, true, std::random_access_iterator_tag>::__copy_m<double>(double const*, double const*, double*) [80] 

               0.00    0.00       4/4           double* std::uninitialized_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [84]

[81] 0.0 0.00 0.00 4 double* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [81] 

               0.00    0.00       4/4           double* std::copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [87]

               0.00    0.00       4/4           double* std::__copy_move_a2<true, double*, double*>(double*, double*, double*) [83]

[82] 0.0 0.00 0.00 4 double* std::__copy_move_a<true, double*, double*>(double*, double*, double*) [82] 

               0.00    0.00       4/4           double* std::__copy_move<true, true, std::random_access_iterator_tag>::__copy_m<double>(double const*, double const*, double*) [80]

               0.00    0.00       4/4           double* std::copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [87]

[83] 0.0 0.00 0.00 4 double* std::__copy_move_a2<true, double*, double*>(double*, double*, double*) [83] 

               0.00    0.00      12/12          std::_Niter_base<double*>::iterator_type std::__niter_base<double*>(double*) [42]
               0.00    0.00       4/4           double* std::__copy_move_a<true, double*, double*>(double*, double*, double*) [82]

               0.00    0.00       4/4           double* std::__uninitialized_copy_a<std::move_iterator<double*>, double*, double>(std::move_iterator<double*>, std::move_iterator<double*>, double*, std::allocator<double>&) [85]

[84] 0.0 0.00 0.00 4 double* std::uninitialized_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [84] 

               0.00    0.00       4/4           double* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [81]

               0.00    0.00       4/4           double* std::__uninitialized_move_a<double*, double*, std::allocator<double> >(double*, double*, double*, std::allocator<double>&) [86]

[85] 0.0 0.00 0.00 4 double* std::__uninitialized_copy_a<std::move_iterator<double*>, double*, double>(std::move_iterator<double*>, std::move_iterator<double*>, double*, std::allocator<double>&) [85] 

               0.00    0.00       4/4           double* std::uninitialized_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [84]

               0.00    0.00       2/4           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       2/4           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[86] 0.0 0.00 0.00 4 double* std::__uninitialized_move_a<double*, double*, std::allocator<double> >(double*, double*, double*, std::allocator<double>&) [86] 

               0.00    0.00       8/8           std::move_iterator<double*> std::make_move_iterator<double*>(double* const&) [60]
               0.00    0.00       4/4           double* std::__uninitialized_copy_a<std::move_iterator<double*>, double*, double>(std::move_iterator<double*>, std::move_iterator<double*>, double*, std::allocator<double>&) [85]

               0.00    0.00       4/4           double* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [81]

[87] 0.0 0.00 0.00 4 double* std::copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [87] 

               0.00    0.00       8/8           std::_Miter_base<std::move_iterator<double*> >::iterator_type std::__miter_base<std::move_iterator<double*> >(std::move_iterator<double*>) [59]
               0.00    0.00       4/4           double* std::__copy_move_a2<true, double*, double*>(double*, double*, double*) [83]

               0.00    0.00       3/3           void std::_Destroy<double*>(double*, double*) [92]

[88] 0.0 0.00 0.00 3 void std::_Destroy_aux<true>::__destroy<double*>(double*, double*) [88] 

               0.00    0.00       1/3           std::_Vector_base<double, std::allocator<double> >::~_Vector_base() [130]
               0.00    0.00       1/3           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       1/3           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[89] 0.0 0.00 0.00 3 std::_Vector_base<double, std::allocator<double> >::_M_deallocate(double*, unsigned int) [89] 

               0.00    0.00       2/2           __gnu_cxx::new_allocator<double>::deallocate(double*, unsigned int) [95]

               0.00    0.00       3/3           main [1]

[90] 0.0 0.00 0.00 3 std::vector<double, std::allocator<double> >::operator[](unsigned int) [90] 

               0.00    0.00       1/3           void std::vector<double, std::allocator<double> >::emplace_back<double>(double&&) [137]
               0.00    0.00       1/3           void __gnu_cxx::new_allocator<double>::construct<double>(double*, double&&) [109]
               0.00    0.00       1/3           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[91] 0.0 0.00 0.00 3 double&& std::forward<double>(std::remove_reference<double>::type&) [91] 

               0.00    0.00       3/3           void std::_Destroy<double*, double>(double*, double*, std::allocator<double>&) [93]

[92] 0.0 0.00 0.00 3 void std::_Destroy<double*>(double*, double*) [92] 

               0.00    0.00       3/3           void std::_Destroy_aux<true>::__destroy<double*>(double*, double*) [88]

               0.00    0.00       1/3           std::vector<double, std::allocator<double> >::~vector() [143]
               0.00    0.00       1/3           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       1/3           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[93] 0.0 0.00 0.00 3 void std::_Destroy<double*, double>(double*, double*, std::allocator<double>&) [93] 

               0.00    0.00       3/3           void std::_Destroy<double*>(double*, double*) [92]

               0.00    0.00       2/2           main [1]

[94] 0.0 0.00 0.00 2 print_hline() [94] 

               0.00    0.00       2/2           std::_Vector_base<double, std::allocator<double> >::_M_deallocate(double*, unsigned int) [89]

[95] 0.0 0.00 0.00 2 __gnu_cxx::new_allocator<double>::deallocate(double*, unsigned int) [95] 

               0.00    0.00       2/2           std::_Vector_base<double, std::allocator<double> >::_M_allocate(unsigned int) [99]

[96] 0.0 0.00 0.00 2 __gnu_cxx::new_allocator<double>::allocate(unsigned int, void const*) [96] 

               0.00    0.00       2/6           __gnu_cxx::new_allocator<double>::max_size() const [63]

               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[97] 0.0 0.00 0.00 2 __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::difference_type __gnu_cxx::operator-<double*, std::vector<double, std::allocator<double> > >(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&, __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&) [97] 

               0.00    0.00       4/8           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::base() const [55]

               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[98] 0.0 0.00 0.00 2 std::vector<double, std::allocator<double> >::_M_check_len(unsigned int, char const*) const [98] 

               0.00    0.00       8/10          std::vector<double, std::allocator<double> >::size() const [45]
               0.00    0.00       4/4           std::vector<double, std::allocator<double> >::max_size() const [79]
               0.00    0.00       2/7           unsigned int const& std::max<unsigned int>(unsigned int const&, unsigned int const&) [62]

               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[99] 0.0 0.00 0.00 2 std::_Vector_base<double, std::allocator<double> >::_M_allocate(unsigned int) [99] 

               0.00    0.00       2/2           __gnu_cxx::new_allocator<double>::allocate(unsigned int, void const*) [96]

               0.00    0.00       1/2           std::vector<double, std::allocator<double> >::push_back(double const&) [141]
               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::emplace_back<double>(double&&) [137]

[100] 0.0 0.00 0.00 2 std::vector<double, std::allocator<double> >::end() [100] 

               0.00    0.00       2/4           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::__normal_iterator(double* const&) [77]

               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]
               0.00    0.00       1/2           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[101] 0.0 0.00 0.00 2 std::vector<double, std::allocator<double> >::begin() [101] 

               0.00    0.00       2/4           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::__normal_iterator(double* const&) [77]

               0.00    0.00       1/1           __do_global_ctors_aux [302]

[102] 0.0 0.00 0.00 1 _GLOBAL__sub_I__Z2TTd [102] 

               0.00    0.00       1/1           __static_initialization_and_destruction_0(int, int) [105]

               0.00    0.00       1/1           main [1]

[103] 0.0 0.00 0.00 1 JD(tm*) [103] 

               0.00    0.00       1/1           __static_initialization_and_destruction_0(int, int) [105]

[104] 0.0 0.00 0.00 1 TT(double) [104] 

               0.00    0.00       1/1           _GLOBAL__sub_I__Z2TTd [102]

[105] 0.0 0.00 0.00 1 __static_initialization_and_destruction_0(int, int) [105] 

               0.00    0.00      14/14          cobject::cobject() [37]
               0.00    0.00       1/1           TT(double) [104]

               0.00    0.00       1/1           std::allocator<std::string>::allocator() [114]

[106] 0.0 0.00 0.00 1 __gnu_cxx::new_allocator<std::string>::new_allocator() [106] 

               0.00    0.00       1/1           std::allocator<std::string>::~allocator() [115]

[107] 0.0 0.00 0.00 1 __gnu_cxx::new_allocator<std::string>::~new_allocator() [107] 

               0.00    0.00       1/1           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]

[108] 0.0 0.00 0.00 1 __gnu_cxx::new_allocator<double>::construct(double*, double const&) [108] 

               0.00    0.00       1/16          operator new(unsigned int, void*) [34]

               0.00    0.00       1/1           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

[109] 0.0 0.00 0.00 1 void __gnu_cxx::new_allocator<double>::construct<double>(double*, double&&) [109] 

               0.00    0.00       1/3           double&& std::forward<double>(std::remove_reference<double>::type&) [91]
               0.00    0.00       1/16          operator new(unsigned int, void*) [34]

               0.00    0.00       1/1           std::allocator<double>::allocator() [116]

[110] 0.0 0.00 0.00 1 __gnu_cxx::new_allocator<double>::new_allocator() [110] 

               0.00    0.00       1/1           std::allocator<double>::~allocator() [117]

[111] 0.0 0.00 0.00 1 __gnu_cxx::new_allocator<double>::~new_allocator() [111] 

               0.00    0.00       1/1           std::allocator<int>::allocator() [118]

[112] 0.0 0.00 0.00 1 __gnu_cxx::new_allocator<int>::new_allocator() [112] 

               0.00    0.00       1/1           std::allocator<int>::~allocator() [119]

[113] 0.0 0.00 0.00 1 __gnu_cxx::new_allocator<int>::~new_allocator() [113] 

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::_Vector_impl() [121]

[114] 0.0 0.00 0.00 1 std::allocator<std::string>::allocator() [114] 

               0.00    0.00       1/1           __gnu_cxx::new_allocator<std::string>::new_allocator() [106]

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::~_Vector_impl() [122]

[115] 0.0 0.00 0.00 1 std::allocator<std::string>::~allocator() [115] 

               0.00    0.00       1/1           __gnu_cxx::new_allocator<std::string>::~new_allocator() [107]

               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::_Vector_impl::_Vector_impl() [127]

[116] 0.0 0.00 0.00 1 std::allocator<double>::allocator() [116] 

               0.00    0.00       1/1           __gnu_cxx::new_allocator<double>::new_allocator() [110]

               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::_Vector_impl::~_Vector_impl() [128]

[117] 0.0 0.00 0.00 1 std::allocator<double>::~allocator() [117] 

               0.00    0.00       1/1           __gnu_cxx::new_allocator<double>::~new_allocator() [111]

               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::_Vector_impl::_Vector_impl() [131]

[118] 0.0 0.00 0.00 1 std::allocator<int>::allocator() [118] 

               0.00    0.00       1/1           __gnu_cxx::new_allocator<int>::new_allocator() [112]

               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::_Vector_impl::~_Vector_impl() [132]

[119] 0.0 0.00 0.00 1 std::allocator<int>::~allocator() [119] 

               0.00    0.00       1/1           __gnu_cxx::new_allocator<int>::~new_allocator() [113]

               0.00    0.00       1/1           void std::_Destroy<std::string*>(std::string*, std::string*) [150]

[120] 0.0 0.00 0.00 1 void std::_Destroy_aux<false>::__destroy<std::string*>(std::string*, std::string*) [120] 

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_base() [125]

[121] 0.0 0.00 0.00 1 std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::_Vector_impl() [121] 

               0.00    0.00       1/1           std::allocator<std::string>::allocator() [114]

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::~_Vector_base() [126]

[122] 0.0 0.00 0.00 1 std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::~_Vector_impl() [122] 

               0.00    0.00       1/1           std::allocator<std::string>::~allocator() [115]

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::~_Vector_base() [126]

[123] 0.0 0.00 0.00 1 std::_Vector_base<std::string, std::allocator<std::string> >::_M_deallocate(std::string*, unsigned int) [123] 

               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::~vector() [136]

[124] 0.0 0.00 0.00 1 std::_Vector_base<std::string, std::allocator<std::string> >::_M_get_Tp_allocator() [124] 

               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::vector() [135]

[125] 0.0 0.00 0.00 1 std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_base() [125] 

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::_Vector_impl() [121]

               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::~vector() [136]

[126] 0.0 0.00 0.00 1 std::_Vector_base<std::string, std::allocator<std::string> >::~_Vector_base() [126] 

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_M_deallocate(std::string*, unsigned int) [123]
               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::~_Vector_impl() [122]

               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::_Vector_base() [129]

[127] 0.0 0.00 0.00 1 std::_Vector_base<double, std::allocator<double> >::_Vector_impl::_Vector_impl() [127] 

               0.00    0.00       1/1           std::allocator<double>::allocator() [116]

               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::~_Vector_base() [130]

[128] 0.0 0.00 0.00 1 std::_Vector_base<double, std::allocator<double> >::_Vector_impl::~_Vector_impl() [128] 

               0.00    0.00       1/1           std::allocator<double>::~allocator() [117]

               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::vector() [142]

[129] 0.0 0.00 0.00 1 std::_Vector_base<double, std::allocator<double> >::_Vector_base() [129] 

               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::_Vector_impl::_Vector_impl() [127]

               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::~vector() [143]

[130] 0.0 0.00 0.00 1 std::_Vector_base<double, std::allocator<double> >::~_Vector_base() [130] 

               0.00    0.00       1/3           std::_Vector_base<double, std::allocator<double> >::_M_deallocate(double*, unsigned int) [89]
               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::_Vector_impl::~_Vector_impl() [128]

               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::_Vector_base() [133]

[131] 0.0 0.00 0.00 1 std::_Vector_base<int, std::allocator<int> >::_Vector_impl::_Vector_impl() [131] 

               0.00    0.00       1/1           std::allocator<int>::allocator() [118]

               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::~_Vector_base() [134]

[132] 0.0 0.00 0.00 1 std::_Vector_base<int, std::allocator<int> >::_Vector_impl::~_Vector_impl() [132] 

               0.00    0.00       1/1           std::allocator<int>::~allocator() [119]

               0.00    0.00       1/1           std::vector<int, std::allocator<int> >::vector() [144]

[133] 0.0 0.00 0.00 1 std::_Vector_base<int, std::allocator<int> >::_Vector_base() [133] 

               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::_Vector_impl::_Vector_impl() [131]

               0.00    0.00       1/1           std::vector<int, std::allocator<int> >::~vector() [145]

[134] 0.0 0.00 0.00 1 std::_Vector_base<int, std::allocator<int> >::~_Vector_base() [134] 

               0.00    0.00       1/6           std::_Vector_base<int, std::allocator<int> >::_M_deallocate(int*, unsigned int) [65]
               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::_Vector_impl::~_Vector_impl() [132]

               0.00    0.00       1/1           main [1]

[135] 0.0 0.00 0.00 1 std::vector<std::string, std::allocator<std::string> >::vector() [135] 

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_base() [125]

               0.00    0.00       1/1           main [1]

[136] 0.0 0.00 0.00 1 std::vector<std::string, std::allocator<std::string> >::~vector() [136] 

               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::_M_get_Tp_allocator() [124]
               0.00    0.00       1/1           void std::_Destroy<std::string*, std::string>(std::string*, std::string*, std::allocator<std::string>&) [151]
               0.00    0.00       1/1           std::_Vector_base<std::string, std::allocator<std::string> >::~_Vector_base() [126]

               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::push_back(double&&) [140]

[137] 0.0 0.00 0.00 1 void std::vector<double, std::allocator<double> >::emplace_back<double>(double&&) [137] 

               0.00    0.00       1/3           double&& std::forward<double>(std::remove_reference<double>::type&) [91]
               0.00    0.00       1/2           std::vector<double, std::allocator<double> >::end() [100]
               0.00    0.00       1/1           void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139]

               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::push_back(double const&) [141]

[138] 0.0 0.00 0.00 1 void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138] 

               0.00    0.00       3/7           std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() [61]
               0.00    0.00       2/8           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::base() const [55]
               0.00    0.00       2/4           double* std::__uninitialized_move_a<double*, double*, std::allocator<double> >(double*, double*, double*, std::allocator<double>&) [86]
               0.00    0.00       1/2           std::vector<double, std::allocator<double> >::_M_check_len(unsigned int, char const*) const [98]
               0.00    0.00       1/2           std::vector<double, std::allocator<double> >::begin() [101]
               0.00    0.00       1/2           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::difference_type __gnu_cxx::operator-<double*, std::vector<double, std::allocator<double> > >(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&, __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&) [97]
               0.00    0.00       1/2           std::_Vector_base<double, std::allocator<double> >::_M_allocate(unsigned int) [99]
               0.00    0.00       1/1           double const&&& std::forward<double const&>(std::remove_reference<double const&>::type&) [149]
               0.00    0.00       1/1           __gnu_cxx::new_allocator<double>::construct(double*, double const&) [108]
               0.00    0.00       1/3           void std::_Destroy<double*, double>(double*, double*, std::allocator<double>&) [93]
               0.00    0.00       1/3           std::_Vector_base<double, std::allocator<double> >::_M_deallocate(double*, unsigned int) [89]

               0.00    0.00       1/1           void std::vector<double, std::allocator<double> >::emplace_back<double>(double&&) [137]

[139] 0.0 0.00 0.00 1 void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&) [139] 

               0.00    0.00       3/7           std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() [61]
               0.00    0.00       2/8           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::base() const [55]
               0.00    0.00       2/4           double* std::__uninitialized_move_a<double*, double*, std::allocator<double> >(double*, double*, double*, std::allocator<double>&) [86]
               0.00    0.00       1/2           std::vector<double, std::allocator<double> >::_M_check_len(unsigned int, char const*) const [98]
               0.00    0.00       1/2           std::vector<double, std::allocator<double> >::begin() [101]
               0.00    0.00       1/2           __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::difference_type __gnu_cxx::operator-<double*, std::vector<double, std::allocator<double> > >(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&, __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&) [97]
               0.00    0.00       1/2           std::_Vector_base<double, std::allocator<double> >::_M_allocate(unsigned int) [99]
               0.00    0.00       1/3           double&& std::forward<double>(std::remove_reference<double>::type&) [91]
               0.00    0.00       1/1           void __gnu_cxx::new_allocator<double>::construct<double>(double*, double&&) [109]
               0.00    0.00       1/3           void std::_Destroy<double*, double>(double*, double*, std::allocator<double>&) [93]
               0.00    0.00       1/3           std::_Vector_base<double, std::allocator<double> >::_M_deallocate(double*, unsigned int) [89]

               0.00    0.00       1/1           main [1]

[140] 0.0 0.00 0.00 1 std::vector<double, std::allocator<double> >::push_back(double&&) [140] 

               0.00    0.00       1/1           std::remove_reference<double&>::type&& std::move<double&>(double&&&) [148]
               0.00    0.00       1/1           void std::vector<double, std::allocator<double> >::emplace_back<double>(double&&) [137]

               0.00    0.00       1/1           main [1]

[141] 0.0 0.00 0.00 1 std::vector<double, std::allocator<double> >::push_back(double const&) [141] 

               0.00    0.00       1/2           std::vector<double, std::allocator<double> >::end() [100]
               0.00    0.00       1/1           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]

               0.00    0.00       1/1           main [1]

[142] 0.0 0.00 0.00 1 std::vector<double, std::allocator<double> >::vector() [142] 

               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::_Vector_base() [129]

               0.00    0.00       1/1           main [1]

[143] 0.0 0.00 0.00 1 std::vector<double, std::allocator<double> >::~vector() [143] 

               0.00    0.00       1/7           std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() [61]
               0.00    0.00       1/3           void std::_Destroy<double*, double>(double*, double*, std::allocator<double>&) [93]
               0.00    0.00       1/1           std::_Vector_base<double, std::allocator<double> >::~_Vector_base() [130]

               0.00    0.00       1/1           main [1]

[144] 0.0 0.00 0.00 1 std::vector<int, std::allocator<int> >::vector() [144] 

               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::_Vector_base() [133]

               0.00    0.00       1/1           main [1]

[145] 0.0 0.00 0.00 1 std::vector<int, std::allocator<int> >::~vector() [145] 

               0.00    0.00       1/16          std::_Vector_base<int, std::allocator<int> >::_M_get_Tp_allocator() [32]
               0.00    0.00       1/6           void std::_Destroy<int*, int>(int*, int*, std::allocator<int>&) [67]
               0.00    0.00       1/1           std::_Vector_base<int, std::allocator<int> >::~_Vector_base() [134]

               0.00    0.00       1/1           main [1]

[146] 0.0 0.00 0.00 1 std::ios_base::precision(int) [146] 

               0.00    0.00       1/1           dowork(double) [3]

[147] 0.0 0.00 0.00 1 std::abs(double) [147] 

               0.00    0.00       1/1           std::vector<double, std::allocator<double> >::push_back(double&&) [140]

[148] 0.0 0.00 0.00 1 std::remove_reference<double&>::type&& std::move<double&>(double&&&) [148] 

               0.00    0.00       1/1           void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [138]

[149] 0.0 0.00 0.00 1 double const&&& std::forward<double const&>(std::remove_reference<double const&>::type&) [149] 

               0.00    0.00       1/1           void std::_Destroy<std::string*, std::string>(std::string*, std::string*, std::allocator<std::string>&) [151]

[150] 0.0 0.00 0.00 1 void std::_Destroy<std::string*>(std::string*, std::string*) [150] 

               0.00    0.00       1/1           void std::_Destroy_aux<false>::__destroy<std::string*>(std::string*, std::string*) [120]

               0.00    0.00       1/1           std::vector<std::string, std::allocator<std::string> >::~vector() [136]

[151] 0.0 0.00 0.00 1 void std::_Destroy<std::string*, std::string>(std::string*, std::string*, std::allocator<std::string>&) [151] 

               0.00    0.00       1/1           void std::_Destroy<std::string*>(std::string*, std::string*) [150]

This table describes the call tree of the program, and was sorted by
the total amount of time spent in each function and its children.

Each entry in this table consists of several lines.  The line with the
index number at the left hand margin lists the current function.
The lines above it list the functions that called this function,
and the lines below it list the functions this one called.
This line lists:
    index	A unique number given to each element of the table.

Index numbers are sorted numerically. The index number is printed next to every function name so it is easier to look up where the function in the table. 

    % time	This is the percentage of the `total' time that was spent

in this function and its children. Note that due to different viewpoints, functions excluded by options, etc, these numbers will NOT add up to 100%. 

    self	This is the total amount of time spent in this function.

    children	This is the total amount of time propagated into this

function by its children. 

    called	This is the number of times the function was called.

If the function called itself recursively, the number only includes non-recursive calls, and is followed by a `+' and the number of recursive calls. 

    name	The name of the current function.  The index number is

printed after it. If the function is a member of a cycle, the cycle number is printed between the function's name and the index number. 


For the function's parents, the fields have the following meanings:

    self	This is the amount of time that was propagated directly

from the function into this parent. 

    children	This is the amount of time that was propagated from

the function's children into this parent. 

    called	This is the number of times this parent called the

function `/' the total number of times the function was called. Recursive calls to the function are not included in the number after the `/'. 

    name	This is the name of the parent.  The parent's index

number is printed after it. If the parent is a member of a cycle, the cycle number is printed between the name and the index number. 

If the parents of the function cannot be determined, the word
`<spontaneous>' is printed in the `name' field, and all the other
fields are blank.

For the function's children, the fields have the following meanings:

    self	This is the amount of time that was propagated directly

from the child into the function. 

    children	This is the amount of time that was propagated from the

child's children to the function. 

    called	This is the number of times the function called

this child `/' the total number of times the child was called. Recursive calls by the child are not listed in the number after the `/'. 

    name	This is the name of the child.  The child's index

number is printed after it. If the child is a member of a cycle, the cycle number is printed between the name and the index number. 

If there are any cycles (circles) in the call graph, there is an
entry for the cycle-as-a-whole.  This entry shows who called the
cycle (as parents) and the members of the cycle (as children.)
The `+' recursive calls entry shows the number of function calls that
were internal to the cycle, and the calls entry for each member shows,
for that member, how many times it was called from other members of
the cycle.

� Index by function name 

[102] _GLOBAL__sub_I__Z2TTd (nbody.cpp) [98] std::vector<double, std::allocator<double> >::_M_check_len(unsigned int, char const*) const [139] void std::vector<double, std::allocator<double> >::_M_insert_aux<double>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double&&)
 [17] initialize()           [45] std::vector<double, std::allocator<double> >::size() const [100] std::vector<double, std::allocator<double> >::end()
  [4] calculate_a()          [79] std::vector<double, std::allocator<double> >::max_size() const [101] std::vector<double, std::allocator<double> >::begin()
 [94] print_hline()          [71] std::vector<int, std::allocator<int> >::_M_check_len(unsigned int, char const*) const [140] std::vector<double, std::allocator<double> >::push_back(double&&)
[103] JD(tm*)                [23] std::vector<int, std::allocator<int> >::size() const [141] std::vector<double, std::allocator<double> >::push_back(double const&)
[104] TT(double)             [46] std::vector<int, std::allocator<int> >::max_size() const [142] std::vector<double, std::allocator<double> >::vector()
[105] __static_initialization_and_destruction_0(int, int) (nbody.cpp) [114] std::allocator<std::string>::allocator() [143] std::vector<double, std::allocator<double> >::~vector()
 [15] cross(vect const&, vect const&) [115] std::allocator<std::string>::~allocator() [90] std::vector<double, std::allocator<double> >::operator[](unsigned int)
  [3] dowork(double)        [116] std::allocator<double>::allocator() [73] void std::vector<int, std::allocator<int> >::_M_insert_aux<int const&>(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >, int const&&&)
 [36] getobj(int)           [117] std::allocator<double>::~allocator() [74] std::vector<int, std::allocator<int> >::end()
 [16] totalE()              [118] std::allocator<int>::allocator() [75] std::vector<int, std::allocator<int> >::begin()
 [14] totalL()              [119] std::allocator<int>::~allocator() [39] std::vector<int, std::allocator<int> >::push_back(int const&)
  [2] CRO_step(double, void (*)()) [41] std::_Iter_base<double*, false>::_S_base(double*) [144] std::vector<int, std::allocator<int> >::vector()
 [10] vect::mag()            [24] std::_Iter_base<int*, false>::_S_base(int*) [145] std::vector<int, std::allocator<int> >::~vector()
 [13] vect::vect(double, double, double) [57] std::_Iter_base<std::move_iterator<double*>, true>::_S_base(std::move_iterator<double*>) [22] std::vector<int, std::allocator<int> >::operator[](unsigned int)
 [21] vect::vect()           [28] std::_Iter_base<std::move_iterator<int*>, true>::_S_base(std::move_iterator<int*>) [146] std::ios_base::precision(int)
 [11] vect::operator=(vect const&) [80] double* std::__copy_move<true, true, std::random_access_iterator_tag>::__copy_m<double>(double const*, double const*, double*) [59] std::_Miter_base<std::move_iterator<double*> >::iterator_type std::__miter_base<std::move_iterator<double*> >(std::move_iterator<double*>)
  [9] vect::operator-=(vect const&) [47] int* std::__copy_move<true, true, std::random_access_iterator_tag>::__copy_m<int>(int const*, int const*, int*) [30] std::_Miter_base<std::move_iterator<int*> >::iterator_type std::__miter_base<std::move_iterator<int*> >(std::move_iterator<int*>)
  [6] vect::operator*=(double const&) [120] void std::_Destroy_aux<false>::__destroy<std::string*>(std::string*, std::string*) [42] std::_Niter_base<double*>::iterator_type std::__niter_base<double*>(double*)
  [8] vect::operator-(vect const&) [88] void std::_Destroy_aux<true>::__destroy<double*>(double*, double*) [25] std::_Niter_base<int*>::iterator_type std::__niter_base<int*>(int*)
  [5] vect::operator*(double const&) [64] void std::_Destroy_aux<true>::__destroy<int*>(int*, int*) [82] double* std::__copy_move_a<true, double*, double*>(double*, double*, double*)
  [7] vect::operator+=(vect const&) [121] std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::_Vector_impl() [49] int* std::__copy_move_a<true, int*, int*>(int*, int*, int*)
 [12] vect::operator+(vect const&) [122] std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_impl::~_Vector_impl() [83] double* std::__copy_move_a2<true, double*, double*>(double*, double*, double*)
 [37] cobject::cobject()    [123] std::_Vector_base<std::string, std::allocator<std::string> >::_M_deallocate(std::string*, unsigned int) [50] int* std::__copy_move_a2<true, int*, int*>(int*, int*, int*)
[106] __gnu_cxx::new_allocator<std::string>::new_allocator() [124] std::_Vector_base<std::string, std::allocator<std::string> >::_M_get_Tp_allocator() [60] std::move_iterator<double*> std::make_move_iterator<double*>(double* const&)
[107] __gnu_cxx::new_allocator<std::string>::~new_allocator() [125] std::_Vector_base<std::string, std::allocator<std::string> >::_Vector_base() [31] std::move_iterator<int*> std::make_move_iterator<int*>(int* const&)
 [95] __gnu_cxx::new_allocator<double>::deallocate(double*, unsigned int) [126] std::_Vector_base<std::string, std::allocator<std::string> >::~_Vector_base() [84] double* std::uninitialized_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*)
 [96] __gnu_cxx::new_allocator<double>::allocate(unsigned int, void const*) [99] std::_Vector_base<double, std::allocator<double> >::_M_allocate(unsigned int) [51] int* std::uninitialized_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*)
[108] __gnu_cxx::new_allocator<double>::construct(double*, double const&) [127] std::_Vector_base<double, std::allocator<double> >::_Vector_impl::_Vector_impl() [85] double* std::__uninitialized_copy_a<std::move_iterator<double*>, double*, double>(std::move_iterator<double*>, std::move_iterator<double*>, double*, std::allocator<double>&)
[109] void __gnu_cxx::new_allocator<double>::construct<double>(double*, double&&) [128] std::_Vector_base<double, std::allocator<double> >::_Vector_impl::~_Vector_impl() [52] int* std::__uninitialized_copy_a<std::move_iterator<int*>, int*, int>(std::move_iterator<int*>, std::move_iterator<int*>, int*, std::allocator<int>&)
[110] __gnu_cxx::new_allocator<double>::new_allocator() [89] std::_Vector_base<double, std::allocator<double> >::_M_deallocate(double*, unsigned int) [86] double* std::__uninitialized_move_a<double*, double*, std::allocator<double> >(double*, double*, double*, std::allocator<double>&)
[111] __gnu_cxx::new_allocator<double>::~new_allocator() [61] std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() [53] int* std::__uninitialized_move_a<int*, int*, std::allocator<int> >(int*, int*, int*, std::allocator<int>&)
 [68] __gnu_cxx::new_allocator<int>::deallocate(int*, unsigned int) [129] std::_Vector_base<double, std::allocator<double> >::_Vector_base() [147] std::abs(double)
 [69] __gnu_cxx::new_allocator<int>::allocate(unsigned int, void const*) [130] std::_Vector_base<double, std::allocator<double> >::~_Vector_base() [62] unsigned int const& std::max<unsigned int>(unsigned int const&, unsigned int const&)
 [38] __gnu_cxx::new_allocator<int>::construct(int*, int const&) [72] std::_Vector_base<int, std::allocator<int> >::_M_allocate(unsigned int) [40] __gnu_cxx::__promote_2<__gnu_cxx::__enable_if<(std::__is_arithmetic<double>::__value)&&(std::__is_arithmetic<int>::__value), double>::__type, int>::__type std::pow<double, int>(double, int)
[112] __gnu_cxx::new_allocator<int>::new_allocator() [131] std::_Vector_base<int, std::allocator<int> >::_Vector_impl::_Vector_impl() [87] double* std::copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*)
[113] __gnu_cxx::new_allocator<int>::~new_allocator() [132] std::_Vector_base<int, std::allocator<int> >::_Vector_impl::~_Vector_impl() [54] int* std::copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*)
 [77] __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::__normal_iterator(double* const&) [65] std::_Vector_base<int, std::allocator<int> >::_M_deallocate(int*, unsigned int) [148] std::remove_reference<double&>::type&& std::move<double&>(double&&&)
 [43] __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::__normal_iterator(int* const&) [32] std::_Vector_base<int, std::allocator<int> >::_M_get_Tp_allocator() [149] double const&&& std::forward<double const&>(std::remove_reference<double const&>::type&)
 [97] __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::difference_type __gnu_cxx::operator-<double*, std::vector<double, std::allocator<double> > >(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&, __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > > const&) [133] std::_Vector_base<int, std::allocator<int> >::_Vector_base() [76] int const&&& std::forward<int const&>(std::remove_reference<int const&>::type&)
 [70] __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::difference_type __gnu_cxx::operator-<int*, std::vector<int, std::allocator<int> > >(__gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&, __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > > const&) [134] std::_Vector_base<int, std::allocator<int> >::~_Vector_base() [91] double&& std::forward<double>(std::remove_reference<double>::type&)
 [63] __gnu_cxx::new_allocator<double>::max_size() const [58] std::move_iterator<double*>::move_iterator(double*) [150] void std::_Destroy<std::string*>(std::string*, std::string*)
 [35] __gnu_cxx::new_allocator<int>::max_size() const [29] std::move_iterator<int*>::move_iterator(int*) [151] void std::_Destroy<std::string*, std::string>(std::string*, std::string*, std::allocator<std::string>&)
 [55] __gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >::base() const [81] double* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<double*>, double*>(std::move_iterator<double*>, std::move_iterator<double*>, double*) [92] void std::_Destroy<double*>(double*, double*)
 [26] __gnu_cxx::__normal_iterator<int*, std::vector<int, std::allocator<int> > >::base() const [48] int* std::__uninitialized_copy<true>::__uninit_copy<std::move_iterator<int*>, int*>(std::move_iterator<int*>, std::move_iterator<int*>, int*) [93] void std::_Destroy<double*, double>(double*, double*, std::allocator<double>&)
 [78] std::_Vector_base<double, std::allocator<double> >::_M_get_Tp_allocator() const [135] std::vector<std::string, std::allocator<std::string> >::vector() [66] void std::_Destroy<int*>(int*, int*)
 [44] std::_Vector_base<int, std::allocator<int> >::_M_get_Tp_allocator() const [136] std::vector<std::string, std::allocator<std::string> >::~vector() [67] void std::_Destroy<int*, int>(int*, int*, std::allocator<int>&)
 [56] std::move_iterator<double*>::base() const [137] void std::vector<double, std::allocator<double> >::emplace_back<double>(double&&) [33] bool std::operator==<char, std::char_traits<char>, std::allocator<char> >(std::basic_string<char, std::char_traits<char>, std::allocator<char> > const&, char const*)
 [27] std::move_iterator<int*>::base() const [138] void std::vector<double, std::allocator<double> >::_M_insert_aux<double const&>(__gnu_cxx::__normal_iterator<double*, std::vector<double, std::allocator<double> > >, double const&&&) [34] operator new(unsigned int, void*)

Introduction : GPU Benchmarking/Gaussian Blur Filter : Colin Paul

Cinque terre.jpgCinque terre BLURRED.jpg

convolution pattern
Plot of frequency response of the 2D Gaussian

What is Gaussian blurring?

At a high level, Gaussian blurring works just like box blurring in that there is a weight per pixel and that for each pixel, you apply the weights to that pixel and it’s neighbors to come up
with the final value for the blurred pixel. It uses a convolution pattern which is a linear stencil that applies fixed weights to the elements of a neighborhood in the combination operation.

With true Gaussian blurring however, the function that defines the weights for each pixel technically never reaches zero, but gets smaller and smaller over distance. In theory, this makes a
Gaussian kernel infinitely large. In practice though, you can choose a cut-off point and set the bounds.

The parameters to a Gaussian blur are:

  • Sigma (σ) – This defines how much blur there is. A larger number is a higher amount of blur.
  • Radius – The size of the kernel in pixels. The appropriate pixel size can be calculated for a specific sigma, but more information on that lower down.

Just like box blur, a Gaussian blur is separable which means that you can either apply a 2D convolution kernel, or you can apply a 1D convolution kernel on each axis. Doing a single 2D convolution
means more calculations, but you only need one buffer to put the results into. Doing two 1D convolutions (one on each axis), ends up being fewer calculations, but requires two buffers to put the results
into (one intermediate buffer to hold the first axis results).

Here is a 3 pixel 1D Gaussian Kernel for a sigma of 1.0:


1dkernel.png


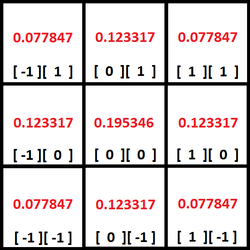
This kernel is useful for a two pass algorithm: First, perform a horizontal blur with the weights below and then perform a vertical blur on the resulting image (or vice versa).

Below is a 3×3 pixel 2D Gaussian Kernel also with a sigma of 1.0. Note that this can be calculated as an outer product (tensor product) of 1D kernels:


2dkernel.png


These weights below be used directly in a single pass blur algorithm: n2 samples per pixel.

An interesting property of Gaussian blurs is that you can apply multiple smaller blurs and it will come up with the result as if you did a larger Blur. Unfortunately it’s more
calculations doing multiple smaller blurs so is not usually worth while.

If you apply multiple blurs, the equivalent blur is the square root of the sum of the squares of the blur. Taking wikipedia’s example, if you applied a blur with radius 6 and a blur
with a radius of 8, you’d end up with the equivelant of a radius 10 blur. This is because √ ( 62 + 82 ) = 10

2D Gaussian

Calculating The Kernel

There are a couple ways to calculate a Gaussian kernel.

Pascal’s triangle approaches the Gaussian bell curve as the row number reaches infinity. Pascal’s triangle also represents the numbers that each term
is calculated by after expanding binomials (x + y)N. So technically, you could use a row from Pascal’s triangle as a 1D kernel and normalize the result, but it isn’t the most accurate.

A better way is to use the Gaussian function which is this: e-x2/(2 * σ2)

Where the sigma is your blur amount and x ranges across your values from the negative to the positive. For instance, if your kernel was 5 values, it would range from -2 to +2.

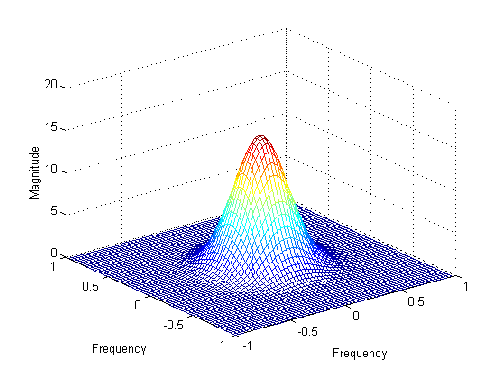
An even better way would be to integrate the Gaussian function instead of just taking point samples. Refer to the two graphs on the right.
The graphs plot the continuous distribution function and the discrete kernel approximation. One thing to look out for are the tails of the distribution vs. kernel weight:
For the current configuration, we have 13.36% of the curve’s area outside the discrete kernel. Note that the weights are renormalized such that the sum of all weights is one. Or in other words:
the probability mass outside the discrete kernel is redistributed evenly to all pixels within the kernel. The weights are calculated by numerical integration of the continuous gaussian distribution
over each discrete kernel tap.

Make sure to normalize the result so that the weights add up to 1. This makes sure that your blurring doesn’t make the image get brighter (greater than 1) or dimmer (less than 1).

Calculating The Kernel Size

Given a sigma value, you can calculate the size of the kernel you need by using this formula:1 + 2 √ ( -2σ2 ln 0.0005 )

That formula makes a Kernel large enough such that it cuts off when the value in the kernel is less than 0.5%. You can adjust the number in there to higher or lower depending on your desires for
speed versus quality.

Running the program

Code

[Expand] Windows source- Gassusan Blur Filter Main (Visual Studio) 
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <array>
#include <vector>
#include <functional>
#include <windows.h>  // for bitmap headers.

const float c_pi = 3.14159265359f;

struct SImageData
{
  SImageData()
    : m_width(0)
    , m_height(0)
  { }

  long m_width;
  long m_height;
  long m_pitch;
  std::vector<uint8_t> m_pixels;
};

void WaitForEnter()
{
  char c;
  std::cout << "Press Enter key to exit ... ";
  std::cin.get(c);
}

bool LoadImage(const char *fileName, SImageData& imageData)
{
  // open the file if we can
  FILE *file;
  file = fopen(fileName, "rb");
  if (!file)
    return false;

  // read the headers if we can
  BITMAPFILEHEADER header;
  BITMAPINFOHEADER infoHeader;
  if (fread(&header, sizeof(header), 1, file) != 1 ||
    fread(&infoHeader, sizeof(infoHeader), 1, file) != 1 ||
    header.bfType != 0x4D42 || infoHeader.biBitCount != 24)
  {
    fclose(file);
    return false;
  }

  // read in our pixel data if we can. Note that it's in BGR order, and width is padded to the next power of 4
  imageData.m_pixels.resize(infoHeader.biSizeImage);
  fseek(file, header.bfOffBits, SEEK_SET);
  if (fread(&imageData.m_pixels[0], imageData.m_pixels.size(), 1, file) != 1)
  {
    fclose(file);
    return false;
  }

  imageData.m_width = infoHeader.biWidth;
  imageData.m_height = infoHeader.biHeight;

  imageData.m_pitch = imageData.m_width * 3;
  if (imageData.m_pitch & 3)
  {
    imageData.m_pitch &= ~3;
    imageData.m_pitch += 4;
  }

  fclose(file);
  return true;
}

bool SaveImage(const char *fileName, const SImageData &image)
{
  // open the file if we can
  FILE *file;
  file = fopen(fileName, "wb");
  if (!file)
    return false;

  // make the header info
  BITMAPFILEHEADER header;
  BITMAPINFOHEADER infoHeader;

  header.bfType = 0x4D42;
  header.bfReserved1 = 0;
  header.bfReserved2 = 0;
  header.bfOffBits = 54;

  infoHeader.biSize = 40;
  infoHeader.biWidth = image.m_width;
  infoHeader.biHeight = image.m_height;
  infoHeader.biPlanes = 1;
  infoHeader.biBitCount = 24;
  infoHeader.biCompression = 0;
  infoHeader.biSizeImage = image.m_pixels.size();
  infoHeader.biXPelsPerMeter = 0;
  infoHeader.biYPelsPerMeter = 0;
  infoHeader.biClrUsed = 0;
  infoHeader.biClrImportant = 0;

  header.bfSize = infoHeader.biSizeImage + header.bfOffBits;

  // write the data and close the file
  fwrite(&header, sizeof(header), 1, file);
  fwrite(&infoHeader, sizeof(infoHeader), 1, file);
  fwrite(&image.m_pixels[0], infoHeader.biSizeImage, 1, file);
  fclose(file);
  return true;
}

int PixelsNeededForSigma(float sigma)
{
  // returns the number of pixels needed to represent a gaussian kernal that has values
  // down to the threshold amount.  A gaussian function technically has values everywhere
  // on the image, but the threshold lets us cut it off where the pixels contribute to
  // only small amounts that aren't as noticeable.
  const float c_threshold = 0.005f; // 0.5%
  return int(floor(1.0f + 2.0f * sqrtf(-2.0f * sigma * sigma * log(c_threshold)))) + 1;
}

float Gaussian(float sigma, float x)
{
  return expf(-(x*x) / (2.0f * sigma*sigma));
}

float GaussianSimpsonIntegration(float sigma, float a, float b)
{
  return
    ((b - a) / 6.0f) *
    (Gaussian(sigma, a) + 4.0f * Gaussian(sigma, (a + b) / 2.0f) + Gaussian(sigma, b));
}

std::vector<float> GaussianKernelIntegrals(float sigma, int taps)
{
  std::vector<float> ret;
  float total = 0.0f;
  for (int i = 0; i < taps; ++i)
  {
    float x = float(i) - float(taps / 2);
    float value = GaussianSimpsonIntegration(sigma, x - 0.5f, x + 0.5f);
    ret.push_back(value);
    total += value;
  }
  // normalize it
  for (unsigned int i = 0; i < ret.size(); ++i)
  {
    ret[i] /= total;
  }
  return ret;
}

const uint8_t* GetPixelOrBlack(const SImageData& image, int x, int y)
{
  static const uint8_t black[3] = { 0, 0, 0 };
  if (x < 0 || x >= image.m_width ||
    y < 0 || y >= image.m_height)
  {
    return black;
  }

  return &image.m_pixels[(y * image.m_pitch) + x * 3];
}

void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
{
  // allocate space for copying the image for destImage and tmpImage
  destImage.m_width = srcImage.m_width;
  destImage.m_height = srcImage.m_height;
  destImage.m_pitch = srcImage.m_pitch;
  destImage.m_pixels.resize(destImage.m_height * destImage.m_pitch);

  SImageData tmpImage;
  tmpImage.m_width = srcImage.m_width;
  tmpImage.m_height = srcImage.m_height;
  tmpImage.m_pitch = srcImage.m_pitch;
  tmpImage.m_pixels.resize(tmpImage.m_height * tmpImage.m_pitch);

  // horizontal blur from srcImage into tmpImage
  {
    auto row = GaussianKernelIntegrals(xblursigma, xblursize);

    int startOffset = -1 * int(row.size() / 2);

    for (int y = 0; y < tmpImage.m_height; ++y)
    {
      for (int x = 0; x < tmpImage.m_width; ++x)
      {
        std::array<float, 3> blurredPixel = { { 0.0f, 0.0f, 0.0f } };
        for (unsigned int i = 0; i < row.size(); ++i)
        {
          const uint8_t *pixel = GetPixelOrBlack(srcImage, x + startOffset + i, y);
          blurredPixel[0] += float(pixel[0]) * row[i];
          blurredPixel[1] += float(pixel[1]) * row[i];
          blurredPixel[2] += float(pixel[2]) * row[i];
        }

        uint8_t *destPixel = &tmpImage.m_pixels[y * tmpImage.m_pitch + x * 3];

        destPixel[0] = uint8_t(blurredPixel[0]);
        destPixel[1] = uint8_t(blurredPixel[1]);
        destPixel[2] = uint8_t(blurredPixel[2]);
      }
    }
  }

  // vertical blur from tmpImage into destImage
  {
    auto row = GaussianKernelIntegrals(yblursigma, yblursize);

    int startOffset = -1 * int(row.size() / 2);

    for (int y = 0; y < destImage.m_height; ++y)
    {
      for (int x = 0; x < destImage.m_width; ++x)
      {
        std::array<float, 3> blurredPixel = { { 0.0f, 0.0f, 0.0f } };
        for (unsigned int i = 0; i < row.size(); ++i)
        {
          const uint8_t *pixel = GetPixelOrBlack(tmpImage, x, y + startOffset + i);
          blurredPixel[0] += float(pixel[0]) * row[i];
          blurredPixel[1] += float(pixel[1]) * row[i];
          blurredPixel[2] += float(pixel[2]) * row[i];
        }

        uint8_t *destPixel = &destImage.m_pixels[y * destImage.m_pitch + x * 3];

        destPixel[0] = uint8_t(blurredPixel[0]);
        destPixel[1] = uint8_t(blurredPixel[1]);
        destPixel[2] = uint8_t(blurredPixel[2]);
      }
    }
  }
}

int main(int argc, char **argv)
{
  float xblursigma, yblursigma;

  bool showUsage = argc < 5 ||
    (sscanf(argv[3], "%f", &xblursigma) != 1) ||
    (sscanf(argv[4], "%f", &yblursigma) != 1);

  char *srcFileName = argv[1];
  char *destFileName = argv[2];

  if (showUsage)
  {
    printf("Usage: <source> <dest> <xblur> <yblur>\nBlur values are sigma\n\n");
    WaitForEnter();
    return 1;
  }

  // calculate pixel sizes, and make sure they are odd 
  int xblursize = PixelsNeededForSigma(xblursigma) | 1;
  int yblursize = PixelsNeededForSigma(yblursigma) | 1;

  printf("Attempting to blur a 24 bit image.\n");
  printf("  Source=%s\n  Dest=%s\n  blur=[%0.1f, %0.1f] px=[%d,%d]\n\n", srcFileName, destFileName, xblursigma, yblursigma, xblursize, yblursize);

  SImageData srcImage;
  if (LoadImage(srcFileName, srcImage))
  {
    printf("%s loaded\n", srcFileName);
    SImageData destImage;
    BlurImage(srcImage, destImage, xblursigma, yblursigma, xblursize, yblursize);
    if (SaveImage(destFileName, destImage))
      printf("Blurred image saved as %s\n", destFileName);
    else
    {
      printf("Could not save blurred image as %s\n", destFileName);
      WaitForEnter();
      return 1;
    }
  }
  else
  {
    printf("could not read 24 bit bmp file %s\n\n", srcFileName);
    WaitForEnter();
    return 1;
  }
  return 0;
}

Ported to Linux:

[Expand] Linux source - Gassusan Blur Filter Main (Command Line) 
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <math.h>
#include <array>
#include <vector>
#include <functional>
#include "windows.h"  // for bitmap headers.

/* uncomment the line below if you want to run grpof */
//#define RUN_GPROF

const float c_pi = 3.14159265359f;

struct SImageData
{
  SImageData()
    : m_width(0)
    , m_height(0)
  { }

  long m_width;
  long m_height;
  long m_pitch;
  std::vector<uint8_t> m_pixels;
};

void WaitForEnter()
{
  char c;
  std::cout << "Press Enter key to exit ... ";
  std::cin.get(c);
}

bool LoadImage(const char *fileName, SImageData& imageData)
{
  // open the file if we can
  FILE *file;
  file = fopen(fileName, "rb");
  if (!file)
    return false;

  // read the headers if we can
  BITMAPFILEHEADER header;
  BITMAPINFOHEADER infoHeader;
  if (fread(&header, sizeof(header), 1, file) != 1 ||
    fread(&infoHeader, sizeof(infoHeader), 1, file) != 1 ||
    header.bfType != 0x4D42 || infoHeader.biBitCount != 24)
  {
    fclose(file);
    return false;
  }

  // read in our pixel data if we can. Note that it's in BGR order, and width is padded to the next power of 4
  imageData.m_pixels.resize(infoHeader.biSizeImage);
  fseek(file, header.bfOffBits, SEEK_SET);
  if (fread(&imageData.m_pixels[0], imageData.m_pixels.size(), 1, file) != 1)
  {
    fclose(file);
    return false;
  }

  imageData.m_width = infoHeader.biWidth;
  imageData.m_height = infoHeader.biHeight;

  imageData.m_pitch = imageData.m_width * 3;
  if (imageData.m_pitch & 3)
  {
    imageData.m_pitch &= ~3;
    imageData.m_pitch += 4;
  }

  fclose(file);
  return true;
}

bool SaveImage(const char *fileName, const SImageData &image)
{
  // open the file if we can
  FILE *file;
  file = fopen(fileName, "wb");
  if (!file)
    return false;

  // make the header info
  BITMAPFILEHEADER header;
  BITMAPINFOHEADER infoHeader;

  header.bfType = 0x4D42;
  header.bfReserved1 = 0;
  header.bfReserved2 = 0;
  header.bfOffBits = 54;

  infoHeader.biSize = 40;
  infoHeader.biWidth = image.m_width;
  infoHeader.biHeight = image.m_height;
  infoHeader.biPlanes = 1;
  infoHeader.biBitCount = 24;
  infoHeader.biCompression = 0;
  infoHeader.biSizeImage = image.m_pixels.size();
  infoHeader.biXPelsPerMeter = 0;
  infoHeader.biYPelsPerMeter = 0;
  infoHeader.biClrUsed = 0;
  infoHeader.biClrImportant = 0;

  header.bfSize = infoHeader.biSizeImage + header.bfOffBits;

  // write the data and close the file
  fwrite(&header, sizeof(header), 1, file);
  fwrite(&infoHeader, sizeof(infoHeader), 1, file);
  fwrite(&image.m_pixels[0], infoHeader.biSizeImage, 1, file);
  fclose(file);
  return true;
}

int PixelsNeededForSigma(float sigma)
{
  // returns the number of pixels needed to represent a gaussian kernal that has values
  // down to the threshold amount.  A gaussian function technically has values everywhere
  // on the image, but the threshold lets us cut it off where the pixels contribute to
  // only small amounts that aren't as noticeable.
  const float c_threshold = 0.005f; // 0.5%
  return int(floor(1.0f + 2.0f * sqrtf(-2.0f * sigma * sigma * log(c_threshold)))) + 1;
}

float Gaussian(float sigma, float x)
{
  return expf(-(x*x) / (2.0f * sigma*sigma));
}

float GaussianSimpsonIntegration(float sigma, float a, float b)
{
  return
    ((b - a) / 6.0f) *
    (Gaussian(sigma, a) + 4.0f * Gaussian(sigma, (a + b) / 2.0f) + Gaussian(sigma, b));
}

std::vector<float> GaussianKernelIntegrals(float sigma, int taps)
{
  std::vector<float> ret;
  float total = 0.0f;
  for (int i = 0; i < taps; ++i)
  {
    float x = float(i) - float(taps / 2);
    float value = GaussianSimpsonIntegration(sigma, x - 0.5f, x + 0.5f);
    ret.push_back(value);
    total += value;
  }
  // normalize it
  for (unsigned int i = 0; i < ret.size(); ++i)
  {
    ret[i] /= total;
  }
  return ret;
}

const uint8_t* GetPixelOrBlack(const SImageData& image, int x, int y)
{
  static const uint8_t black[3] = { 0, 0, 0 };
  if (x < 0 || x >= image.m_width ||
    y < 0 || y >= image.m_height)
  {
    return black;
  }

  return &image.m_pixels[(y * image.m_pitch) + x * 3];
}

void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
{
  // allocate space for copying the image for destImage and tmpImage
  destImage.m_width = srcImage.m_width;
  destImage.m_height = srcImage.m_height;
  destImage.m_pitch = srcImage.m_pitch;
  destImage.m_pixels.resize(destImage.m_height * destImage.m_pitch);

  SImageData tmpImage;
  tmpImage.m_width = srcImage.m_width;
  tmpImage.m_height = srcImage.m_height;
  tmpImage.m_pitch = srcImage.m_pitch;
  tmpImage.m_pixels.resize(tmpImage.m_height * tmpImage.m_pitch);

  // horizontal blur from srcImage into tmpImage
  {
    auto row = GaussianKernelIntegrals(xblursigma, xblursize);

    int startOffset = -1 * int(row.size() / 2);

    for (int y = 0; y < tmpImage.m_height; ++y)
    {
      for (int x = 0; x < tmpImage.m_width; ++x)
      {
        std::array<float, 3> blurredPixel = { { 0.0f, 0.0f, 0.0f } };
        for (unsigned int i = 0; i < row.size(); ++i)
        {
          const uint8_t *pixel = GetPixelOrBlack(srcImage, x + startOffset + i, y);
          blurredPixel[0] += float(pixel[0]) * row[i];
          blurredPixel[1] += float(pixel[1]) * row[i];
          blurredPixel[2] += float(pixel[2]) * row[i];
        }

        uint8_t *destPixel = &tmpImage.m_pixels[y * tmpImage.m_pitch + x * 3];

        destPixel[0] = uint8_t(blurredPixel[0]);
        destPixel[1] = uint8_t(blurredPixel[1]);
        destPixel[2] = uint8_t(blurredPixel[2]);
      }
    }
  }

  // vertical blur from tmpImage into destImage
  {
    auto row = GaussianKernelIntegrals(yblursigma, yblursize);

    int startOffset = -1 * int(row.size() / 2);

    for (int y = 0; y < destImage.m_height; ++y)
    {
      for (int x = 0; x < destImage.m_width; ++x)
      {
        std::array<float, 3> blurredPixel = { { 0.0f, 0.0f, 0.0f } };
        for (unsigned int i = 0; i < row.size(); ++i)
        {
          const uint8_t *pixel = GetPixelOrBlack(tmpImage, x, y + startOffset + i);
          blurredPixel[0] += float(pixel[0]) * row[i];
          blurredPixel[1] += float(pixel[1]) * row[i];
          blurredPixel[2] += float(pixel[2]) * row[i];
        }

        uint8_t *destPixel = &destImage.m_pixels[y * destImage.m_pitch + x * 3];

        destPixel[0] = uint8_t(blurredPixel[0]);
        destPixel[1] = uint8_t(blurredPixel[1]);
        destPixel[2] = uint8_t(blurredPixel[2]);
      }
    }
  }
}

int main(int argc, char **argv)
{

#ifdef RUN_GPROF

  float xblursigma = 3.0f, yblursigma = 3.0f;

  bool showUsage = false;

  const char *srcFileName = "cinque_terre.bmp";
  const char *destFileName = "cinque_terre_BLURRED.bmp";

#else

  float xblursigma, yblursigma;

  bool showUsage = argc < 5 ||
    (sscanf(argv[3], "%f", &xblursigma) != 1) ||
    (sscanf(argv[4], "%f", &yblursigma) != 1);

  char *srcFileName = argv[1];
  char *destFileName = argv[2];

#endif /* RUN_GPROF */

  if (showUsage)
  {
    printf("Usage: <source> <dest> <xblur> <yblur>\nBlur values are sigma\n\n");
    WaitForEnter();
    return 1;
  }

  // calculate pixel sizes, and make sure they are odd
  int xblursize = PixelsNeededForSigma(xblursigma) | 1;
  int yblursize = PixelsNeededForSigma(yblursigma) | 1;

  printf("Attempting to blur a 24 bit image.\n");
  printf("  Source=%s\n  Dest=%s\n  blur=[%0.1f, %0.1f] px=[%d,%d]\n\n", srcFileName, destFileName, xblursigma, yblursigma, xblursize, yblursize);

  SImageData srcImage;
  if (LoadImage(srcFileName, srcImage))
  {
    printf("%s loaded\n", srcFileName);
    SImageData destImage;
    BlurImage(srcImage, destImage, xblursigma, yblursigma, xblursize, yblursize);
    if (SaveImage(destFileName, destImage))
      printf("Blurred image saved as %s\n", destFileName);
    else
    {
      printf("Could not save blurred image as %s\n", destFileName);
      WaitForEnter();
      return 1;
    }
  }
  else
  {
    printf("could not read 24 bit bmp file %s\n\n", srcFileName);
    WaitForEnter();
    return 1;
  }
  return 0;
}
[Expand] Linux source - Gassusan Blur Filter Header (Linux cannot use Windows API, replicated the required structs. Ref: MSDN 12) 
#pragma once

// for Linux platform, please make sure the size of data type is correct for BMP spec.
// if you use this on Windows or other platforms, please pay attention to this.
typedef int LONG;
typedef unsigned char BYTE;
typedef unsigned int DWORD;
typedef unsigned short WORD;

// __attribute__((packed)) on non-Intel architecture may cause some unexpected errors!

typedef struct tagBITMAPFILEHEADER
{
    WORD    bfType;             // 2  /* File type */
    DWORD   bfSize;             // 4  /* File size in bytes */
    WORD    bfReserved1;        // 2
    WORD    bfReserved2;        // 2
    DWORD   bfOffBits;          // 4 /* Offset to image data, bytes */
} __attribute__((packed)) BITMAPFILEHEADER;

typedef struct tagBITMAPINFOHEADER
{
    DWORD    biSize;            // 4 /* Header size in bytes */
    LONG     biWidth;           // 4 /* Width of image */
    LONG     biHeight;          // 4 /* Height of image */
    WORD     biPlanes;          // 2 /* Number of colour planes */
    WORD     biBitCount;        // 2 /* Bits per pixel */
    DWORD    biCompression;     // 4 /* Compression type */
    DWORD    biSizeImage;       // 4 /* Image size in bytes */
    LONG     biXPelsPerMeter;   // 4
    LONG     biYPelsPerMeter;   // 4 /* Pixels per meter */
    DWORD    biClrUsed;         // 4 /* Number of colours */
    DWORD    biClrImportant;    // 4 /* Important colours */
} __attribute__((packed)) BITMAPINFOHEADER;

Windows

To compile and run the program:

  1. Set-up an empty Visual C++ - Visual Studio project.
  2. Save this image and place it in your projects directory.
  3. Copy the Windows version of the main source code above and paste it into a [your chosen file name].cpp file.
  4. Go into you Debug properties of your project.
  5. Add four (4) values into the Debugging -> Command Arguments (outlined below)
  6. Run in Release x64

The command line arguments are structured as follows: 

[input image filename].bmp [output image filename].bmp [x - sigma value] [y - sigmea value] => cinque_terre.bmp cinque_terre_BLURRED.bmp 3.0 3.0

Linux

To compile and run the program:

  1. Navigate to the directory you want to run the program in.
  2. Save this image and place it into the directory you will be running the program from.
  3. Copy the Linux version of the main source code above and paste it into a [your chosen file name].cpp file.
  4. Copy the Linux version of the header source code above and paste it into a file named windows.h.

Compile the binaries using the following command: 

g++ -O2 -std=c++0x -Wall -pedantic [your chosen file name].cpp -o gblur

The command line arguments are structured as follows: 

[input image filename].bmp [output image filename].bmp [x - sigma value] [y - sigmea value]

Run the compiled program with the required arguments 

./gblur cinque_terre.bmp cinque_terre_BLURRED.bmp 3.0 3.0

Mac OS X

To compile and run the program:

  1. Navigate to the directory you want to run the program in.
  2. Save this image and place it into the directory you will be running the program from.
  3. Copy the Linux version of the main source code above and paste it into a [your chosen file name].cpp file.
  4. Copy the Linux version of the header source code above and paste it into a file named windows.h.

Compile the binaries using the following command: 

clang++ -O2 -std=c++0x -Wall -pedantic [your chosen file name].cpp -o gblur

The command line arguments are structured as follows: 

[input image filename].bmp [output image filename].bmp [x - sigma value] [y - sigmea value]

Run the compiled program with the required arguments 

./gblur cinque_terre.bmp cinque_terre_BLURRED.bmp 3.0 3.0

Analysis

Flat profile:

Each sample counts as 0.01 seconds.
  %   cumulative   self              self     total
 time   seconds   seconds    calls  ns/call  ns/call  name
 61.38      3.37     3.37                             BlurImage(SImageData const&, SImageData&, float, float, unsigned int, unsigned int)
 38.62      5.49     2.12 172032000    12.32    12.32  GetPixelOrBlack(SImageData const&, int, int)
  0.00      5.49     0.00      126     0.00     0.00  Gaussian(float, float)
  0.00      5.49     0.00       42     0.00     0.00  GaussianSimpsonIntegration(float, float, float)
  0.00      5.49     0.00       12     0.00     0.00  void std::vector<float, std::allocator<float> >::_M_insert_aux<float const&>(__gnu_cxx::__normal_iterator<float*, std::vector<float, std::allocator<float> > >, float const&&&)
  0.00      5.49     0.00        3     0.00     0.00  std::vector<unsigned char, std::allocator<unsigned char> >::_M_default_append(unsigned int)
  0.00      5.49     0.00        2     0.00     0.00  GaussianKernelIntegrals(float, int)
  0.00      5.49     0.00        1     0.00     0.00  _GLOBAL__sub_I__Z12WaitForEnterv

Call graph:


granularity: each sample hit covers 4 byte(s) for 0.18% of 5.49 seconds

index % time    self  children    called     name
                                                <spontaneous>
[1]    100.0    3.37    2.12                 BlurImage(SImageData const&, SImageData&, float, float, unsigned int, unsigned int) [1]
                2.12    0.00 172032000/172032000     GetPixelOrBlack(SImageData const&, int, int) [2]
                0.00    0.00       2/2           GaussianKernelIntegrals(float, int) [11]
                0.00    0.00       2/3           std::vector<unsigned char, std::allocator<unsigned char> >::_M_default_append(unsigned int) [10]
-----------------------------------------------
                2.12    0.00 172032000/172032000     BlurImage(SImageData const&, SImageData&, float, float, unsigned int, unsigned int) [1]
[2]     38.6    2.12    0.00 172032000         GetPixelOrBlack(SImageData const&, int, int) [2]
-----------------------------------------------
                0.00    0.00     126/126         GaussianSimpsonIntegration(float, float, float) [8]
[7]      0.0    0.00    0.00     126         Gaussian(float, float) [7]
-----------------------------------------------
                0.00    0.00      42/42          GaussianKernelIntegrals(float, int) [11]
[8]      0.0    0.00    0.00      42         GaussianSimpsonIntegration(float, float, float) [8]
                0.00    0.00     126/126         Gaussian(float, float) [7]
-----------------------------------------------
                0.00    0.00      12/12          GaussianKernelIntegrals(float, int) [11]
[9]      0.0    0.00    0.00      12         void std::vector<float, std::allocator<float> >::_M_insert_aux<float const&>(__gnu_cxx::__normal_iterator<float*, std::vector<float, std::allocator<float> > >, float const&&&) [9]
-----------------------------------------------
                0.00    0.00       1/3           LoadImage(char const*, SImageData&) [15]
                0.00    0.00       2/3           BlurImage(SImageData const&, SImageData&, float, float, unsigned int, unsigned int) [1]
[10]     0.0    0.00    0.00       3         std::vector<unsigned char, std::allocator<unsigned char> >::_M_default_append(unsigned int) [10]
-----------------------------------------------
                0.00    0.00       2/2           BlurImage(SImageData const&, SImageData&, float, float, unsigned int, unsigned int) [1]
[11]     0.0    0.00    0.00       2         GaussianKernelIntegrals(float, int) [11]
                0.00    0.00      42/42          GaussianSimpsonIntegration(float, float, float) [8]
                0.00    0.00      12/12          void std::vector<float, std::allocator<float> >::_M_insert_aux<float const&>(__gnu_cxx::__normal_iterator<float*, std::vector<float, std::allocator<float> > >, float const&&&) [9]
-----------------------------------------------
                0.00    0.00       1/1           __do_global_ctors_aux [18]
[12]     0.0    0.00    0.00       1         _GLOBAL__sub_I__Z12WaitForEnterv [12]
-----------------------------------------------

Index by function name

  [12] _GLOBAL__sub_I__Z12WaitForEnterv (gaussian.cpp) [8] GaussianSimpsonIntegration(float, float, float) [9] void std::vector<float, std::allocator<float> >::_M_insert_aux<float const&>(__gnu_cxx::__normal_iterator<float*, std::vector<float, std::allocator<float> > >, float const&&&)
   [2] GetPixelOrBlack(SImageData const&, int, int) [7] Gaussian(float, float) [10] std::vector<unsigned char, std::allocator<unsigned char> >::_M_default_append(unsigned int)
  [11] GaussianKernelIntegrals(float, int) [1] BlurImage(SImageData const&, SImageData&, float, float, unsigned int, unsigned int)

Observations

The program does not take a long time to run, but run-time depends on the values of sigma (σ) and the kernel block size. If you specify larger values for these parameters the runtime increases
significantly. The code is straight forward and parallelization should be easy to implement.

Hotspot

[Expand] Culptit - BlurImage( ... ) 
void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
{

  // ...

  {
    auto row = GaussianKernelIntegrals(xblursigma, xblursize);

    // ...

    for (int y = 0; y < tmpImage.m_height; ++y)
    {
      for (int x = 0; x < tmpImage.m_width; ++x)
      {

        // ...

        for (unsigned int i = 0; i < row.size(); ++i)
        {
          const uint8_t *pixel = GetPixelOrBlack(srcImage, x + startOffset + i, y);

          // ...

        }

        // ...

      }
    }
  }

  {
    auto row = GaussianKernelIntegrals(yblursigma, yblursize);

    // ...

    for (int y = 0; y < destImage.m_height; ++y)
    {
      for (int x = 0; x < destImage.m_width; ++x)
      {

        // ...

        for (unsigned int i = 0; i < row.size(); ++i)
        {
          const uint8_t *pixel = GetPixelOrBlack(tmpImage, x, y + startOffset + i);

          // ...

        }

        // ...

      }
    }
  }
}

According to the Flat profile, 61.38% of the time is spent in the BlurImage function. This function contains a set of triply-nested for-loops which equates to a run-time of T(n) is O(n3).
Referring to the Call graph we can see more supporting evidence that this application spends nearly all of its execution time in the BlurImage function. Therefore this function is the prime candidate
for parallelization using CUDA. The sigma (σ) and the kernel size can be increased in order to make the computation stressful on the GPU to get a significant benchmark.

Assignment 2/3 - Parallelize & Optimize

* For gaussian blur we say it's unoptimized because we feel that there is more that can be done to reduce the execution times.
  The code displayed in the code snippets does use CUDA parallel constructs and fine tuning techniques such as streaming - async.

Gaussian Blur

[Expand] Unoptimized* - BlurImage( ... ) 
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <array>
#include <vector>
#include <functional>
#include <windows.h>  // for bitmap headers.
#include <algorithm>
#include <chrono>

#include <cuda_runtime.h>
// to remove intellisense highlighting
#include <device_launch_parameters.h>
#include <device_functions.h>

//#ifdef __CUDACC__
//#if __CUDACC_VER_MAJOR__ == 1
//const int ntpb = 512;
//#else
//const int ntpb = 1024;
//#endif
//#endif
const int ntpb = 1024;
const int STREAMS = 32;

void check(cudaError_t error) {
	if (error != cudaSuccess) {
		throw std::exception(cudaGetErrorString(error));
	}
}

struct SImageData
{
	SImageData()
		: m_width(0)
		, m_height(0)
	{ }

	long m_width;
	long m_height;
	long m_pitch;
	std::vector<uint8_t> m_pixels;
};

void WaitForEnter()
{
	char c;
	std::cout << "Press Enter key to exit ... ";
	std::cin.get(c);
}

bool LoadImage(const char *fileName, SImageData& imageData)
{
	// open the file if we can
	FILE *file;
	file = fopen(fileName, "rb");
	if (!file)
		return false;

	// read the headers if we can
	BITMAPFILEHEADER header;
	BITMAPINFOHEADER infoHeader;
	if (fread(&header, sizeof(header), 1, file) != 1 ||
		fread(&infoHeader, sizeof(infoHeader), 1, file) != 1 ||
		header.bfType != 0x4D42 || infoHeader.biBitCount != 24)
	{
		fclose(file);
		return false;
	}

	// read in our pixel data if we can. Note that it's in BGR order, and width is padded to the next power of 4
	imageData.m_pixels.resize(infoHeader.biSizeImage);
	fseek(file, header.bfOffBits, SEEK_SET);
	if (fread(&imageData.m_pixels[0], imageData.m_pixels.size(), 1, file) != 1)
	{
		fclose(file);
		return false;
	}

	imageData.m_width = infoHeader.biWidth;
	imageData.m_height = infoHeader.biHeight;

	imageData.m_pitch = imageData.m_width * 3;
	if (imageData.m_pitch & 3)
	{
		imageData.m_pitch &= ~3;
		imageData.m_pitch += 4;
	}

	fclose(file);
	return true;
}

bool SaveImage(const char *fileName, const SImageData &image)
{
	// open the file if we can
	FILE *file;
	file = fopen(fileName, "wb");
	if (!file)
		return false;

	// make the header info
	BITMAPFILEHEADER header;
	BITMAPINFOHEADER infoHeader;

	header.bfType = 0x4D42;
	header.bfReserved1 = 0;
	header.bfReserved2 = 0;
	header.bfOffBits = 54;

	infoHeader.biSize = 40;
	infoHeader.biWidth = image.m_width;
	infoHeader.biHeight = image.m_height;
	infoHeader.biPlanes = 1;
	infoHeader.biBitCount = 24;
	infoHeader.biCompression = 0;
	infoHeader.biSizeImage = image.m_pixels.size();
	infoHeader.biXPelsPerMeter = 0;
	infoHeader.biYPelsPerMeter = 0;
	infoHeader.biClrUsed = 0;
	infoHeader.biClrImportant = 0;

	header.bfSize = infoHeader.biSizeImage + header.bfOffBits;

	// write the data and close the file
	fwrite(&header, sizeof(header), 1, file);
	fwrite(&infoHeader, sizeof(infoHeader), 1, file);
	fwrite(&image.m_pixels[0], infoHeader.biSizeImage, 1, file);
	fclose(file);
	return true;
}

int PixelsNeededForSigma(float sigma)
{
	// returns the number of pixels needed to represent a gaussian kernal that has values
	// down to the threshold amount.  A gaussian function technically has values everywhere
	// on the image, but the threshold lets us cut it off where the pixels contribute to
	// only small amounts that aren't as noticeable.
	const float c_threshold = 0.005f; // 0.5%
	return int(floor(1.0f + 2.0f * sqrtf(-2.0f * sigma * sigma * log(c_threshold)))) + 1;
}

float Gaussian(float sigma, float x)
{
	return expf(-(x*x) / (2.0f * sigma*sigma));
}

float GaussianSimpsonIntegration(float sigma, float a, float b)
{
	return
		((b - a) / 6.0f) *
		(Gaussian(sigma, a) + 4.0f * Gaussian(sigma, (a + b) / 2.0f) + Gaussian(sigma, b));
}

std::vector<float> GaussianKernelIntegrals(float sigma, int taps)
{
	std::vector<float> ret;
	float total = 0.0f;
	for (int i = 0; i < taps; ++i)
	{
		float x = float(i) - float(taps / 2);
		float value = GaussianSimpsonIntegration(sigma, x - 0.5f, x + 0.5f);
		ret.push_back(value);
		total += value;
	}
	// normalize it
	for (unsigned int i = 0; i < ret.size(); ++i)
	{
		ret[i] /= total;
	}
	return ret;
}

struct BGRPixel {
	float b;
	float g;
	float r;
};

__global__ void blur_kernel(BGRPixel* imageIn, BGRPixel* imageOut, float* blur, int n_blur, int x, int start, int jump) {
	int idx = blockDim.x*blockIdx.x + threadIdx.x;	// Location on the row

	if (idx < x) {
		int id = start + idx;
		int bstart = id - (n_blur / 2)*jump;

		BGRPixel pixel{ 0.0f, 0.0f, 0.0f };

		for (int i = 0; i < n_blur; ++i) {
			int bid = bstart + i*jump;
			float iblur = blur[i];

			pixel.b += imageIn[bid].b * iblur;
			pixel.g += imageIn[bid].g * iblur;
			pixel.r += imageIn[bid].r * iblur;
		}

		imageOut[id].b = pixel.b;
		imageOut[id].g = pixel.g;
		imageOut[id].r = pixel.r;
	}
}

void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
{
	int xImage = srcImage.m_width;							// Width of image
	int yImage = srcImage.m_height;							// Height of image
	int imageSize = xImage*yImage;

	int xPadded = xImage + (xblursize - 1);					// Width including padding
	int yPadded = yImage + (yblursize - 1);					// Height including padding
	int paddedSize = xPadded*yPadded;

	int xPad = xblursize / 2;								// Number of padding columns on each side
	int yPad = yblursize / 2;
	int padOffset = xPadded*yPad + xPad;							// Offset to first pixel in padded image

	float* pinnedImage = nullptr;
	BGRPixel* d_padded1 = nullptr;
	BGRPixel* d_padded2 = nullptr;

	float*	d_xblur = nullptr;					// XBlur integrals
	int		n_xblur;							// N

	float*	d_yblur = nullptr;					// YBlur integrals
	int		n_yblur;							// N

	// Allocate memory for host and device
	check(cudaHostAlloc((void**)&pinnedImage, 3 * imageSize * sizeof(float), 0));
	check(cudaMalloc((void**)&d_padded1, paddedSize * sizeof(BGRPixel)));
	check(cudaMalloc((void**)&d_padded2, paddedSize * sizeof(BGRPixel)));

	// Copy image to pinned memory
	for (int i = 0; i < 3 * imageSize; ++i) {
		pinnedImage[i] = (float)srcImage.m_pixels[i];
	}

	// Allocate and assign intergrals
	{
		auto row_blur = GaussianKernelIntegrals(xblursigma, xblursize);
		auto col_blur = GaussianKernelIntegrals(yblursigma, yblursize);

		// ROW
		n_xblur = row_blur.size();
		check(cudaMalloc((void**)&d_xblur, n_xblur * sizeof(float)));
		check(cudaMemcpy(d_xblur, row_blur.data(), n_xblur * sizeof(float), cudaMemcpyHostToDevice));

		// COLUMN
		n_yblur = col_blur.size();
		check(cudaMalloc((void**)&d_yblur, n_yblur * sizeof(float)));
		check(cudaMemcpy(d_yblur, col_blur.data(), n_yblur * sizeof(float), cudaMemcpyHostToDevice));
	}


	cudaStream_t stream[STREAMS];

	int nblks = (xImage + (ntpb - 1)) / ntpb;

	for (int i = 0; i < STREAMS; ++i) {
		check(cudaStreamCreate(&stream[i]));
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			cudaMemcpyAsync(d_padded1 + padOffset + i*xPadded, pinnedImage + (3 * i*xImage), 3 * xImage * sizeof(float), cudaMemcpyHostToDevice, stream[j]);
		}
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded1, d_padded2, d_xblur, n_xblur, xImage, padOffset + i*xPadded, 1);
		}
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded2, d_padded1, d_yblur, n_yblur, xImage, padOffset + i*xPadded, xPadded);
		}
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			check(cudaMemcpyAsync(pinnedImage + (3 * i*xImage), d_padded1 + padOffset + i*xPadded, xImage * sizeof(BGRPixel), cudaMemcpyDeviceToHost, stream[j]));
		}
	}

	for (int i = 0; i < STREAMS; ++i) {
		check(cudaStreamSynchronize(stream[i]));
		check(cudaStreamDestroy(stream[i]));
	}

	destImage.m_width = srcImage.m_width;
	destImage.m_height = srcImage.m_height;
	destImage.m_pitch = srcImage.m_pitch;
	destImage.m_pixels.resize(srcImage.m_pixels.size());

	for (int i = 0; i < 3 * imageSize; i++) {
		destImage.m_pixels[i] = (uint8_t)pinnedImage[i];
	};

	check(cudaFree(d_xblur));
	check(cudaFree(d_yblur));

	check(cudaFreeHost(pinnedImage));
	check(cudaFree(d_padded1));
	check(cudaFree(d_padded2));

	check(cudaDeviceReset());
}

int main(int argc, char **argv)
{
	float xblursigma, yblursigma;

	bool showUsage = argc < 5 ||
		(sscanf(argv[3], "%f", &xblursigma) != 1) ||
		(sscanf(argv[4], "%f", &yblursigma) != 1);

	char *srcFileName = argv[1];
	char *destFileName = argv[2];

	if (showUsage)
	{
		printf("Usage: <source> <dest> <xblur> <yblur>\nBlur values are sigma\n\n");
		WaitForEnter();
		return 1;
	}

	// calculate pixel sizes, and make sure they are odd 
	int xblursize = PixelsNeededForSigma(xblursigma) | 1;
	int yblursize = PixelsNeededForSigma(yblursigma) | 1;

	printf("Attempting to blur a 24 bit image.\n");
	printf("  Source=%s\n  Dest=%s\n  blur=[%0.1f, %0.1f] px=[%d,%d]\n\n", srcFileName, destFileName, xblursigma, yblursigma, xblursize, yblursize);

	SImageData srcImage;
	if (LoadImage(srcFileName, srcImage))
	{
		printf("%s loaded\n", srcFileName);
		SImageData destImage;

		auto t1 = std::chrono::high_resolution_clock::now();
		BlurImage(srcImage, destImage, xblursigma, yblursigma, xblursize, yblursize);
		auto t2 = std::chrono::high_resolution_clock::now();

		std::cout << "BlurImage time: " << std::chrono::duration_cast<std::chrono::microseconds>(t2 - t1).count() << "us" << std::endl;


		if (SaveImage(destFileName, destImage))
			printf("Blurred image saved as %s\n", destFileName);
		else
		{
			printf("Could not save blurred image as %s\n", destFileName);
			WaitForEnter();
			return 1;
		}
	}
	else
	{
		printf("could not read 24 bit bmp file %s\n\n", srcFileName);
		WaitForEnter();
		return 1;
	}
	return 0;
}

Objectives

The main objective was to not change the main function. This objective was met, although code had to be added for profiling.

Steps

Host Memory Management

In the original program a bmp is loaded into an vector of uint8_t. This is not ideal for CUDA, therefore an array of pinned memory was allocated. This array contains the same amount of elements but stores them as a structure, "BGRPixel" which is three contiguous floats. The vector is then transferred over to pinned memory.

[Expand] Host Memory Management - Code( ... ) 
struct SImageData
{
	SImageData()
		: m_width(0)
		, m_height(0)
	{ }

	long m_width;
	long m_height;
	long m_pitch;
	std::vector<uint8_t> m_pixels;
};

struct BGRPixel {
	float b;
	float g;
	float r;
};


void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
{
	int xImage = srcImage.m_width;							// Width of image
	int yImage = srcImage.m_height;							// Height of image
	int imageSize = xImage*yImage;

	int xPadded = xImage + (xblursize - 1);					// Width including padding
	int yPadded = yImage + (yblursize - 1);					// Height including padding
	int paddedSize = xPadded*yPadded;

	int xPad = xblursize / 2;								// Number of padding columns on each side
	int yPad = yblursize / 2;
	int padOffset = xPadded*yPad + xPad;							// Offset to first pixel in padded image

	float* pinnedImage = nullptr;
	BGRPixel* d_padded1 = nullptr;
	BGRPixel* d_padded2 = nullptr;

        // ...

	// Allocate memory for host and device
	check(cudaHostAlloc((void**)&pinnedImage, 3 * imageSize * sizeof(float), 0));
	check(cudaMalloc((void**)&d_padded1, paddedSize * sizeof(BGRPixel)));
	check(cudaMalloc((void**)&d_padded2, paddedSize * sizeof(BGRPixel)));

	// Copy image to pinned memory
	for (int i = 0; i < 3 * imageSize; ++i) {
		pinnedImage[i] = (float)srcImage.m_pixels[i];
	}

        // ...
}

Device Memory Management

To get a blurred pixel the surrounding pixels must be sampled, in some cases this means sampling pixels outside the bounds of the image. In the original, a simple if check was used to determine if the pixel was outside the bounds or the image, if it was a black pixel was returned instead. This if statement most likely would have caused massive thread divergence in a kernel, therefore the images created in device memory featured additional padding of black pixels to compensate for this. Two such images were created, one to perform horizontal blur and one to perform vertical blur. Other small device arrays were also needed to store the Gaussian integrals that are used to produce the blurring effect.

[Expand] Padding example

Shrunk.png

Pad.png


This is how the image would be padded for 3x3 sigma blur.

The original image is 2560x1600 -> 11.7MB

With blur sigmas [x = 3, y = 3] and conversion to float the padded images will be 2600x1640 -> 48.8MB

Increase of 4.1% pixels and with the conversion for uint8_t to float total increase of 317% in memory requirements on the GPU

Since two padded images are needed at least 97.6MB will be on the GPU

Host to Device

To copy the pinned image to the device an array of streams was used to asynchronously copy each row of the image over. Doing so allowed the rows to be easily copied over while avoiding infringing on the extra padding pixels.

Kernels

First one image is blurred horizontally. One image is used as a reference while the other is written to. Kernels are also executed using the streams, so that each stream will blur a single row at a time. After the horizontal blur is finished the vertical blur is launched in the same manner, except that the previously written to image is used as a reference while the previous reference is now written to. The two blur are able to use the same kernel due to the fact that the pixel sampling technique works by iterating through pixels because of this the step size can be changed to sample across the row or down the column.

Device to Host

After that is done the image is copied back using the streams in the same way it was copied over.

Code

[Expand] Unoptimized* - BlurImage -- Exert( ... ) 
const int ntpb = 1024;
const int STREAMS = 32;

void check(cudaError_t error) {
	if (error != cudaSuccess) {
		throw std::exception(cudaGetErrorString(error));
	}
}

struct SImageData
{
	SImageData()
		: m_width(0)
		, m_height(0)
	{ }

	long m_width;
	long m_height;
	long m_pitch;
	std::vector<uint8_t> m_pixels;
};

float Gaussian(float sigma, float x)
{
	return expf(-(x*x) / (2.0f * sigma*sigma));
}

float GaussianSimpsonIntegration(float sigma, float a, float b)
{
	return
		((b - a) / 6.0f) *
		(Gaussian(sigma, a) + 4.0f * Gaussian(sigma, (a + b) / 2.0f) + Gaussian(sigma, b));
}

std::vector<float> GaussianKernelIntegrals(float sigma, int taps)
{
	std::vector<float> ret;
	float total = 0.0f;
	for (int i = 0; i < taps; ++i)
	{
		float x = float(i) - float(taps / 2);
		float value = GaussianSimpsonIntegration(sigma, x - 0.5f, x + 0.5f);
		ret.push_back(value);
		total += value;
	}
	// normalize it
	for (unsigned int i = 0; i < ret.size(); ++i)
	{
		ret[i] /= total;
	}
	return ret;
}

struct BGRPixel {
	float b;
	float g;
	float r;
};

__global__ void blur_kernel(BGRPixel* imageIn, BGRPixel* imageOut, float* blur, int n_blur, int x, int start, int jump) {
	int idx = blockDim.x*blockIdx.x + threadIdx.x;	// Location on the row

	if (idx < x) {
		int id = start + idx;
		int bstart = id - (n_blur / 2)*jump;

		BGRPixel pixel{ 0.0f, 0.0f, 0.0f };

		for (int i = 0; i < n_blur; ++i) {
			int bid = bstart + i*jump;
			float iblur = blur[i];

			pixel.b += imageIn[bid].b * iblur;
			pixel.g += imageIn[bid].g * iblur;
			pixel.r += imageIn[bid].r * iblur;
		}

		imageOut[id].b = pixel.b;
		imageOut[id].g = pixel.g;
		imageOut[id].r = pixel.r;
	}
}

void BlurImage(const SImageData& srcImage, SImageData &destImage, float xblursigma, float yblursigma, unsigned int xblursize, unsigned int yblursize)
{
	int xImage = srcImage.m_width;							// Width of image
	int yImage = srcImage.m_height;							// Height of image
	int imageSize = xImage*yImage;

	int xPadded = xImage + (xblursize - 1);					// Width including padding
	int yPadded = yImage + (yblursize - 1);					// Height including padding
	int paddedSize = xPadded*yPadded;

	int xPad = xblursize / 2;								// Number of padding columns on each side
	int yPad = yblursize / 2;
	int padOffset = xPadded*yPad + xPad;							// Offset to first pixel in padded image

	float* pinnedImage = nullptr;
	BGRPixel* d_padded1 = nullptr;
	BGRPixel* d_padded2 = nullptr;

	float*	d_xblur = nullptr;					// XBlur integrals
	int		n_xblur;							// N

	float*	d_yblur = nullptr;					// YBlur integrals
	int		n_yblur;							// N

	// Allocate memory for host and device
	check(cudaHostAlloc((void**)&pinnedImage, 3 * imageSize * sizeof(float), 0));
	check(cudaMalloc((void**)&d_padded1, paddedSize * sizeof(BGRPixel)));
	check(cudaMalloc((void**)&d_padded2, paddedSize * sizeof(BGRPixel)));

	// Copy image to pinned memory
	for (int i = 0; i < 3 * imageSize; ++i) {
		pinnedImage[i] = (float)srcImage.m_pixels[i];
	}

	// Allocate and assign intergrals
	{
		auto row_blur = GaussianKernelIntegrals(xblursigma, xblursize);
		auto col_blur = GaussianKernelIntegrals(yblursigma, yblursize);

		// ROW
		n_xblur = row_blur.size();
		check(cudaMalloc((void**)&d_xblur, n_xblur * sizeof(float)));
		check(cudaMemcpy(d_xblur, row_blur.data(), n_xblur * sizeof(float), cudaMemcpyHostToDevice));

		// COLUMN
		n_yblur = col_blur.size();
		check(cudaMalloc((void**)&d_yblur, n_yblur * sizeof(float)));
		check(cudaMemcpy(d_yblur, col_blur.data(), n_yblur * sizeof(float), cudaMemcpyHostToDevice));
	}


	cudaStream_t stream[STREAMS];

	int nblks = (xImage + (ntpb - 1)) / ntpb;

	for (int i = 0; i < STREAMS; ++i) {
		check(cudaStreamCreate(&stream[i]));
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			cudaMemcpyAsync(d_padded1 + padOffset + i*xPadded, pinnedImage + (3 * i*xImage), 3 * xImage * sizeof(float), cudaMemcpyHostToDevice, stream[j]);
		}
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded1, d_padded2, d_xblur, n_xblur, xImage, padOffset + i*xPadded, 1);
		}
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			blur_kernel << <nblks, ntpb, 0, stream[j] >> > (d_padded2, d_padded1, d_yblur, n_yblur, xImage, padOffset + i*xPadded, xPadded);
		}
	}

	for (int i = 0; i < yImage;) {
		for (int j = 0; j < STREAMS && i < yImage; ++j, ++i) {
			check(cudaMemcpyAsync(pinnedImage + (3 * i*xImage), d_padded1 + padOffset + i*xPadded, xImage * sizeof(BGRPixel), cudaMemcpyDeviceToHost, stream[j]));
		}
	}

	for (int i = 0; i < STREAMS; ++i) {
		check(cudaStreamSynchronize(stream[i]));
		check(cudaStreamDestroy(stream[i]));
	}

	destImage.m_width = srcImage.m_width;
	destImage.m_height = srcImage.m_height;
	destImage.m_pitch = srcImage.m_pitch;
	destImage.m_pixels.resize(srcImage.m_pixels.size());

	for (int i = 0; i < 3 * imageSize; i++) {
		destImage.m_pixels[i] = (uint8_t)pinnedImage[i];
	};

	check(cudaFree(d_xblur));
	check(cudaFree(d_yblur));

	check(cudaFreeHost(pinnedImage));
	check(cudaFree(d_padded1));
	check(cudaFree(d_padded2));

	check(cudaDeviceReset());
}

Results

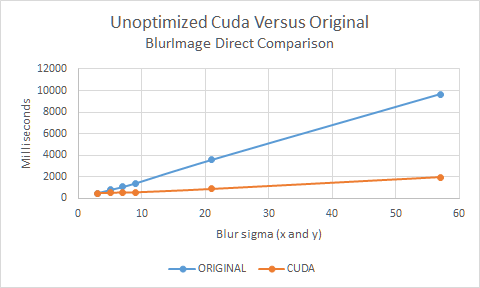
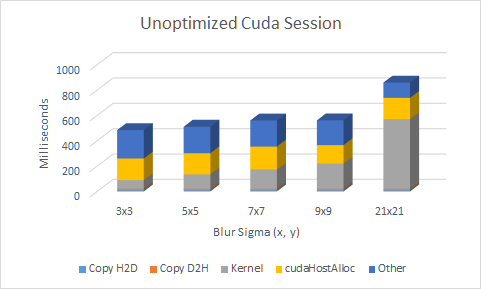
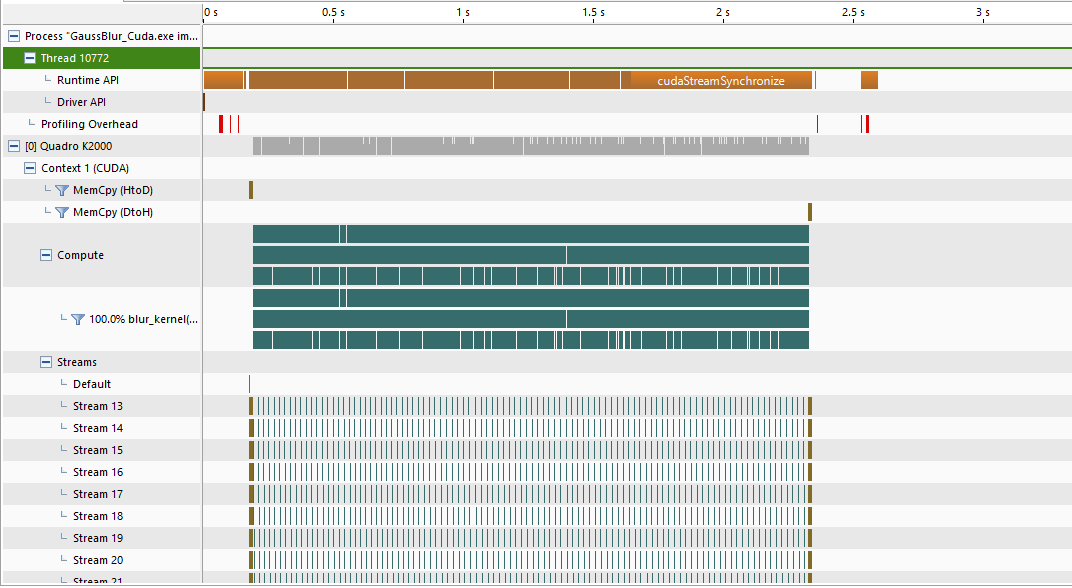
Obtained using Quadro K620
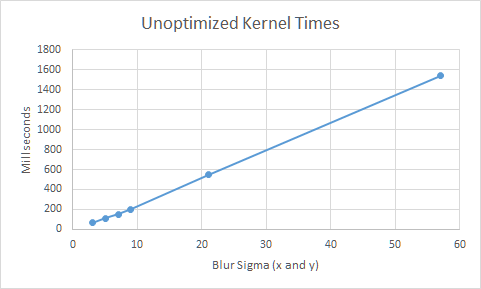
Uvso2.png Usession.png Ktimes.png
Using a Quadro K2000
Streams.png

Output Images

Image Gallery 135MB Image 135MB 3x3 Result

Mandelbrot

[Expand] Unoptimized - Mandelbrot( ... ) 
//C++ Includes
#include <iostream>
#include <complex>
#include <vector>
#include <chrono>
#include <functional>
#include <cuda_runtime.h>

//CUDA Complex Numbers
#include <cuComplex.h>

//Helper Includes
#include "window.h"
#include "save_image.h"
#include "utils.h"

const int ntpb = 32;

//Compute Color for each pixel
__global__ void computeMandelbrot(  int iter_max, int* d_colors, 
                                    int fract_width, int fract_height, 
                                    int scr_width, int scr_height, 
                                    int fract_xmin, int fract_ymin){
                                        
    int row = blockIdx.y * blockDim.y + threadIdx.y;    //Row
    int col = blockIdx.x * blockDim.x + threadIdx.x;    //Col

    int idx = row * scr_width + col;                    //Pixel Index

    if(col < scr_width && row < scr_height){

        //Use Floating Complex Numbers to calculate color for each pixel
        int result = 0;
        cuFloatComplex c = make_cuFloatComplex((float)col, (float)row);
        cuFloatComplex d = make_cuFloatComplex(cuCrealf(c) / (float)scr_width * fract_width + fract_xmin , cuCimagf(c) / (float)scr_height * fract_height + fract_ymin);
        cuFloatComplex z = make_cuFloatComplex(0.0f, 0.0f);

        while((cuCabsf(z) < 2.0f) && (result < iter_max)){
            z = (cuCaddf(cuCmulf(z,z),d));
            result++;
        }
        d_colors[idx] = result;                         //Output
    }
}

void mandelbrot(){
    window<int> scr(0, 1000, 0, 1000);              //Image Size
    window<float> fract(-2.2,1.2,-1.7,1.7);         //Fractal Size
    int iter_max = 500;                             //Iterations
    const char* fname = "mandlebrot_gpu.png";       //Output File Name
    bool smooth_color = true;                       //Color Smoothing

    int nblks = (scr.width() + ntpb - 1)/ ntpb;     //Blocks
    std::vector<int> colors(scr.size());            //Output Vector
    
    //Allocate Device Memory
    int* d_colors;                                  
    cudaMalloc((void**)&d_colors, scr.size() * sizeof(int));

    //Grid Layout
    dim3 dGrid(nblks, nblks);
    dim3 dBlock(ntpb, ntpb);

    //Execute Kernel
    auto start = std::chrono::steady_clock::now();
    computeMandelbrot<<<dGrid, dBlock>>>(iter_max, d_colors, fract.width(), fract.height(), scr.width(), scr.height(), fract.x_min(), fract.y_min());
    cudaDeviceSynchronize();
    auto end = std::chrono::steady_clock::now();

    //Output Time
    std::cout << "Time to generate " << fname << " = " << std::chrono::duration <float, std::milli> (end - start).count() << " [ms]" << std::endl;

    //Copy Data back to Host
    cudaMemcpy(colors.data(), d_colors, scr.size() * sizeof(int), cudaMemcpyDeviceToHost);

    //Plot Data and Free Memory
    plot(scr, colors, iter_max, fname, smooth_color);
    cudaFree(d_colors);
}

int main(){
    mandelbrot();
    return 0;
}

Objectives

The main objective was refactor the get_number_iterations() function and the subsequent functions called that created the nested loops. The objective was met as all the functions were refactored into a single device function that did the calculation for a single pixel of the image. As the original program was done with doubles, all of the doubles were changed to floats.

Steps

Host Memory Management

No changes were needed to the Host Memory as no data is copied from the host to the device. The vector on the host that contains the data was not changed and data from the device was copied to this vector to be output the plot file.

Device Memory Management

Only a single array to hold the value for each pixel was created on the device. This array has a size of image width * image height and the row and columns for each image are calculated from this which are used in the complex number calculations along with the values that specify the parameters of the fractal.

Kernels

The three functions from the original code ( get_number_iterations() , escape() and scale() were refactored into a single computeMandelbrot() function. The device kernel calculates the row and column for the pixel and then uses the row and colmn values along with the picture width and fractal parameters to calculate the value. Complex floating point numbers are used using the cuComplex.h header file which also includes the operations for the complex numbers as well. As threads are not reliant on each other for any data, no use of __syncthreads() is required. As threads complete computing the values, they output the value to the d_colors array.

Device to Host

After that is done the image is copied back using a single memcpy to the host.

Results

The program was compiled using clang++ , icpc (Intel Parallel Studio Compiler) and NVCC for the GPU. Runtimes for the standard clang++ version were extremely slow as the size of the resultant image increased. Compiling the program using the icpc compiler brought in significant changes without modifying any code and reduced runtimes drastically for running purely on a CPU. Using the parallel version based on CUDA improved the runtime massively over the clang++ compiled version and even the icpc version as more values could be calculated in parallel. 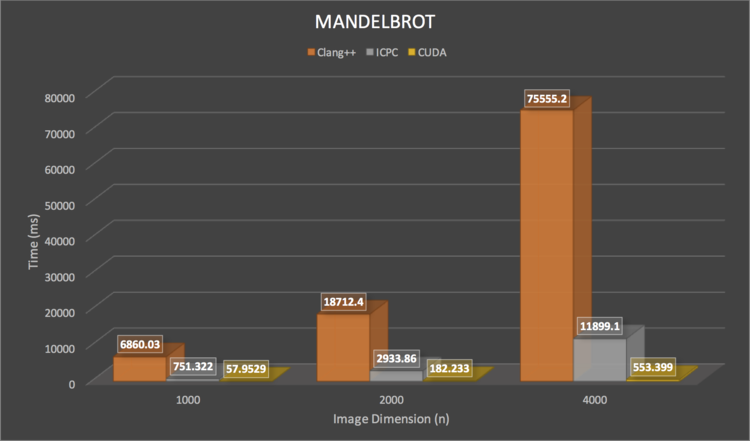Mandelbrot.png

Output Images

Image Output

Future Optimizations

As there isn't any data intensive tasks in this program, further optimizations would include creating streams of kernels and having them execute concurrently in order to improve runtime of the current solution.

Retrieved from "https://wiki.cdot.senecapolytechnic.ca/w/index.php?title=BETTERRED&oldid=125676"