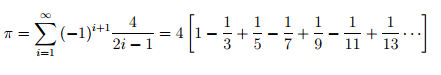Difference between revisions of "Dev/null"
(→Assignment 2) |
(→Team Members) |
||
| Line 2: | Line 2: | ||
= /dev/null = | = /dev/null = | ||
== Team Members == | == Team Members == | ||
| − | # [mailto:yjghitisduque@senecacollege.ca?subject=gpu610 Yehoshua Ghitis], | + | # [mailto:yjghitisduque@senecacollege.ca?subject=gpu610 Yehoshua Ghitis], Text search |
# [mailto:bbershadsky@myseneca.ca?subject=gpu610 Boris Bershadsky], Prime generator | # [mailto:bbershadsky@myseneca.ca?subject=gpu610 Boris Bershadsky], Prime generator | ||
# [mailto:oaislam1@myseneca.ca?subject=gpu610 Ozal Islam], Precision of Pi | # [mailto:oaislam1@myseneca.ca?subject=gpu610 Ozal Islam], Precision of Pi | ||
Latest revision as of 16:46, 15 December 2015
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
/dev/null
Team Members
- Yehoshua Ghitis, Text search
- Boris Bershadsky, Prime generator
- Ozal Islam, Precision of Pi
oaislam1@myseneca.ca, bbershadsky@myseneca.ca?subject=dps901-gpu610 Email All
Progress
Assignment 1
Precision of Pi
The number of miliseconds required to complete the function for computing the precision of Pi takes longer if the number of iterations is increased by 10 exponentially.
If GPU was used to compute the function then the number of miliseconds could be drastically reduced with high number of iterations.
Test runs with number of iterations:
oaislam1@matrix:~/Ozal/GPU610/a1> time a1 100 Compute pi - took - 0 millisecs 3.131592903558551910236928961239755153656005859375 real 0m0.137s user 0m0.004s sys 0m0.008s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 5000 Compute pi - took - 0 millisecs 3.14139265359178754266622490831650793552398681640625 real 0m0.145s user 0m0.004s sys 0m0.004s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 10000 Compute pi - took - 1 millisecs 3.141492653590030936783250581356696784496307373046875 real 0m0.143s user 0m0.000s sys 0m0.012s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 100000 Compute pi - took - 12 millisecs 3.14158265358971622305261917063035070896148681640625 real 0m0.141s user 0m0.012s sys 0m0.012s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 1000000 Compute pi - took - 139 millisecs 3.141591653589779209454491137876175343990325927734375 real 0m0.269s user 0m0.140s sys 0m0.008s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 1000000000 Compute pi - took - 178576 millisecs 3.14159265258789854868837210233323276042938232421875 real 2m58.717s user 2m58.315s sys 0m0.040s
Sample GProf profile:
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 100.00 10.05 10.05 compute_pi(int) 0.00 10.05 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10compute_pii
Calculation of prime numbers
Prime numbers are essential in the science of cryptography and are a good test of computational capacity of computers. The bigger the number, the more exponentially the hardware must work to calculate the next prime number.
Calculation of prime numbers is a very simple objective with a simple double for loop:
for (int i = 2; i<100; i++)
for (int j = 2; j*j <= i; j++)
{
if (i % j == 0)
break;
else if (j + 1 > sqrt(i)) {
std::cout << i << " ";
}
}
However, this serial processing is extremely inefficient when the numbers become extremely large. For the range of 1-1,000,000 the results are as follows:
real 0m4.982s user 0m3.644s sys 0m0.072s
Flat profile:
Each sample counts as 0.01 seconds.
% cumulative self self total time seconds seconds calls Ts/call Ts/call name
100.00 3.63 3.63 genPrime(unsigned long long, unsigned long long)
0.00 3.63 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z8genPrimeyy
There are 78496 prime numbers in the calculated range. Splitting the for loop between several cores to handle each subrange separately can yield extremely high performance gains.
Console output:
\\CPD S4\GPU610\a1\a1Boris\Debug>a1Boris 5000
- Team /dev/null GPU610 PRIME NUMBER GENERATOR***
No range given (or bad input), using preset values Generating from range (0~5000)
5 7 11 13 17 19 23 29 31
37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233
String search
A simple program that searches for a string inside a text file and prints every line where it is found.
./find kari text.txt no half-tones, but using techniques called meri and kari, in which the blowing The string kari was found in the file text.txt at line 6 and column 52 ./find is text.txt which is called a "fipple"—and thus has limited pitch control, the shakuhachi The string is was found in the file text.txt at line 2 and column 6 angle is adjusted to bend the pitch downward and upward, respectively, The string is was found in the file text.txt at line 7 and column 6 ./find is text.txt which is called a "fipple"—and thus has limited pitch control, the shakuhachi The string is was found in the file text.txt at line 2 and column 6 angle is adjusted to bend the pitch downward and upward, respectively, The string is was found in the file text.txt at line 7 and column 6 yjghitisduque@matrix:~/c++/GPUA1> ./find is text.txt text2.txt which is called a "fipple"—and thus has limited pitch control, the shakuhachi The string is was found in the file text.txt at line 2 and column 6 angle is adjusted to bend the pitch downward and upward, respectively, The string is was found in the file text.txt at line 7 and column 6 which is called a "fipple"—and thus The string is was found in the file text2.txt at line 3 and column 6 angle is adjusted to bend the pitch The string is was found in the file text2.txt at line 13 and column 6
The increase in time spent searching is linear and depends on the size of the file or files. This can take much longer when it comes to extremely large files.
Assignment 2
https://github.com/bbershadsky/GPU610-a2 Still writing code to parallelize the process