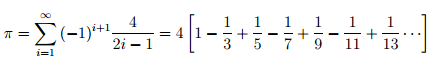Difference between revisions of "Dev/null"
Ozal Islam (talk | contribs) (→Precision of Pi) |
(→Assignment 1) |
||
| Line 77: | Line 77: | ||
100.00 10.05 10.05 compute_pi(int) | 100.00 10.05 10.05 compute_pi(int) | ||
0.00 10.05 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10compute_pii</pre> | 0.00 10.05 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10compute_pii</pre> | ||
| + | |||
| + | |||
| + | ==== Calculation of prime numbers ==== | ||
| + | |||
| + | Prime numbers are essential in the science of cryptography and are a good test of computational capacity of computers. The bigger the number, the more exponentially the hardware must work to calculate the next prime number. | ||
| + | |||
| + | Calculation of prime numbers is a very simple objective with a simple double for loop: | ||
| + | |||
| + | |||
| + | for (int i = 2; i<100; i++) | ||
| + | for (int j = 2; j*j <= i; j++) | ||
| + | { | ||
| + | if (i % j == 0) | ||
| + | break; | ||
| + | else if (j + 1 > sqrt(i)) { | ||
| + | std::cout << i << " "; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | |||
| + | However, this serial processing is extremely inefficient when the numbers become extremely large. For the range of 1-1,000,000 the results are as follows: | ||
| + | |||
| + | real 0m4.982s | ||
| + | user 0m3.644s | ||
| + | sys 0m0.072s | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Flat profile: | ||
| + | |||
| + | Each sample counts as 0.01 seconds. | ||
| + | % cumulative self self total | ||
| + | time seconds seconds calls Ts/call Ts/call name | ||
| + | 100.00 3.63 3.63 genPrime(unsigned long long, unsigned long long) | ||
| + | 0.00 3.63 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z8genPrimeyy | ||
| + | |||
| + | |||
| + | |||
| + | There are 78496 prime numbers in the calculated range. Splitting the for loop between several cores to handle each subrange separately can yield extremely high performance gains. | ||
| + | |||
| + | Console output: | ||
| + | |||
| + | |||
| + | \\CPD S4\GPU610\a1\a1Boris\Debug>a1Boris 5000 | ||
| + | ***Team /dev/null GPU610 PRIME NUMBER GENERATOR*** | ||
| + | No range given (or bad input), using preset values | ||
| + | Generating from range (0~5000) | ||
| + | -------------------------------------------------------------------------------- | ||
| + | 5 7 11 13 17 19 23 29 31 | ||
| + | 37 41 43 47 53 59 61 67 71 73 | ||
| + | 79 83 89 97 101 103 107 109 113 127 | ||
| + | 131 137 139 149 151 157 163 167 173 179 | ||
| + | 181 191 193 197 199 211 223 227 229 233 | ||
=== Assignment 2 === | === Assignment 2 === | ||
=== Assignment 3 === | === Assignment 3 === | ||
Revision as of 22:28, 14 October 2015
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Contents
/dev/null
Team Members
- Yehoshua Ghitis, Stuff
- Boris Bershadsky, Prime generator
- Ozal Islam, Precision of Pi
oaislam1@myseneca.ca, bbershadsky@myseneca.ca?subject=dps901-gpu610 Email All
Progress
Assignment 1
Precision of Pi
The number of miliseconds required to complete the function for computing the precision of Pi takes longer if the number of iterations is increased by 10 exponentially.
If GPU was used to compute the function then the number of miliseconds could be drastically reduced with high number of iterations.
Test runs with number of iterations:
oaislam1@matrix:~/Ozal/GPU610/a1> time a1 100 Compute pi - took - 0 millisecs 3.131592903558551910236928961239755153656005859375 real 0m0.137s user 0m0.004s sys 0m0.008s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 5000 Compute pi - took - 0 millisecs 3.14139265359178754266622490831650793552398681640625 real 0m0.145s user 0m0.004s sys 0m0.004s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 10000 Compute pi - took - 1 millisecs 3.141492653590030936783250581356696784496307373046875 real 0m0.143s user 0m0.000s sys 0m0.012s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 100000 Compute pi - took - 12 millisecs 3.14158265358971622305261917063035070896148681640625 real 0m0.141s user 0m0.012s sys 0m0.012s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 1000000 Compute pi - took - 139 millisecs 3.141591653589779209454491137876175343990325927734375 real 0m0.269s user 0m0.140s sys 0m0.008s oaislam1@matrix:~/Ozal/GPU610/a1> time a1 1000000000 Compute pi - took - 178576 millisecs 3.14159265258789854868837210233323276042938232421875 real 2m58.717s user 2m58.315s sys 0m0.040s
Sample GProf profile:
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls Ts/call Ts/call name 100.00 10.05 10.05 compute_pi(int) 0.00 10.05 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z10compute_pii
Calculation of prime numbers
Prime numbers are essential in the science of cryptography and are a good test of computational capacity of computers. The bigger the number, the more exponentially the hardware must work to calculate the next prime number.
Calculation of prime numbers is a very simple objective with a simple double for loop:
for (int i = 2; i<100; i++)
for (int j = 2; j*j <= i; j++)
{
if (i % j == 0)
break;
else if (j + 1 > sqrt(i)) {
std::cout << i << " ";
}
}
However, this serial processing is extremely inefficient when the numbers become extremely large. For the range of 1-1,000,000 the results are as follows:
real 0m4.982s user 0m3.644s sys 0m0.072s
Flat profile:
Each sample counts as 0.01 seconds.
% cumulative self self total time seconds seconds calls Ts/call Ts/call name
100.00 3.63 3.63 genPrime(unsigned long long, unsigned long long)
0.00 3.63 0.00 1 0.00 0.00 _GLOBAL__sub_I__Z8genPrimeyy
There are 78496 prime numbers in the calculated range. Splitting the for loop between several cores to handle each subrange separately can yield extremely high performance gains.
Console output:
\\CPD S4\GPU610\a1\a1Boris\Debug>a1Boris 5000
- Team /dev/null GPU610 PRIME NUMBER GENERATOR***
No range given (or bad input), using preset values Generating from range (0~5000)
5 7 11 13 17 19 23 29 31
37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233