Difference between revisions of "Skynet/GPU610"
(changed heading to make selection seem more apparent) |
|||
| Line 1: | Line 1: | ||
{{GPU610/DPS915 Index | 20143}} | {{GPU610/DPS915 Index | 20143}} | ||
Team Pages: [[Skynet/GPU610|GPU610]] | [[Skynet/GAM531|GAM531]] | Team Pages: [[Skynet/GPU610|GPU610]] | [[Skynet/GAM531|GAM531]] | ||
| − | = Ray Tracer | + | = Selected Program = |
| + | Ray Tracer | ||
== Team Members == | == Team Members == | ||
# [mailto:mmwang2@myseneca.ca?subject=gpu610 Michael Wang], (responsibility tbd) | # [mailto:mmwang2@myseneca.ca?subject=gpu610 Michael Wang], (responsibility tbd) | ||
Revision as of 14:21, 6 October 2014
GPU610/DPS915 | Student List | Group and Project Index | Student Resources | Glossary
Team Pages: GPU610 | GAM531
Contents
Selected Program
Ray Tracer
Team Members
- Michael Wang, (responsibility tbd)
- Bruno Pereira, (responsibility tbd)
- ...
Progress
Assignment 1
Bruno
For assignment 1 I looked into finding a simple Ray Tracer that could be easily understood by someone with no image processing background and benefit from parallelization.
I found ray tracer that matched the criteria I was looking for at http://scratchapixel.com/assets/Uploads/Lesson001/Source%20Code/raytracer.cpp
Looking into Big O notation I believe this program falls under [f(n) = n ^ 2]
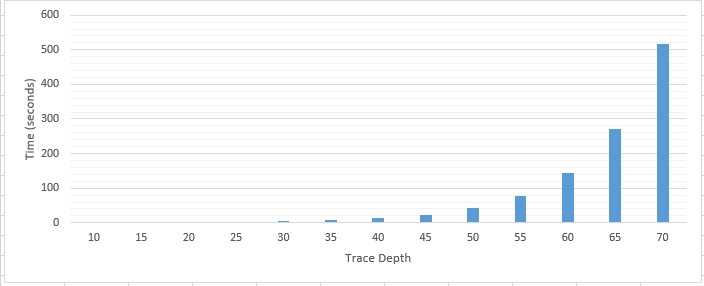
I profiled the ray tracer by modifying trace depths, as seen below:
Depth of 70
Each sample counts as 0.01 seconds.
% cumulative self self total time seconds seconds calls ms/call ms/call name 99.99 517.97 517.97 307200 1.69 1.69 Vec3<float> trace<float>(Vec3<float> const&, Vec3<float> const&, std::vector<Sphere<float>*, std::allocator<Sphere<float>*> > const&, int const&) 0.01 518.00 0.03 void render<float>(std::vector<Sphere<float>*, std::allocator<Sphere<float>*> > const&) 0.00 518.00 0.00 1 0.00 0.00 _GLOBAL__sub_I_main
The program spends nearly 100% of all processing with in its Vec3 trace method, this is a recursive method.
Vec3<T> trace(const Vec3<T> &rayorig, const Vec3<T> &raydir,const std::vector<Sphere<T> *> &spheres, const int &depth)
.......
.......
if ((sphere->transparency > 0 || sphere->reflection > 0) && depth < MAX_RAY_DEPTH) {
T facingratio = -raydir.dot(nhit);
// change the mix value to tweak the effect
T fresneleffect = mix<T>(pow(1 - facingratio, 3), 1, 0.1);
Vec3<T> refldir = raydir - nhit * 2 * raydir.dot(nhit);
refldir.normalize();
Vec3<T> reflection = trace(phit + nhit * bias, refldir, spheres, depth + 1);
Vec3<T> refraction = 0;
if (sphere->transparency) {
T ior = 1.1, eta = (inside) ? ior : 1 / ior;
T cosi = -nhit.dot(raydir);
T k = 1 - eta * eta * (1 - cosi * cosi);
Vec3<T> refrdir = raydir * eta + nhit * (eta * cosi - sqrt(k));
refrdir.normalize();
refraction = trace(phit - nhit * bias, refrdir, spheres, depth + 1);
}
surfaceColor = (reflection * fresneleffect + refraction * (1 - fresneleffect) * sphere->transparency) * sphere->surfaceColor;
}
...
...
void render(const std::vector<Sphere<T> *> &spheres)
{
unsigned width = 640, height = 480;
Vec3<T> *image = new Vec3<T>[width * height], *pixel = image;
T invWidth = 1 / T(width), invHeight = 1 / T(height);
T fov = 30, aspectratio = width / T(height);
T angle = tan(M_PI * 0.5 * fov / T(180));
// Trace rays
for (unsigned y = 0; y < height; ++y) {
for (unsigned x = 0; x < width; ++x, ++pixel) {
T xx = (2 * ((x + 0.5) * invWidth) - 1) * angle * aspectratio;
T yy = (1 - 2 * ((y + 0.5) * invHeight)) * angle;
Vec3<T> raydir(xx, yy, -1);
raydir.normalize();
*pixel = trace(Vec3<T>(0), raydir, spheres, 0);
}
}
Michael
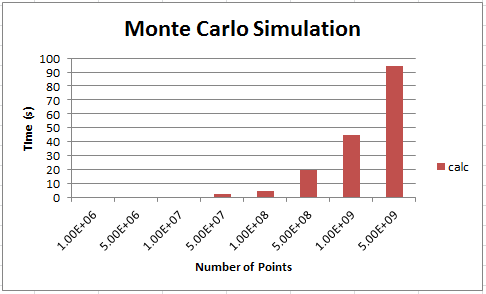
I have picked the Monte Carlo simulation for this assignment. Source code was from here and was modified to take and argument as the number of iterations and factored out the function which is going to be used for parallelzation.
Runtime for this program O(N) and the results are as follows:
| N Iterations | Time (seconds) |
|---|---|
| 1,000,000 | 0.02 |
| 5,000,000 | 0.24 |
| 10,000,000 | 0.42 |
| 50,000,000 | 2.22 |
| 100,000,000 | 4.75 |
| 500,000,000 | 19.97 |
| 1,000,000,000 | 44.5 |
| 5,000,000,000 | 94.08 |
Due to the simplicity of the program, all of the time spent was on the calc function below, as iterations increased, the time it takes increases at a linear rate.
Function to parallelize:
void calc(int iterations, int* count){
double x, y, z;
for (int i=0;i<iterations;i++){
x = (double)rand()/RAND_MAX;
y = (double)rand()/RAND_MAX;
z = x*x+y*y;
if (z<=1){
(*count)++;
}
}
}